Примеры решения задач

Пример 1. Рассмотреть изменение продольных размеров квадрата, движущегося со скоростью v = 0,8 c вдоль одной из своих сторон.

Решение: При движении со скорость, близкой скорости света c продольные размеры квадрата будут изменяться так, что он превращается в прямоугольник. Форму прямоугольника можно оценить по углу  между его диагоналями arcctg = arcctg0,6;  59 .

Пример 2. Пусть энергия покоящегося тела равна Е. Найдите импульс этого тела в системе отсчета, движущегося со скоростью v.

Решение: В соответствии с формулами релятивистского преобразования 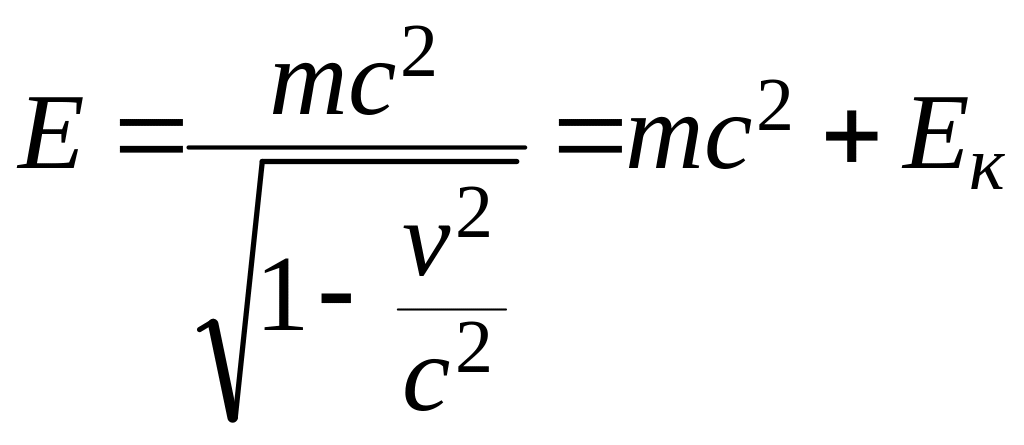импульс равен 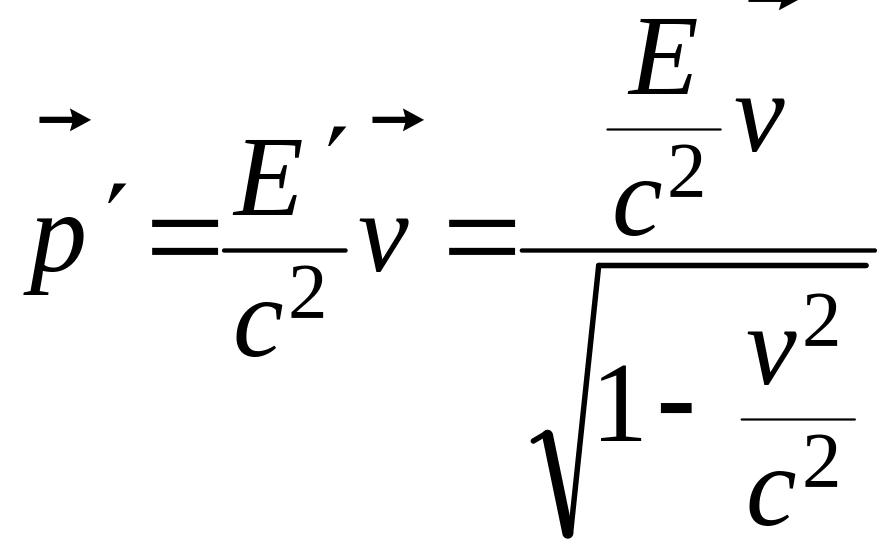. Видно, что получилась формула для релятивистского импульса с массой m = .

3 ГЛАВА
	КОЛЕБАНИЯ И ВОЛНЫ
		3.1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
		3.2. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
		3.3. ЗАТУХАЮЩИЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
		3.4. ВЫНУЖДЕННЫЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ. РЕЗОНАНС
		3.5. УПРУГИЕ ВОЛНЫ

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике: качание маятника часов, переменный электрический ток и т.д. Физическая природа колебаний может быть различной. В данном разделе будут рассмотрены механические колебания и процесс распространения механических колебаний в сплошной среде.

Цель главы – изучить характеристики и особенности различных видов механических колебаний: гармонических, свободных незатухающих, затухающих, вынужденных, закономерности распространения колебаний в сплошной среде

После изучения главы необходимо знать

• Определение и характеристики гармонических колебаний.

• Дифференциальное уравнение собственных гармонических колебаний и вид его решения.

• Пружинный, физический и математический маятник. Приведенная длина физического маятника

• Сложение одинаково направленных и взаимно перпендикулярных колебаний.

• Затухающие колебания. Дифференциальное уравнение затухающих колебаний и вид его решения. Логарифмический декремент затухания. Добротность.

• Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.

• Распространение волн в упругой среде. Продольные и поперечные волны. Скорость волн.

• Уравнение плоской и сферической волны. Волновое число.

• Интерференция волн. Стоячие волны.

• Энергия волны. Вектор Умова.

• Звуковые волны. Эффект Доплера.

3.1. Гармонические колебания

Колебанием (колебательным движением или процессом) называют изменение состояния колебательной системы (осциллятора), при котором значения физических величин (для механических колебаний, например, смещения, скорости, ускорения, для электрических колебаний - силы тока, напряжения), характеризующих состояние системы, меняются со временем по периодическому или почти периодическому закону.

Периодическим колебанием называют движение (процесс), если значения физических величин, изменяющихся в течение движения (процесса), повторяются через одинаковые промежутки времени.

Полным колебанием называют один законченный цикл колебательного движения (процесса), после которого оно повторяется в том же порядке.

Периодические колебания характеризуются периодом, частотой, амплитудой, фазой.

Периодом колебаний Т называется наименьший промежуток времени, через который колебательная система возвращается в произвольно выбранное исходное состояние (совершает одно полное колебание).

Частотой колебаний  называется величина, обратная периоду колебаний Т ( = ), равная числу полных колебаний в единицу времени и измеряемая в герцах (1 Гц соответствует одному колебанию в секунду).

Циклической или круговой частотой  называется величина, равная числу полных колебаний за время 2 секунд ( = 2 = ) и выражаемая в радианах на секунду (рад/с).

Амплитудой колебаний А называется наибольшее отклонение (от равновесного) значения колебательной величины.

Фазой колебаний  называется периодически изменяющийся во времени аргумент функции (которая описывает колебание), определяющий состояние колеблющейся системы в любой момент времени t. Начальная фаза колебаний ₀ характеризует состояние системы в момент времени t = 0.

Гармонические колебания – это простейшие периодические колебания, при которых колеблющаяся величина изменяется с течением времени по синусоидальному или косинусоидальному закону (рис. 3.1). Форма записи гармонических колебаний называется кинематическим уравнением гармонических колебаний:

x

Рис. 3.1

Рис. 3.1

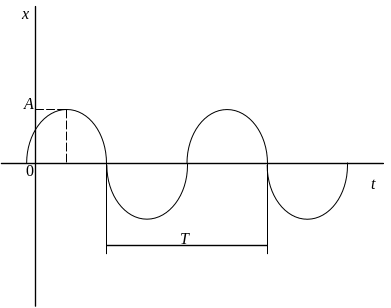
= Asin (t + ₀) = Acos(t + ₀ - ) = Acos(t + ₀'),

где х – значение колеблющейся величины в данный момент времени t (для механических колебаний х соответствует координате материальной точки) , А – амплитуда колебаний,  = t + ₀ – фаза колебаний, ₀ – начальная фаза синусоидального колебания, а ₀' = ₀ - – косинусоидального колебания.

Любое сложное периодическое колебание можно представить в виде суммы простейших гармонических колебаний (гармоник), которые не искажаются при воспроизведении.

Гармонические осцилляторы представляют собой идеализированные колебательные системы, в которых возникают собственные или свободные колебания за счет первоначально сообщенной им энергии, выводящей систему из равновесия, при последующем отсутствии каких - либо внешних воздействий.

Первая и вторая производные по времени от гармонически колеблющейся величины х = Acos(t + ₀' ) соответственно означают скорость и ускорение колеблющейся точки, они равны

v = = - Asin(t + ₀' ) = Acos(t + ₀' + ),

a = = - A²cos(t + ₀' ) = A²cos(t + ₀' + )

и совершают гармонические колебания с такой же частотой, но с амплитудами A и A², и со сдвигом по фазе на и , соответственно.

Дифференциальное уравнение гармонических колебаний. Если величина х изменяется по синусоидальному или косинусоидальному закону, то она удовлетворяет (является решением) дифференциальному уравнению гармонических колебаний вида:

+ ²х = 0.

С

Рис. 3.2

ложение гармонических колебаний. Кинематическое уравнение гармонических колебаний может быть получено при рассмотрении изменения во времени проекции на ось х радиуса-вектора величиной А, который равномерно вращается против часовой стрелки с постоянной угловой скоростью  от начального углового положения ₀ (в этом случае угол с осью х меняется по закону  = ₀ + t) (рис. 3.2).

Такой подход называется методом векторных диаграмм и он особенно удобен при сложении гармонических колебаний, так как позволяет сложение функций заменить наглядным сложением векторов (проекция суммы векторов равна сумме проекций).

При сложении, например, двух гармонических колебаний одного направления, одинаковой частоты, амплитуды которых равны А₁ и А₂, а начальные фазы - ₁ и ₂, получается гармоническое колебание такой же частоты, амплитуда А и начальная фаза ₀ которого могут быть найдены методом векторных диаграмм:

А² = А₁² + А₂² + 2А₁А₂cos(₂ - ₁),

tg₀ = (А₁sin₁ + А₂sin₂)/(А₁cos₁ + А₂cos₂).

Колебания называются когерентными, если разность фаз колебаний одинаковой частоты не меняется со временем. При ₂ - ₁ = ±2m амплитуда максимальна и равна А = А₁ + А₁, а при ₂ - ₁ = ±(2m + 1) - минимальна и равна А = |А₁ - А₂|.

Если точка движется по плоскости таким образом, что ее проекции на оси х и у совершают гармонические колебания, то говорят о сложении взаимно перпендикулярных гармонических колебаний. При сложении колебаний одинаковой частоты x = A₁cos(t + ₁) и у = A₂cos(t + ₂) траекторией точки является наклонный эллипс:

+ - cos(₂- ₁) = sin²(₂ - ₁).

Такое движение называется эллиптически поляризованными колебаниями. При ₂ - ₁= = оси эллипса совпадают с осями координат. При ₂ - ₁ = m эллипс вырождается в прямую. Такое движение называется линейно поляризованными колебаниями. При сложении взаимно перпендикулярных колебаний с различными, но кратными частотами результирующее движение происходит по траекториям, называемым фигурами Лиссажу. По виду фигуры Лиссажу можно установить отношение частот.

Примеры решения задач

Пример 1. Сформулировать зависимость полной энергии математического маятника от амплитуды малых собственных колебаний и частоты. Связать частоту колебаний с максимальной скоростью маятника.

Решение: Поскольку колебания малы, то тангенциальная составляющая возвращающей силы упругости , где малое смещение маятника от положения равновесия. Но это означает, что потенциальная энергия выражается формулой:

.

В крайней точке величина смещения маятника становится равной амплитудному значению смещения и, значит, в этой точке . Поскольку в крайней точке скорость маятника, а значит, и его кинетическая энергия равны нулю, то полная механическая энергия равна потенциальной: Е_мех = E_к + Е_п = . Поскольку при гармонических колебаниях смещения , то k = m². Но тогда = . В положении равновесия Е_п = 0 и Е_мех = Е_к. Поскольку энергия маятника не меняется (сопротивления нет и колебания собственные), то из того, что потенциальная энергия в крайней точке равна кинетической в равновесном (наинизшем) положении, следует = , откуда v_max = R или V = R, где V = v_max - амплитуда колебания скорости.

Пример 2. Какова начальная фаза гармонических колебаний скорости маятника, если v = v₀ при t = 0, а максимальная скорость равна V? Выразить результат через амплитуду смещения R и частоту колебаний . Каков ответ для случая нитяного маятника, колеблющегося под действием тяжести.

Решение: Для гармонических колебаний величины скорости имеем v = Vsin(t+₀). Для момента t = 0 имеем v₀ = Vsin₀, поэтому . Поскольку амплитудное (максимальное) значение скорости связано с амплитудой колебания смещения и частотой по формуле V = R, то . Для указанного в условии задачи маятника , а потому .