Самостоятельная работа студентов и контроль знаний студентов
Для успешного изучения курса общей физики необходимо регулярно самостоятельно работать над закреплением и углублением знаний. Основные знания, несомненно, дают книги. Предлагаемое пособие, в этом смысле, является путеводителем по обилию учебной, научной и методической литературы, накопленной библиотекой по данной дисциплине. Желательно при работе с пособием иметь под рукой ручку и блокнот.
После изучения каждого раздела необходимо проверить себя, ответив на вопросы для самоконтроля, помещенные в конце пособия. Возникающие затруднения следует преодолевать так: снова прочитать основной раздел в пособии, привлечь рекомендуемую основную и дополнительную литературу, отдохнуть и сделать перерыв, либо переключиться на другую дисциплину. Часто новое возвращение к «трудному» вопросу бывает более успешным.
Систематическая работа с разделами пособия поможет успешно отчитать лабораторную работу, а затем и сдать экзамен.
ГЛАВА |
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА |
1
В курсе общей физики приходится оперировать скалярными и векторными величинами. Поэтому прежде, чем приступить к изложению основных разделов физики, рассмотрим понятия о скалярных и векторных величинах, приведем краткие сведения из векторного анализа, позволяющие, в частности, производить действия над векторами.
Цель главы – усвоить понятия о скалярных и векторных величинах, научиться выполнять действия над векторами.
После изучения главы необходимо знать
Что такое скаляр?
Что такое вектор?
Сложение векторов.
Вычитание векторов.
Умножение вектора на скаляр.
Скалярное произведение векторов.
Векторное произведение.
Скалярно-векторное произведение
Двойное векторное произведение.
Величины, которые полностью определяются числовыми значениями, называются скалярными, или скалярами. Величины, характеризующиеся не только числовым значением, но и направлением в пространстве, называются векторными величинами, или векторами. Векторы на рисунках изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка в выбранном масштабе выражает числовое значение величины, а стрелка указывает направление величины в пространстве. Числовое значение вектора называют его длиной, или модулем. В тексте векторы принято обозначать жирными буквами или над буквами ставить стрелку, а модуль – той же буквой, но обычного шрифта. Действия над векторами подчиняются определенным закономерностям.
Сложение
и вычитание векторов.
Векторы могут быть отложены из любой
точки пространства. Возможен перенос
вектора параллельно себе без изменения
его направления. Суммой, например,
векторов
,
и
(составляющих векторов) называется
вектор
=
+
+
(результирующий
вектор), который соединяет начало первого
вектора с концом последнего вектора в
ломаной линии из составляющих векторов,
которые располагаются таким образом,
что к концу предыдущего составляющего
вектора пристраивается последующий в
любом порядке (правило многоугольника,
рис. 1.1). Разностью векторов
и
называется
такой вектор
=
-
=
+ (
-
),
который
в сумме с вектором
дает
вектор
=
+
(рис.
1.2).
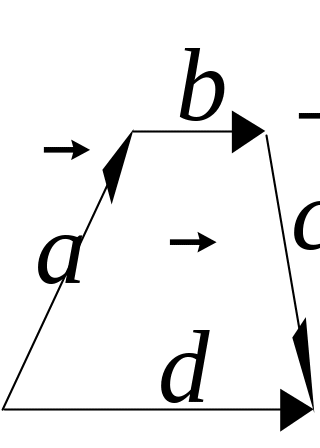
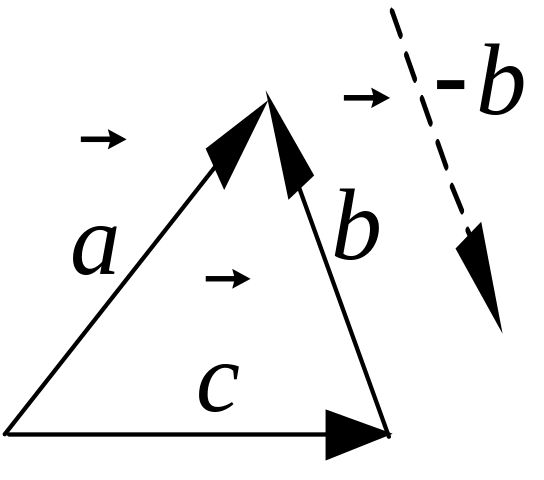
Рис. 1.1 Рис. 1.2
У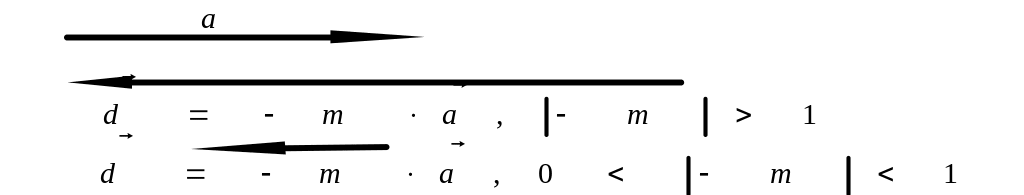
множение
вектора на скаляр.
Умножение вектора
на положительный скаляр n
дает вектор
=
n
того же направления, что и вектор
,
но в n
раз больше по величине (рис.1.3). Умножение
вектора
на отрицательный скаляр -m
дает вектор
=
-m
противоположного вектору
направления и в m
раз больший по величине (рис. 1.4). Операции
деления вектора на вектор не существует.
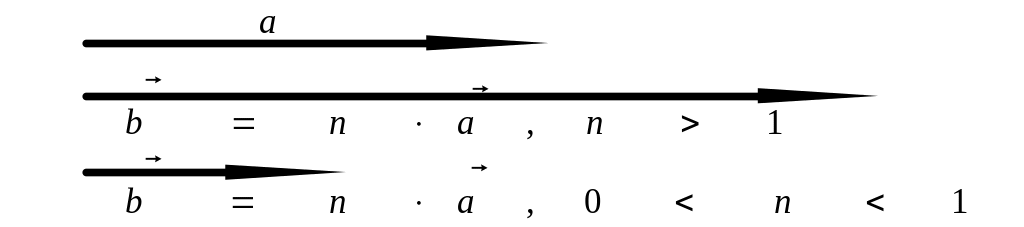
Рис. 1.3 Рис. 1.4
С
Рис.
1.6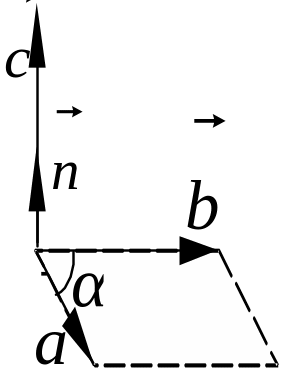
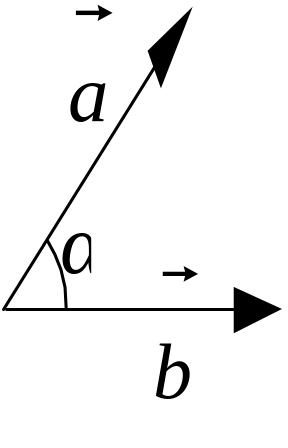Рис.
1.5
Векторное
произведение.
Векторным произведением векторов
и
называется
вектор
=
[
,
].
Его модуль равен произведению модулей
этих векторов на синус угла α между
ними: с
=
аbsinα
, а направление совпадает с нормальным
единичным вектором
к
плоскости, в которой лежат векторы
и
.
Направление вектора
определяется
по правилу правого винта, а векторы
,
и
образуют
правовинтовую систему (рис. 1.6). Перестановка
сомножителей вызывает изменение
направления результирующего вектора
на противоположное, так как векторное
произведение определяется направлением
вращения от первого сомножителя ко
второму: [
,
]
= - [
,
].
Векторы типа [ , ], направление которых связывается с направлением вращения, называются псевдовекторами (или аксиальными векторами). При изменении условия, например, при переходе от правой системы координат к левой, направления псевдовекторов изменяются на обратные, истинные же векторы при этом остаются без изменений. Векторное произведение будет псевдовектором, когда оба перемножаемых вектора являются истинными (или оба – псевдовекторы). Векторное произведение истинного вектора на псевдовектор будет истинным вектором.
Скалярно-векторное произведение. Скалярно-векторным произведением трех векторов называется выражение ( , [ , ]) = а(bcsinα)cosβ, равное скалярному произведению вектора на векторное произведение векторов и , где α - угол между векторами и , β - угол между вектором и нормальным единичным вектором , определяющим направление вектора [ , ]. Допускается циклическая перестановка сомножителей, откуда следует, что ( , [ , ]) = ( , [ , ]) = ( , [ , ]).
Двойное векторное произведение. Двойным векторным произведением трех векторов , и называется вектор = [ , [ , ]] перпендикулярный обоим сомножителям, поэтому вектор перпендикулярен к нормальному единичному вектору , определяющему направление вектора [ , ]. Вектор можно определить исходя из следующего соотношения:
[
Рис.
1.7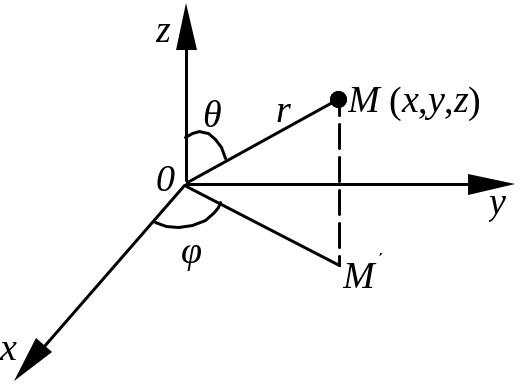
Радиус-вектор.
Радиусом-вектором r
некоторой точки М
(x,
y, z)
пространства называется вектор,
проведенный из начала координатной
системы О в данную точку М
(рис. 1.7). Как и любой вектор,
радиус-вектор можно выразить через его
проекции на оси координат rx,
ry,
rz
и единичные векторы (орты) этих осей
,
,
и
,
соответственно, в виде линейного
выражения:
=
rx
+
ry
+
rz
= x
+
y
+ z
,
где проекции на координатные оси можно приравнять декартовым координатам данной точки:
rx
= x,
ry
= y,
rz
= z.
Длина
радиуса-вектора
в
этом случае определяется из соотношения:
r2 = rx2 + ry 2 + rz2 = x2 + y2 + z2.
Производная функции. Дифференциалом (приращением) функции ƒ(t) называется выражение:
dƒ = ƒ′dt,
где ƒ′ - производная ƒ по t. Приращение функции за очень малый, но конечный промежуток времени Δt приближенно равно:
Δƒ
ƒ′Δt =
Δt
.
Аналогичную формулу можно написать и для любого вектора, который изменяется со временем по известному закону (t):
.
По
отношению к физическим векторным
величинам выражение
правильно будет рассматривать как
единое целое. В физике производная
выступает
как отношение достаточно малых, но
конечных приращений самой физической
величины d
(приращения
функции) и параметра dt
(приращения аргумента), а не как предел
этого отношения. Производные по времени
в физике иногда принято обозначать
символом соответствующей величины с
точкой над ним, например,
Производная скалярного произведения двух векторов (t) и (t) вычисляется по формуле:
Производная векторного произведения векторов (t) и (t) вычисляется по формуле:
Примеры решения задач
Пример 1.
Радиус-вектор частицы изменяется со
временем по закону:
= 5t2
+
4t
+
3
(м).
Найти скорость
и
ускорение
частицы.
Решение: Скорость равна первой производной радиуса-вектора по времени, откуда:
=
=
10t
+
4
(м/c).
Ускорение равно первой производной вектора скорости или второй производной радиуса-вектора по времени:
=
=
= 10
(м/с
).
Пример 2. Частица движется со скоростью = 3 + 4t + 9t2 (м/с). Найти перемещение частицы за первые 3 секунды ее движения.
Решение: Интегрированием находим изменение со временем радиуса-вектора частицы:
=
= 3t
+
2t2
+ 3t3
|
=
9
+ 18
+ 81
.
Таблица 1
Производные основных элементарных функций
|
|
|
|
с |
0 |
ln(x) |
1/x |
x |
1 |
sin(x) |
cos(x) |
xn |
nxn-1 |
cos(x) |
-sin(x) |
ex |
ex |
tg(x) |
1/cos2(x) |
ax |
axln(a) |
ctg(x) |
-1/sin2(x) |
Таблица 2