3.2. Свободные незатухающие механические колебания

В свободно колеблющейся системе, в которой не действуют силы трения (неконсервативные силы), колебания являются незатухающими, а сама колебательная система называется консервативной, так как в ней действуют только возвращающие консервативные силы (упругие силы, сила тяжести), направленные в сторону положения равновесия. Если отклонение консервативной механической системы из положения устойчивого равновесия описывается одним параметром (смещением х, углом отклонения , или углом закручивания φ), то при малых значениях данного параметра можно считать, что система совершает гармонические колебания. Примером гармонических колебаний могут служить малые колебания маятников (пружинного, крутильного, математического, физического).

Твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси, называется маятником.

Пружинным маятником называется тело массой m, совершающее прямолинейные гармонические колебания вдоль оси х под действием упругой силы F_упр = - kx. Уравнение движения пружинного маятника имеет такой же вид, как для груза на пружине:

F_упр = F = ma = m = - m²х = - kx 

- m Asin(t + ₀) = - kx  k = ,

где k – коэффициент упругости (эффективная жесткость), численно равный силе, вызывающей единичное смещение тела, определяемое выражением x = Asin(t + ₀). Циклическая частота и период колебаний имеют вид:

 = , T = 2 .

В общем случае, кинетическая энергия тела, колеблющегося под действием квазиупругой силы определяется уравнением

Е_к = = cos²(t + ₀),

а потенциальная энергия – уравнением

Е_п = = sin²(t + ₀).

С

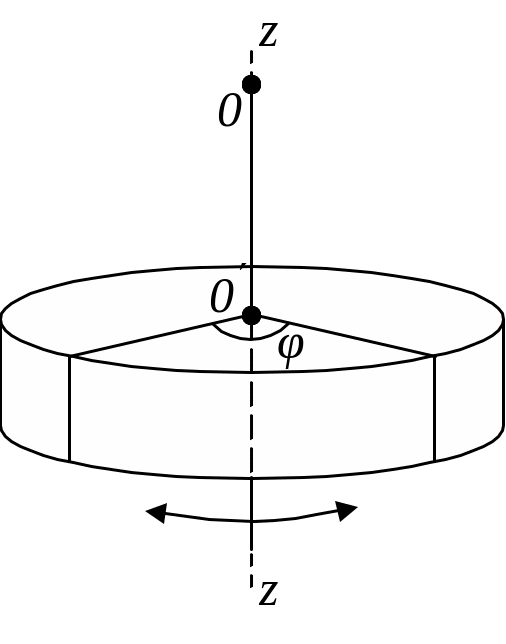Рис. 3.3

редняя кинетическая энергия равна средней потенциальной энергии. Полная механическая энергия системы, колеблющейся под действием упругой возвращаюшей консервативной силы, пропорциональна квадрату амплитуды

Е = Е_к + Е_п = [cos²(t + ₀) + sin²(t + ₀)] = .

Крутильным маятником называется тело, подвешенное на вертикальном невесомом стержне (нити) ОО, верхний конец которого закреплен неподвижно в точке О, совершающее крутильные колебания под действием упругих сил, возникающих в стержне при его закручивании вокруг оси z, совпадающей со стержнем и с одной из свободных осей вращения данного тела (рис. 3.3).

В случае гармонических колебаний при малых углах закручивания φ по закону Гука для деформации кручения момент закручивающей силы рассчитывается с помощью уравнения M = Dφ. При этом основное уравнение вращательного движения при кручении приобретает вид

М = - ε = -  = -  = Dφ,

откуда получается дифференциальное уравнение гармонических крутильных колебаний

-  - Dφ = 0  + φ = 0.

Циклическая частота и период колебаний крутильного маятника вычисляются по формулам:

 = , T = 2 .

Полная механическая энергия тела, совершающего крутильные колебания определяется из уравнения:

Е = Е_к + Е_п = ( + Dφ²),

где  - момент инерции тела, D – модуль кручения стержня.

М

Рис. 3.4

атематический маятник. Обычно под маятником понимают тело, которое колеблется в вертикальной плоскости под действием возвращающей консервативной силы - силы тяжести, и при этом ось маятника не проходит через центр тяжести тела. Простейший маятник состоит из груза массой m, размерами которого можно пренебречь по сравнению с длиной L нерастяжимой и невесомой нити. Такой маятник называется математическим и представляет собой материальную точку М массой m, колеблющуюся на неизменном расстоянии L от неподвижной точки подвеса О (рис. 3.4).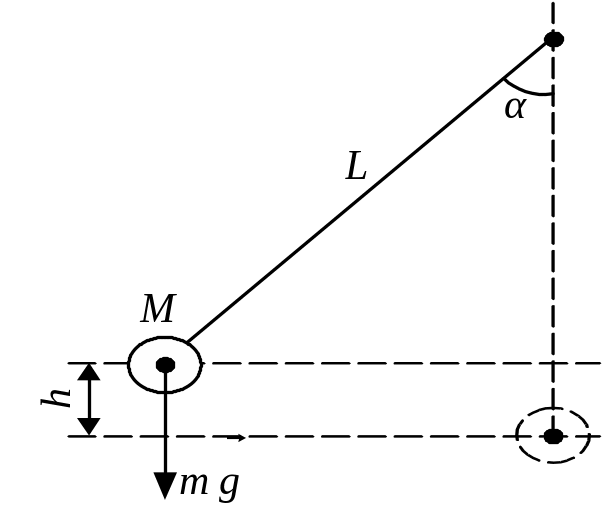

При малом угле отклонения  математического маятника от равновесного положения его колебания можно считать гармоническими

+ ω² = 0.

Момент инерции точки М относительно точки подвеса О равен  = mL². Кинетическая и потенциальная энергии точки М, совершающей колебательные движения, определяются с помощью уравнений:

Е_к = = mL² , Е_п = mgh = mgL(1–cos) = 2mgLsin² ≈ ,

где учитывается, что для малых колебаний sin ≈ .

Полная энергия математического маятника равна Е = Е_к + Е_п = .

После математических преобразований получается, что для малых углов  амплитуда колебаний А математического маятника определяется из соотношения вида

А² = 2L²²,

а циклическая частота и период колебаний по формулам, соответственно:

 = , T = 2 .

Уравнение колебаний математического маятника при этом принимает вид:

+  = 0.

Физический маятник

Ф

Рис. 3.5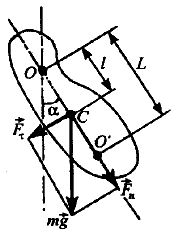

изическим маятником называется абсолютно твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр тяжести тела С.

Если физический маятник отклонен из положения равновесия на некоторый угол  (рис. 3.5), то момент возвращающей силы

M = Iε = I .