С другой стороны, при малых углах

М = F_l = -mglsin ≈ -mgl,

где I — момент инерции маятника относительно оси, проходящей через точку подвеса О, I - расстояние между точкой подвеса и центром тяжести С маятника, F_ = -mgsin - возвращающая сила.

Следовательно: I + mgl = 0, или

Таким образом, при малых колебаниях физический маятник совершает гармонические колебания  = ₀cos( ) с циклической частотой и периодом:

где длина называется приведенной длиной физического маятника.

Приведенная длина физического маятника — это длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник.

Точка О' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 3.5).

Математический маятник можно представить как частный (предельный) случай физического маятника, вся масса которого сосредоточена в его центре масс. При этом I = ml², следовательно Т = .

Гармонические колебания являются изохронными, то есть их период не зависит от амплитуды. Колебания большой амплитуды перестают быть гармоническими, а значит и изохронными – возникает зависимость периода от амплитуды.

Примеры решения задач

Пример 1. Нитяной маятник колеблется гармонично под действием силы тяжести. Как изменится амплитуда колебаний, если нить укоротить от l₁ до l₂, не меняя при этом энергии маятника?

Решение: Так как можно показать, что механическая энергия маятника равна Е = , то из условия задачи Е₁ = Е₂ следует = , и так как частота колебаний маятника , то = или = , откуда видно, что .

Пример 2. Лифт движется по вертикали сперва с ускорением а₁, а потом с «замедлением» а₂ в течение времени t₁ и t₂ соответственно. В лифте находится маятник длиной l. Сколько колебаний он сделает за время движения?

Решение: Число колебаний за время t = t₁ + t₂, будет равно N = N₁ + N₂. Можно показать, что в таком лифте периоды колебаний равны: Т₁ = и Т₂ = , поэтому получаем, что N = N₁ + N₂ = + .

3.3. Затухающие механические колебания

Е

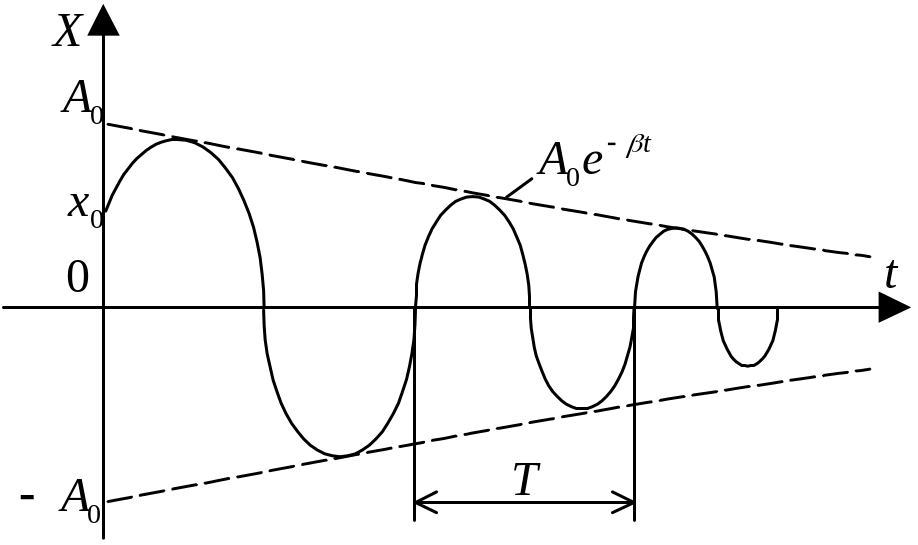Рис. 3.6

сли в колебательной системе происходят потери энергии, то амплитуда колебаний уменьшается со временем (рис. 3.6).

Затухающими колебаниями называются свободные колебания в диссипативной системе, на которую действуют неконсервативные силы (силы трения, сопротивления), в результате чего механическая энергия колебаний уменьшается с течением времени t. Если потери энергии механических колебаний определяются, например, силой вязкого трения, которая при малых скоростях пропорциональна скорости, то уравнение движения

m = - kx – b

приводится к линейному дифференциальному уравнению + 2 + ω₀²x = 0, которое называется уравнением затухающих колебаний. Здесь  = – коэффициент затухания, который обратен по величине такому промежутку времени  (время релаксации), за который амплитуда колебаний А уменьшается в e раз (то есть  = 1), ω₀ = – циклическая частота собственных колебаний в отсутствие затухания ( при   0).

Решение уравнения удобно искать в виде экспоненты: x(t) = A₀exp(-t) cos(ωt + φ₀), где ω = , а постоянные значения амплитуды собственных колебаний A и фазы колебаний φ (при t = 0) определяются начальными условиями. Амплитуда затухающих колебаний изменяется по закону А = A₀exp(-t). Период затухающих колебаний определяется по формуле

T = = .

Функция x (t) принимает нулевые значения через равные промежутки времени, поэтому ω и Т условно называют частотой и периодом затухающих колебаний. Если   ω₀ , то на каждом временном интервале Т    колебания можно считать гармоническими, а А(t) имеет смысл амплитуды колебаний на этом интервале. Поэтому А (t) называют (при любом слабом затухании   ω₀) зависящей от времени амплитудой затухающих колебаний. Убывание амплитуды за период Т, равное = exp(t), называют декрементом затухания, а логарифм декремента затухания называют логарифмическим декрементом затухания. Он равен

 = ln [ ] = T

Величина N_е = показывает, за сколько полных колебаний амплитуда уменьшается в е раз. Добротность колебательной системы определяется по формуле:

Q = 2 = = N_е =  ,

где Е – энергия системы в момент времени t, ∆Е – убыль энергии за один период колебания Т. Добротность Q системы тем выше, чем больше число колебаний N совершается, прежде чем амплитуда колебания А уменьшится в е раз.