Примеры решения задач

Пример 1. Тело движется вниз равноускоренно по наклонной плоскости, и зависимость пройденного пути от времени задается уравнением s = 2t + 2,1t². Найти коэффициент трения k тела о плоскость, если угол наклона плоскости к горизонту равен 45⁰.

Решение: Для нахождения k рассмотрим, под действием каких сил находится тело. На тело действуют силы: сила тяжести m , сила реакции опоры и сила .

Выберем систему координат так, чтобы ось ОХ была параллельна наклонной плоскости (рис. 2.15). Согласно второму закону Ньютона, проекция сил на оси:

Рис. 2.15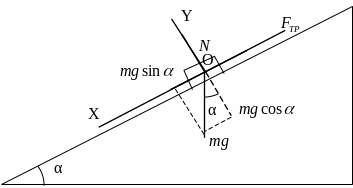

на ОY: mgcos = N;

на ОХ: ma = mgsin - mgkcos

Преобразовывая это выражение, можно найти коэффициент трения k:

.

Определим величину ускорения a:

4,2 (м/с²).

Подставив в формулу для k численное значение входящих в нее величин, получим значение коэффициента трения: k = 0,4.

Пример 2. Самолет движется со скоростью в горизонтальной плоскости, описывая окружность радиуса r. Определить: 1) на какой угол должен наклониться самолет при вираже; 2) какую перегрузку испытывает летчик.

Решение: В процессе виража на самолет (летчика) действует сила реакции воздуха = + и сила тяжести = m . Так как по вертикали ускорения самолета нет, то силы и уравновешивают друг друга. Сила сообщает самолету нормальное центростремительное ускорение. За угол наклона самолета принимается угол между векторами и . Перегрузка вычисляется как n = .

Получается, что можно записать следующие соотношения:

tg = , R_x = , R_у = mg

и, следовательно, tg = , откуда можно вычислить величину угла наклона .

Перегрузка определяется из уравнения

n = = .

2.4. Законы сохранения

Применение законов сохранения импульса, энергии и момента импульса необходимо когда законы взаимодействия тел неизвестны или описание поведения механической системы с помощью уравнений движения приводит к сложным соотношениям, в результате чего получить окончательное решение практически невозможно. Вместе с тем законы сохранения не могут дать однозначного ответа на вопрос о том, что происходит. Но если, исходя из каких-либо других соображений, можно указать, что именно должно произойти, то законы сохранения дают ответ на вопрос, как это произойдет.

Основной задачей механики является отыскание интегралов движения механической системы (совокупности тел), которые можно определить как постоянные при движении функции координат и скорости. Из множества интегралов движения системы выделяют три аддитивных интеграла движения (импульс, энергию и момент импульса), значение которых для замкнутой системы равно сумме значений для каждой части системы в отдельности.

Механическая система, на которую не действуют внешние силы или их равнодействующая равна нулю, называется замкнутой системой. Силы воздействия тел, не принадлежащих системе, называют внешними силами. Внутренние силы это силы взаимодействия тел механической системы.

Центром масс (центром инерции) системы материальных точек m₁,…, m_N называют точку, положение которой определяется радиус-вектором:

.

Связанную с центром масс поступательно движущуюся систему отсчета называют системой центра масс.

При рассмотрении относительного движения изолированной системы двух взаимодействующих материальных точек с массами m₁ и m₂ во внешнем потенциальном силовом поле вводится понятие материальной точки с приведенной массой μ определяемой из равенства:

.

Закон сохранения импульса (количества движения) вытекает из однородности пространства (равноправия всех его точек), для которого параллельный перенос системы в пространстве не изменяет ее механические свойства. Импульс системы определяется как сумма импульсов составляющих его частиц:

= ∑ .

Продифференцировав уравнение для радиуса-вектора по времени, найдем, что импульс системы выражается через скорость центра масс:

= m ,

где m – масса системы.

Просуммируем уравнение второго закона Ньютона = по всем точкам системы и учтем, что внутренние силы компенсируют друг друга:

= ∑ _внешн.

т.е. скорость изменения импульса системы равна результирующей внешних сил. Из данного уравнения следует, что импульс замкнутой системы сохраняется. Это вытекает из условия замкнутости системы, которое гласит, что сумма внешних сил, действующих на тела замкнутой системы, в любой момент времени равна нулю ∑ _внешн.dt = 0, что приводит к соотношению d = 0, из которого получается = const.

Импульс незамкнутой системы сохраняется в следующих случаях:

1. Если сумма внешних сил равна нулю.

2. Если результирующая внешняя сила перпендикулярна некоторому направлению, то сохраняется не вектор импульса системы, а проекция импульса системы на это направление.

3. Если взаимодействие продолжается очень короткое время, за которое изменением импульса системы можно пренебречь.

З

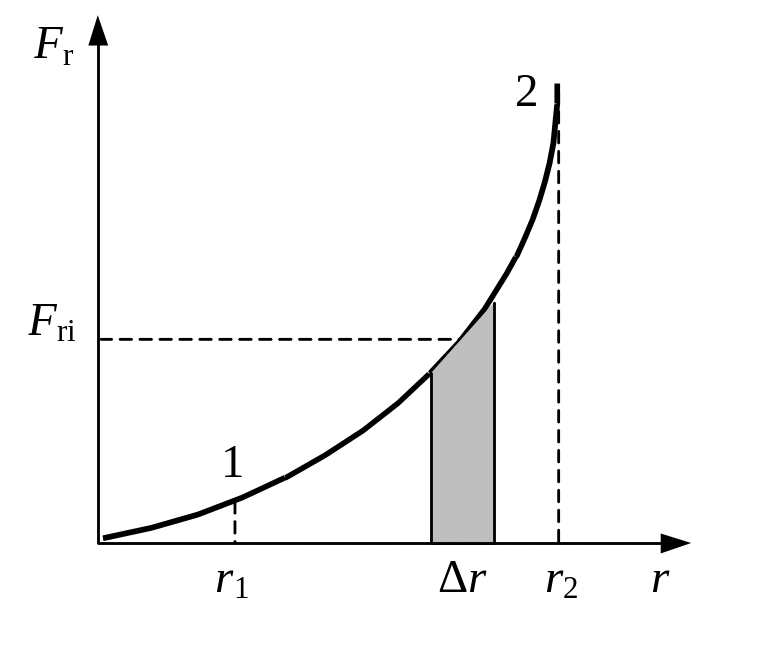Рис. 2.16

акон сохранения энергии. Единой мерой различных форм движения с точки зрения их количественной характеристики является скалярная величина Е, называемая энергией. Энергия не исчезает и не возникает, а переходит из одного вида в другой. Работа – скалярная величина А, являющаяся мерой изменения энергии. Работа внешних сил равна изменению энергии А = Е₂ – Е₁. Работа – способ передачи энергии от одного тела другому в виде силового взаимодействия тел, при котором может изменяться любой вид энергии. Работа силы на малом участке пути определяется как скалярное произведение силы и перемещения: dΑ = ( ,d ), а работа на всем пути равна:

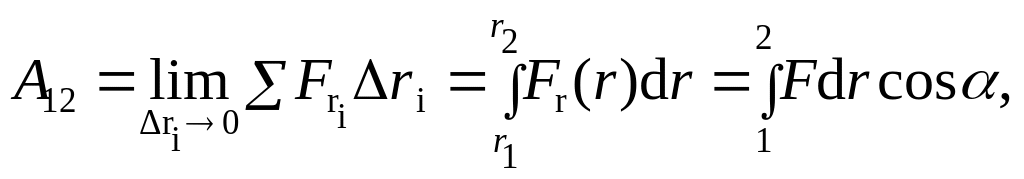где F_r – проекция силы на направление движения точки ее приложения, а α – угол между силой и этим направлением (рис.2.16). Работа и энергия измеряются в джоулях (Дж = Н·м).

Мощность. Средняя мощность – отношение работы к интервалу времени. Мгновенная механическая мощность равна

N = = = ( , ) = F_rv.

Мощность измеряется в ваттах (Вт = Дж/с).

Кинетической энергией (Е_к) называется энергия, связанная с движением тела и зависящая от его скорости. Скорость тела изменяется под действием результирующей силы , работа которой равна

A = F_r dr = m a_r vdt = m vdt = m = mv₂² - mv₁².

Видно, что кинетическую энергию можно определить как Е_к = . Полученное тождество, утверждающее, что изменение кинетической энергии равно работе результирующей силы, называют теоремой о кинетической энергии.

Кинетическая энергия системы точек определяется как сумма кинетических энергий всех точек системы и равна:

Е_к = + Е_отн,

где m – масса системы, _ц – скорость ее центра, Е_отн – кинетическая энергия в системе центра масс (теорема Кенига).

Изменение кинетической энергии системы равно работе всех сил, действующих на ее точки.

Консервативные силы. Сила взаимодействия между точками называется консервативной, если работа этой силы зависит только от начального и конечного положения точек, но не зависит от траектории их перемещения (сила упругости, сила тяжести). Силы, не удовлетворяющие этому условию, называют неконсервативными (сила трения, сила сопротивления). Поле консервативных сил взаимодействия, создаваемое неподвижными внешними источниками, является потенциальным полем (поле тяготения, электростатическое поле).

Потенциальная энергия. Потенциальная энергия (E_п) характеризует взаимодействие между материальными точками и зависит от их взаимного расположения. Разность потенциальных энергий для двух положений точки определяют как работу поля по ее переносу из одного положения в другое:

Е_п ( ₁) – E_п ( ₂) = A₁₂ .

Следовательно, изменение потенциальной энергии _п = E_п( ₂) - Е_п( ₁) = - A равно работе сил поля, взятой с обратным знаком с точностью до константы. Однозначное определение значения возможно, если задана величина потенциальной энергии в какой–то точке пространства или задана точка с нулевой потенциальной энергией.

Например, работа силы тяжести m при перемещении точки массой m с высоты h на высоту h равна (m h – m h ). Отсюда следует, что потенциальная энергия точки в поле тяжести равна Е_п = m h, где высота отсчитывается от оговоренного нулевого уровня.

Работа силы упругости равна (-kx)dx = kx₁² - kx₂², где x₁, x₂ - начальная и конечная деформации пружины. Следовательно, потенциальная энергия упругой пружины равна Е_п = kx², где за нуль принята энергия недеформированной пружины.

Работа сил трения, сопротивления отрицательна как на каждом участке пути, так и вдоль замкнутой траектории. Так как сила трения и скорость точки имеют противоположные направления, работа силы трения на каждом участке пути отрицательна:

dA = d = dt = - Fvd t = - Fds < 0.

Силы трения типичные неконсервативные (диссипативные) силы.

Для двух близких точек на одной оси x разность потенциальных энергий определяется соотношением E_п(x) – E_п(x + dx) = F_xdx. Следовательно, проекция силы на произвольное направление выражается через производную от потенциальной энергии F_x = - . Получаем, что вектор силы равен градиенту потенциальной энергии:

= - ( ) = - gradE_п.

Для центрального поля проекция силы равна F_r = - .

Механическая энергия системы Е_мех определяется как сумма ее кинетической энергии Е_к, потенциальной энергии взаимодействия между частицами внутри системы Е_{п внктр} и потенциальной энергии во внешнем поле Е_{п внешн}:

Е_мех = Е_к + Е_{п внутр} + Е_{п внешн} ,

где сумма (Е_к + Е_{п внутр}) определяет собственную механическую энергию системы. Кроме того, кинетическая энергия системы равна Е_к = + Е_отн, то есть энергии ее движения как целого и кинетической энергии взаимодействия частиц Е_отн – внутренней энергии системы.

Изменение кинетической энергии равно работе всех сил (консервативных и неконсервативных), приложенных к точкам системы: ∆Ε_к = A_конс + A_неконс.

Изменение потенциальной энергии равно работе всех консервативных сил (внутренних и внешних, включая работу потенциальных полей), взятой с обратным знаком:

∆Ε_п = - A_конс .

Получается, что изменение механической энергии равно работе всех неконсервативных сил: ∆Ε_мех = ∆Ε_к + ∆Ε_п = A_неконс.

Полная энергия, кроме механической энергии, включает в себя также различные виды внутренней энергии: тепловую, химическую, ядерную. Общий принцип сохранения энергии вытекает из однородности времени, означающего независимость законов движения от выбора начала отсчета времени.

Закон сохранения энергии гласит: полная энергия замкнутой системы сохраняется, и при этом механическая энергия замкнутой консервативной системы остается постоянной.

Закон сохранения момента импульса. Моментом импульса материальной точки относительно центра О называют векторную величину:

= [ , ],

где – радиус-вектор материальной точки, проведенный из центра О, – импульс точки.

Момент импульса это одна из мер механического движения точки или системы. При движении с постоянной скоростью момент импульса не меняется. Модуль момента импульса равен L = prsinα = pd, где α – угол между импульсом и радиусом - вектором, d – расстояние между центром О и линией действия импульса, которое называют плечом импульса.

Моментом импульса точки относительно оси z называется проекция L на эту ось момента импульса относительно любой точки на этой оси. Момент импульса относительно оси определяется проекцией импульса точки на плоскость, перпендикулярную к оси. Если разложить и на параллельную и перпендикулярную составляющие к оси, соответственно,

= + и = + ,

то составляющие параллельные оси, не дадут вклада в проекцию момента импульса на ось. Следовательно, L = [ , ] . Модуль момента относительно оси также равен произведению импульса на плечо.

Производная по времени от момента импульса материальной точки относительно центра О равна:

= [ ] + [ ] = [ , ] + [ , ] = ,

г

Рис. 2.17

де - момент результирующей силы относительно центра О (член [ , ] = 0 в силу параллельности векторов и ).

Момент силы относительно центра О (рис. 2.17) определяется равенством:

= [ , ],

где – радиус-вектор точки приложения силы . Момент силы не меняется при перемещении силы вдоль линии ее действия.

М

Рис. 2.18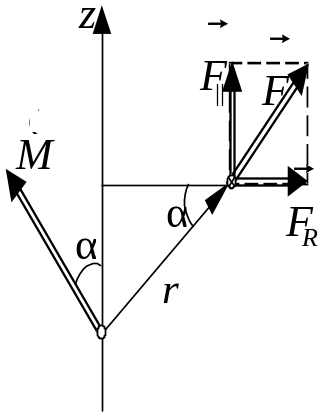

омент силы, векторная величина, характеризующая вращательный эффект силы при действии ее на твердое тело. Модуль момента равен M = Frsinα = Fl, где α – угол между силой и радиусом – вектором, l – расстояние между центром О и линией действия силы, которое называют плечом силы.

Моментом силы относительно оси z (рис. 2.18) называют проекцию М на эту ось момента сил относительно любой точки на этой оси. Аналогично свойствам момента импульса, момент силы относительно оси определяется проекцией силы точки на плоскость, перпендикулярную оси: М = [ ] . Модуль момента относительно оси равен произведению силы на плечо.

Моментом импульса системы материальных точек относительно центра О называется сумма моментов импульса материальных точек, составляющих эту систему. Момент импульса системы равен:

= [ _ц, ] + _отн ,

где _отн – момент импульса в системе центра масс. Суммируя уравнение

= = _внутр + _внешн по всем точкам системы и учитывая, что суммарный момент внутренних сил _внутр равен нулю, получим

= _внешн ,

то есть производная по времени от момента импульса системы равна суммарному моменту внешних сил _внешн.

Закон сохранения момента импульса замкнутой системы выводится из условия, что импульс внешних сил для замкнутой системы равен нулю ( _внешнdt = 0). При этом приращение момента импульса d = 0, а момент импульса замкнутой системы сохраняется =const. Закон сохранения момента импульса является фундаментальным законом, отражающим изотропность пространства, то есть равноправие всех его направлений. Как и в случае законов сохранения импульса и энергии, действие закона сохранения момента импульса выходит за пределы ньютоновской механики, в рамках которой он был выведен.

Момент импульса незамкнутой системы сохраняется в следующих случаях:

1. Если суммарный момент внешних сил _внешн = 0.

2. Если момент импульса внешних сил относительно некоторой оси равен нулю, то момент импульса относительно этой оси сохраняется.

Столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию, называется абсолютно упругим ударом. В этом случае выполняются законы сохранения импульса и механической энергии.