3.4. Вынужденные механические колебания. Резонанс

Колебательное движение системы под воздействием внешней периодической силы называют вынужденными колебаниями, а саму внешнюю силу F (t) называют вынуждающей силой. Из уравнения движения

т = -kx - b + F_x(t)

получим уравнение вынужденных колебаний

+ 2 + ω₀²x = f(t),

где принято обозначение f(t) = .

Общее решение такого неоднородного (с правой частью не равной нулю) дифференциального уравнения может быть представлено в виде суммы частного (то есть любого) решения неоднородного дифференциального уравнения и общего решения однородного (с правой частью равной нулю) дифференциального уравнения, то есть уравнения затухающих колебаний, для которого f(t) = 0.

Частным решением данного неоднородного уравнения могут быть установившиеся колебания. Так как любая периодическая сила F_x(t) может быть разложена в ряд Фурье, то естественно исследовать установившиеся вынужденные колебания под действием гармонической вынуждающей силы f(t) = = cost. Установившиеся колебания имеют вид гармонических колебаний такой же частоты, но со сдвигом по фазе: x(t) = Acos(t + φ).

После математических преобразований находим

А

Рис. 3.7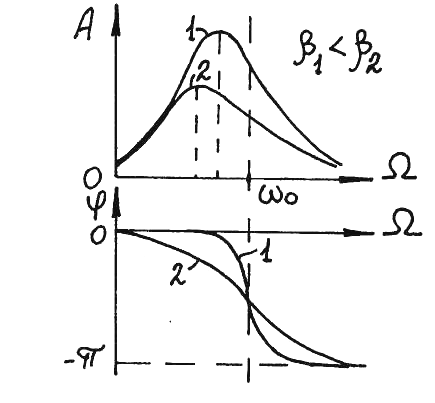

= , tgφ = - .

При  = 0 получается, что φ = 0 и А = = , что соответствует статическому смещению тела вслед за медленно меняющейся силой. При    имеем А  0 и φ  -. Графики зависимости А() и φ() приведены на рис. 3.7.

Резонанс. Максимальное значение амплитуды установившихся колебаний достигается при резонансной частоте :

_рез = =

и равно

А_мах = А(_рез) = ,

г

Рис. 3.8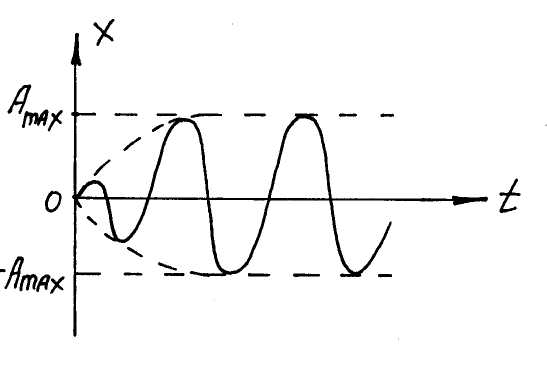

де ω = - циклическая частота затухающих колебаний. При   ω₀ зависимость А() содержит резкий и узкий максимум при резонансной частоте, которая в этом пределе близка к собственной частоте колебаний системы. Это явление называется резонансом, а кривые зависимости А() – резонансными кривыми. Характеристики максимумов (при   ω₀): отношение А_мах к статическому отклонению А(0) равно = ( - логарифмический декремент затухания); величина Q = - добротность колебательной системы. Ширина максимума на уровне равна коэффициенту затухания: ∆  .

Амплитуда установившихся колебаний скорости достигает максимального значения при  = ω₀. При резонансе колебания скорости происходят в фазе с колебаниями возмущающей силы.

Рассмотрим процесс установления колебаний при частоте вынуждающей силы, равной резонансной частоте (при ω₀). Если в начальный момент смещение и скорость точки равнялись нулю, то в рассматриваемом пределе начальным условиям удовлетворяет решение:

х  А_мaxsinωt + А_мaxexp(-t)sinωt = А_мax[1 - exp(-t)]sinωt.

Полученная зависимость изображена на рис. 3.8. При t  амплитуда растет пропорционально времени: A(t)  А_мaxt = ; затухание на этом этапе влияния не оказывает. Время установления колебаний велико по сравнению с периодом:  . Если частота  близка к , но отличается от нее, то движение на начальном этапе t  представляет собой сумму колебаний с близкими частотами. Если выполнено условие   |  -  |  , то в процессе установления колебаний происходят явно выраженные биения (то есть амплитуда колебаний возрастает почти до 2А_мax и уменьшается почти до нуля с периодом Т_б = .