Пример решения задачи

Найдите отклоняющее действие силы Кориолиса на тело, свободно падающее с высоты h на экваторе Земли.

Решение: Так как отклонение падающего тела от вертикали будет незначительное, то в первом приближении можно подставлять в силу Кориолиса _кор = 2m скорость невозмущенного падения = t. Так как вектор перпендикулярен , то сила Кориолиса направлена в сторону востока, равна 2mv и сообщает телу горизонтальное ускорение а_вост= 2gt. Интегрируя, находим горизонтальную скорость v_вост = gt² и горизонтальное перемещение s_вост . Подставив сюда время падения t = , найдем конечное отклонение. Например, для h = 300 м отклонение составляет s 10 см.

2.9. Специальная теория относительности

Теория абсолютного пространства и времени просуществовала всего два столетия. На рубеже 19 – 20 веков квантовая механика Шредингера и теория относительности Эйнштейна позволили осознать, что окружающий мир не трехмерен, а четырехмерен, и в нем время, взаимосвязанное с пространством, играет особую роль. Все вокруг стало относительным и вероятностным, многие точные понятия начали терять смысл, и время стало зависеть от скорости и степени искривленности пространства.

Мир Галилея и Ньютона был Евклидов – бесконечен и однороден, - хотя уже время рассматривалось как важная и особая координата. Происходящие процессы описывались в непрерывном и бесконечном пространстве-времени. Ньютоновская механика опиралась на абсолютное и единое время.

В 1905 году А. Эйнштейн предложил теорию относительности, суть которой заключалась в том, что на быстро движущемся объекте время течет медленнее, изменяются параметры тел и их свойства. То есть время стало величиной относительной.

В 1908 году немецкий ученый Г. Минковский доказал неразрывное единство пространства и времени и ввел новое понятие пространство-время. Мир стал четырехмерным.

В 1916 году Эйнштейн завершил создание специальной теории относительности (СТО), согласно которой пространство-время может искривляться под действием сил тяготения (математически искривленные пространства описал Н. Лобачевский в неевклидовой геометрии). Было открыто, что в сильном поле тяготения время течет медленнее. Эти эффекты были названы релятивистскими (relative – относительный).

Постулаты СТО. Специальная теория относительности Эйнштейна расширяет границы классической ньютоновской физики, действующей в области нерелятивистских скоростей, малых по сравнению со скоростью света с, на любые, в том числе релятивистские, то есть сравнимые с с, скорости. Все результаты релятивистской теории при → 0 переходят в результаты классической нерелятивистской физики (принцип соответствия).

Специальная теория относительности опирается на два постулата:

Первый постулат: все физические законы – как механические, так и электромагнитные – имеют одинаковый вид во всех инерциальных системах отсчета (ИСО).

Второй постулат Эйнштейна: скорость света в вакууме одинакова для всех инерциальных систем отсчета и равна c ≈ 3·10⁸ м ⁄ с. Этот постулат содержит сразу два утверждения:

а) скорость света с не зависит от скорости v источника,

б) скорость света c не зависит от того, в какой инерциальной системе отсчета находится приемник, то есть не зависит от скорости приемника v.

П

Рис. 2.39

реобразования Лоренца. Принцип относительности Галилея утверждает, что все законы механики имеют одинаковый вид во всех ИСО. Пусть система К' движется относительно системы К с постоянной скоростью (рис. 2.39).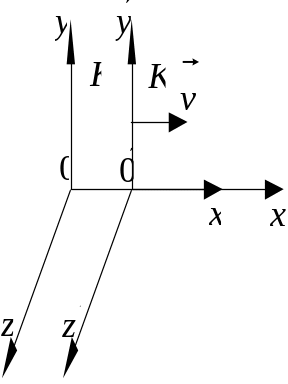

Тогда координаты и время события в системе К' будут выражаться через координаты и время в К с помощью преобразований Галилея (для случая систем координат с параллельными осями, с осями x' и x, направленными вдоль и отсчетом времени от момента полного совмещения осей):

x' = x – vt, y' = y, z' = z, t' = t.

Преобразования Галилея основаны на утверждениях о независимости хода времени и длины отрезков от системы отсчета, которые считались неотъемлемыми свойствами пространства и времени. Уравнение движения инвариантно (имеет одинаковый вид в разных системах отсчета) относительно преобразований Галилея. Теория относительности показывает, что преобразования Галилея верны только при v << c и их заменяют преобразования Лоренца, верные при любых скоростях v < c.

При таком же выборе осей координат и отсчета времени, как в преобразованиях Галилея, преобразования Лоренца имеют вид:

x' = γ (x – vt), y' = y, z' = z, t' = γ(t – x),

где величина γ определяется из равенства γ² = 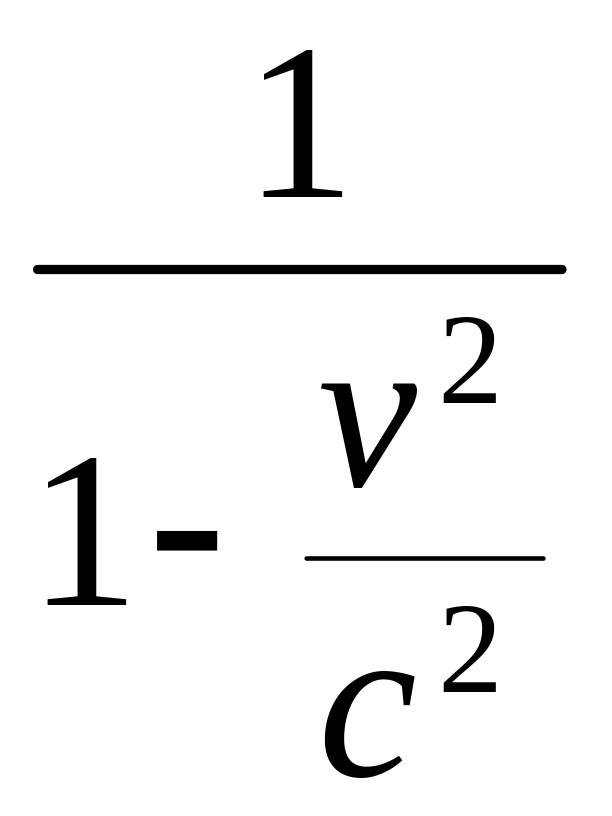, γ ≥ 1.

Преобразования Лоренца для разности координат и времен двух событий имеют вид:

∆x' = γ(∆x – v∆t), ∆y' = ∆y, ∆z' = ∆z, ∆t' = γ(∆t – ∆x).

Обратные преобразования из К' в К получаются при замене v на ( – v):

∆ x = γ(∆x' + v ∆t'), ∆y = ∆y', ∆z = ∆z', ∆t = γ(∆t' + ∆x').

Длина тела в разных системах. Длина движущегося тела определяется как расстояние между точками, где концы отрезка, длина которого равна продольному размеру тела, находились одновременно (то есть ∆t = 0). Предположим, что с телом, движущимся поступательно в системе К в направлении оси х со скоростью , связана система координат К' (рис. 2.40).

Собственный продольный размер тела L₀, измеренный в системе К', в которой тело неподвижно, равен

L₀ = x₂' – x₁'.

В системе К продольные размеры тела определяются аналогичным образом и равны

L = x₂ – x₁.

Из преобразований Лоренца, в которых надо учесть, что это одновременно скорость тела и системы К' относительно К и, что для мгновенного определения длины t₁ = t₂ (то есть ∆t = 0), получим

L₀ = x₂' – x₁' = γ(x₂ – vt₂) - γ(x₁ – vt₁) = γ(x₂ – x₁ - vt₂ + vt₁) = γ(x₂ – x₁) = γL.

То есть, продольные размеры тела, движущегося со скоростью v → c, сокращаются:

L = .

Поперечные размеры движущегося тела не изменяются.

Относительность хода времени. Из преобразований Лоренца видно, что время протекает по-разному в разных ИСО. В частности, события, происходящие в системе К одновременно (∆t = 0), но в разных точках пространства, в К' могут быть не одновременными: ∆t' = - может быть как положительным, так и отрицательным (относительность одновременности). Часы, движущиеся вместе с системой отсчета (то есть неподвижные относительно К', или ∆x' = 0), показывают собственное время этой ИСО. С точки зрения наблюдателя в системе К, эти часы отстают от его собственных (замедление хода времени). Рассматривая два отсчета движущихся часов как два события, получим:

∆t = γ(∆t' + ∆x') = γ∆t'.

Равноправие всех ИСО проявляется в том, что с точки зрения наблюдателя К' часы, неподвижные относительно К, будут отставать от его собственных.

Сложение скоростей в СТО. Если частица движется со скоростью относительно ИСО К', то ее скорость относительно К можно найти, выразив dx, dy, dz, dt из формул:

∆x = γ(∆x' + v∆t'), ∆y = ∆y', ∆z = ∆z', ∆t = γ(∆t' + ∆x'),

подставив в формулы для скоростей v_x = , v_y = , v_z = . Откуда получаются следующие соотношения:

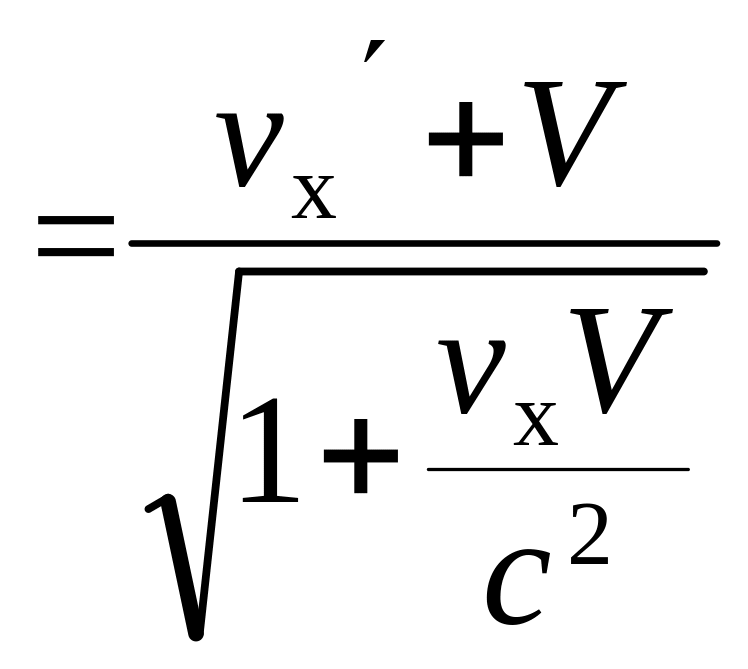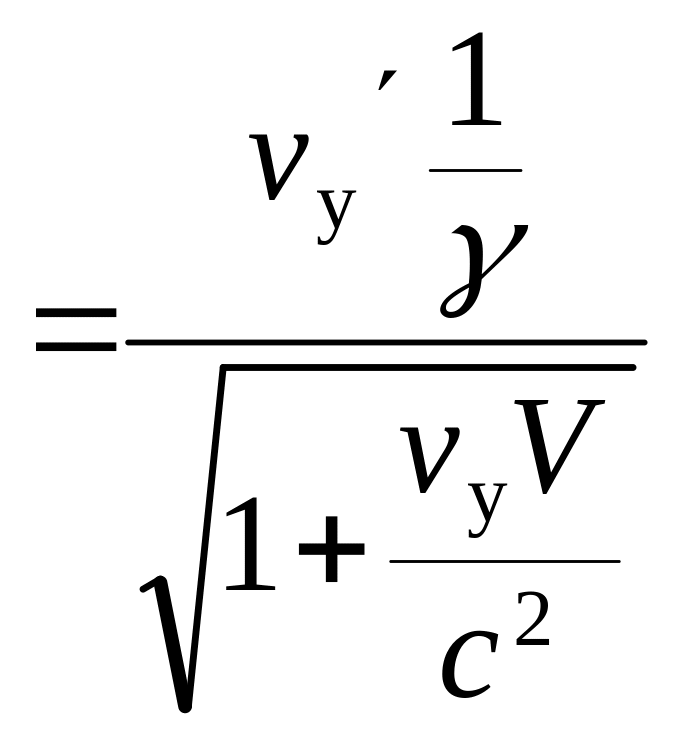v_x , v_y , v_z .

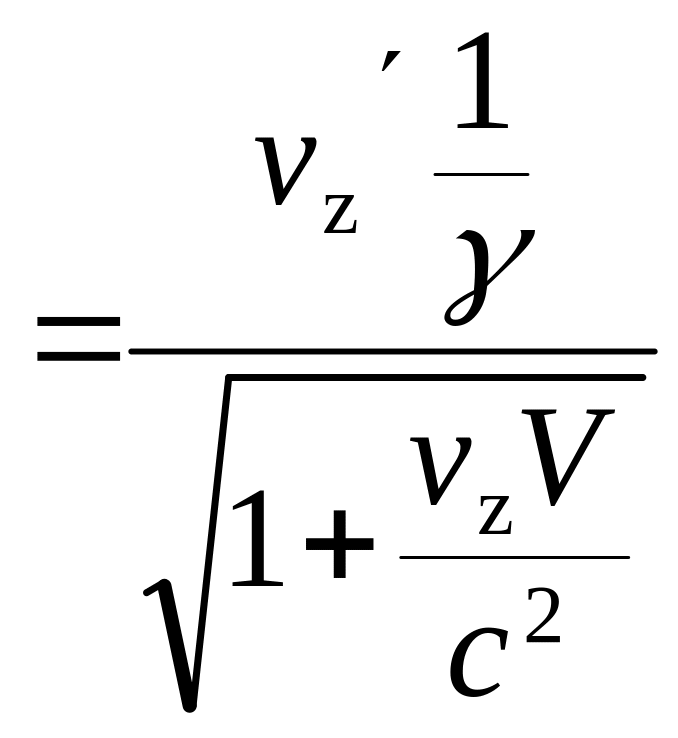При v_x << c и V << c происходит переход к нерелятивистскому закону сложения скоростей. Если V и v меньше c, то и скорость тела v относительно К будет меньше c. Скорость света c является максимально возможной скоростью передачи взаимодействий в природе.

Интервал. Преобразования Лоренца не сохраняют ни величину интервала времени, ни длину пространственного отрезка. В обычном пространстве расстояние ∆L между двумя точками определяется выражением (∆L)² = (∆x)² + (∆y)² + (∆z)² и является инвариантом, то есть не зависит от выбора системы координат. В четырехмерном пространстве-времени аналогичное выражение для расстояния между двумя точками (c∆t)²+(∆x)²+(∆y)²+(∆z)² при переходе к другой ИСО изменяет свое числовое значение, однако, при преобразованиях Лоренца сохраняется величина

s₁₂² = (c∆t)² - (∆x)² - (∆y)² - (∆z)² = (c∆t)² - (∆r)²,

где s₁₂ называется интервалом между событиями 1 и 2 (∆t = t₂ – t₁, ∆r = r₂ – r₁). Если s₁₂² > 0, то интервал между событиями называют временеподобным, так как в этом случае существует ИСО, в которой ∆ r = 0, то есть события происходят в одном месте, но в разное время. Если s₁₂² < 0, то интервал между событиями называют пространственноподобным, так как в этом случае существует ИСО, в которой ∆t = 0, то есть события происходят одновременно в разных точках пространства. Убедимся в инвариантности интервала. В системе К имеем s = (c∆t)² - (∆x)² - (∆y)² - (∆z)². В системе К' для тех же событий (s₁₂')² = (c∆t')² - (∆x')² - -(∆y')²- (∆z')². Подстановка ∆x' = γ(∆x –V∆t), ∆y' = ∆y, ∆z' = ∆z, ∆t' = γ(∆t – ∆x) в выражение для (s₁₂')² приводит к равенству (s₁₂')² = s₁₂², что доказывает инвариантность интервала.

Лоренцевы четырехмерные векторы (4-векторы). Величина (A_x, A_y, A_z, A_) = ( , A_), которая при переходе из системы К в систему К' преобразуется так же, как (x, y, z, ct), то есть:

A_x' = γ (A_x – A_), A_y ' = A_y, A_z' = A_z, A_' = γ(A_ – A_x),

называется лоренцевым четырехмерным вектором. Величины A_x, A_y, A_z– пространственные компоненты 4-вектора, а A_ - его временная компонента. Сумма двух 4-векторов и произведение 4-вектора на число – тоже 4-вектор. При изменении ИСО сохраняется величина, аналогичная интервалу:

A² = A_² - ( )²,

а также скалярное произведение (A_B_ - ). Физическое равенство, записанное в виде равенства двух 4-векторов, остается верным во всех ИСО.

Импульс и энергия в СТО. Релятивистский 4-вектор импульса определяют как

= m = γm , p_ = md = γmc,

где d = γdt – бесконечно малое изменение собственного времени частицы (измеренное в ИСО), скорость которой равна скорости частицы в данный момент. Пространственные компоненты 4-вектора образуют релятивистский импульс = γm , а временная компонента p_ = , где Е – релятивистская энергия частицы: Е = γmc², поэтому 4-вектор ( ) называют 4-вектором энергии-импульса. Релятивистские энергия и импульс связаны соотношением: = . При переходе в другую ИСО энергия и импульс преобразуются по закону: p_x' = γ(p_x – ), p_y' = p_y, p_z' = p_z, E' = γ(E –Vp_x). Релятивистская энергия частицы не равна нулю при v = 0, то есть она состоит из энергии покоя mc² и кинетической энергии:

Е = γmc² = mc² + Е_к,

причем релятивистская кинетическая энергия при << 1 переходит в классическую кинетическую энергию. Так как величина - p² сохраняется, ее можно вычислить в системе отсчета, где частица в данный момент покоится:

- p² = m²c² или E² – p²c² = m²c⁴.

Для частиц с массой, равной нулю (фотонов), связь между энергией и импульсом принимает вид:

Е = рc.

Между импульсом и кинетической энергией возможно соотношение:

p²c² = Е_к(Е_к + 2mc²).

Законы сохранения, как и другие законы природы, должны соблюдаться во всех ИСО, то есть быть инвариантными по отношению к преобразованиям Лоренца. Запишем законы сохранения релятивистской энергии и релятивистского импульса для абсолютно неупругого удара двух тел массой m каждое, двигавшихся навстречу друг другу с одинаковой скоростью v.

Закон сохранения энергии будет иметь вид 2γmc² = Мc², а закон сохранения импульса записывается как 2γ²mv = γМv, где масса составной частицы после соударения М равна 2γm. Видно, что масса М больше суммы начальных масс частиц. Увеличение внутренней энергии при неупругом ударе на ∆Е приводит к увеличению массы составной частицы на .