5.Дифференциальные уравнения и основные задачи динамики материальной точки
5.1.Основные положения динамики. Аксиомы динамики
В динамике механическое движение рассматривается не только с точки зрения геометрических форм движения, но и выясняются факторы, вызывающие те или иные виды движений. Динамика изучает движение материальных тел под действием сил.
В основе динамики лежат следующие аксиомы.
Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Принцип инерции лежит в основе статики и динамики потому, что содержит в себе как аксиому инерции покоя (статика), так и аксиому инерции движения (динамика). Таким образом, если на материальное тело (точку) не действуют никакие силы или действует уравновешенная система сил (Fk=0, Mo(F)=0), то относительно неподвижной (инерциальной ) системы отсчета скорость тела (точки) v=const. Но при v=0 имеем состояние покоя, а при v0 (точка движется равномерно и прямолинейно) – состояние динамического равновесия.
Из первой аксиомы следует, что вывести материальную точку из состояния инерции может только приложенная сила, но из кинематики известно, что начало движения материальной точки из состояния покоя либо нарушение ее прямолинейного или равномерного движения связано с возникновением ускорения. Зависимость между внешней силой, действующей на материальную точку, и возникшим вследствие этого ускорением устанавливает аксиома 2.
Аксиома 2 (основной закон динамики). Ускорение материальной точки пропорционально действующей силе и направлено по линии, вдоль которой действует эта сила
F=ma.
На все материальные тела вблизи Земли действует сила тяжести G и при свободном падении на Землю тела любой массы m приобретают одно и тоже ускорение g, которое называется ускорением свободного падения. Для свободно падающего тела можно записать:
G=mg.
Значение силы тяжести тела в ньютонах равно произведению его массы на ускорение свободного падения.
Аксиома 3 (закон независимости действия сил). Если к материальной точке приложена система сил, то движение этой точки складывается из тех движений, которые точка могла бы иметь под действием каждой силы в отдельности.
Таким образом, при одновременном действии на материальную точку массой m, например, четырех сил (рис. 5.1) ускорение a , полученное точкой, можно определить, геометрически сложив ускорения a1, a2, a3, a4, возникшие под действием каждой силы в отдельности. В то же время ускорение a пропорционально равнодействующей F тех же сил:
F=ma,
где F=Fk и a=ak .
Аксиома 4 (закон действия и противодействия). Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны.
Силы взаимодействия между двумя материальными точками не уравновешивают друг друга, так как одна сила приложена к одной точке, а вторая к другой. Согласно аксиоме 2, каждая из этих сил сообщает ускорение той материальной точке, на которую действует. Таким образом, все ускорения материальных точек относительно неподвижной (инерциальной) системы отсчета есть результат взаимодействия материальных точек, а в общем случае – результат взаимодействия материальных тел.
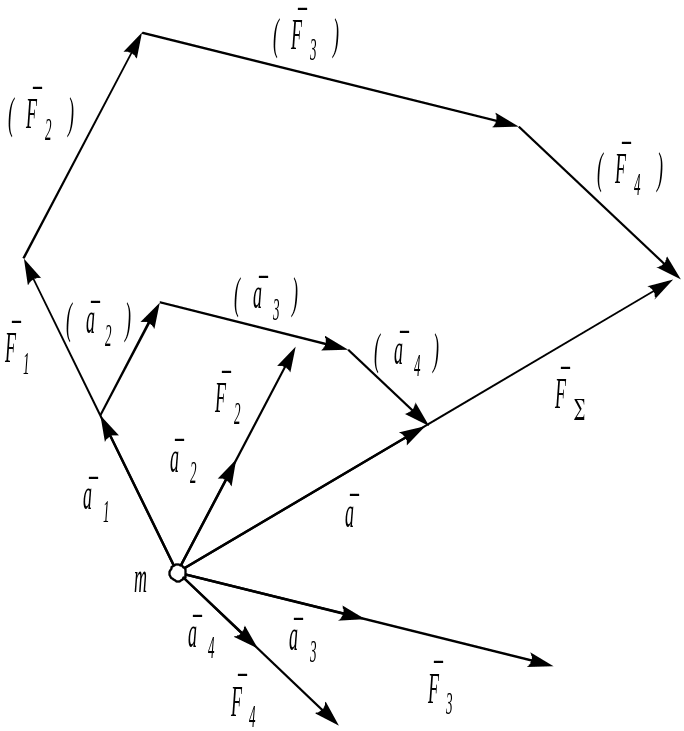
Рис. 5.27
Материальная точка, движение которой в пространстве не ограничено наложенными связями, называется свободной.
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.