23.1.Кинетическая энергия механизма

Кинетическая энергия звена механизма зависит от массы звена, ее распределения, скорости центра масс и угловой скорости звена.

Кинетическая энергия механизма, состоящего из k звеньев, определяется по формуле:

где m_i – масса i-го звена; J_ci – момент инерции i- го звена относительно оси, проходящей через центр масс; v_ci – линейная скорость центра масс i-го звена; _i – го звена.

Изменение кинетической энергии механизма равно сумме работ активных сил, действующих на звенья механизма:

T – T₀=A_д – A_с,

где T – кинетическая энергия механизма в его конечном положении;

T₀ – кинетическая энергия механизма в его начальном положении;

A_д – работа движущих сил;

A_с – работа сил сопротивления

23.2.Приведение масс и сил

Решение задач динамики значительно упрощается, если действительные массы звеньев механизма с одной степенью подвижности заменить эквивалентной им одной приведенной массой, перенесенной условно на какое-либо звено, которое принято называть звеном приведения.

Приведенная масса должна иметь кинетическую энергию, равную кинетической энергии механизма. В качестве звена приведения чаще всего выбирают начальное звено.

Кинетическая энергия приведенной массы, сосредоточенной в данной точке звена приведения:

где m_п – приведенная масса; v – скорость точки приведения.

Из выражений для кинетической энергии механизма и звена приведения можно получить формулу для определения приведенной массы:

.

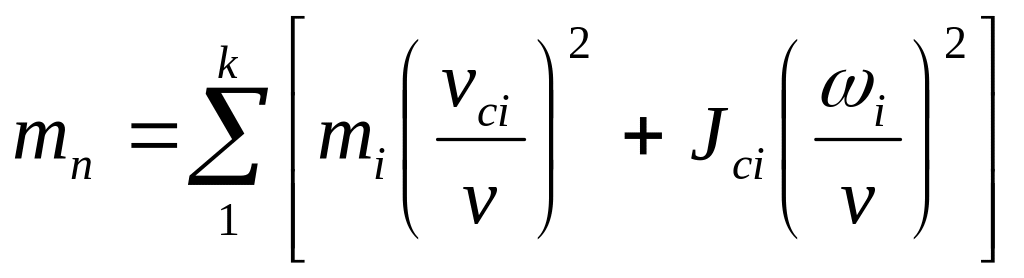Если звеном приведения является звено, совершающее вращательное движение, то вычисляют приведенный момент инерции:

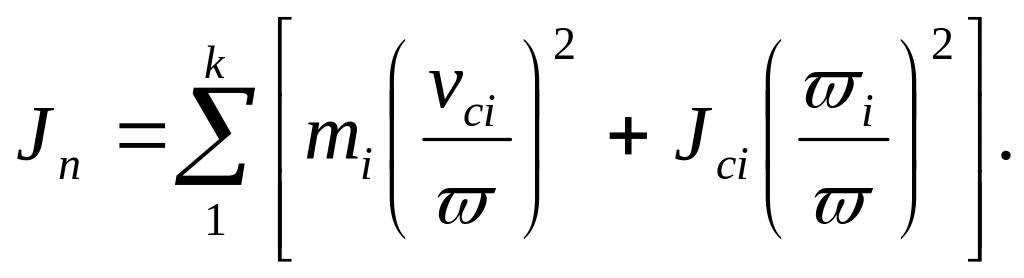
Кинетическая энергия звена приведения в этом случае определяется по формуле:

Силы и моменты, действующие на звенья механизма, можно условно заменить приведенной силой или приведенным моментом, приложенным к звену приведения. При этом приведенная сила или приведенный момент должны производить работу, равную работе всех активных сил, действующих на звенья механизма, на соответствующих перемещениях. Мощность, развиваемая приведенной силой или приведенным моментом, также должна быть равна мощности всех активных сил, приложенных к звеньям механизма.

Мощность, развиваемая приведенной силой,

N=P_пv,

где P_п – величина приведенной силы; v – скорость точки приложения приведенной силы.

Мощность, развиваемая приведенным моментом,

N=M_п,

где M_п – приведенный момент;  – угловая скорость звена приведения.

Мощность всех активных сил, действующих на звенья механизма,

где P_i и M_i – сила и момент, приложенные к звену i;

v_i – скорость точки приложения силы P_i;

_i – угловая скорость звена i ;

_i – угол между силой P_i и скоростью v_i.

Приравняв мощности активных сил и приведенной силы, получим выражение для определения величины приведенной силы:

.

Аналогично можно определить величину приведенного момента:

.

23.3.Режимы работы машин

В работе машин возможны два режима: установившегося и неустановившегося движения.

Режим установившегося движения характеризуется периодическим изменением скорости, ускорения, силы и других механических величин, зависящих от времени. Если эти величины изменяются не периодически, то режим работы машин называется неустановившимся. Режим неустановившегося движения характерен для фазы разбега и фазы выбега машин (рис. 21.1).

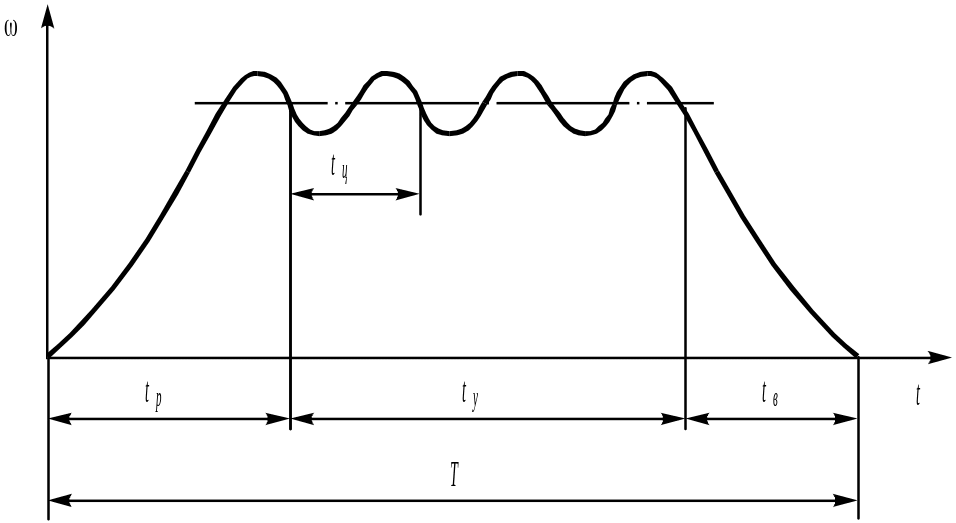
Рис. 23.125

При разбеге машины угловая скорость начального звена в конце каждого периода больше угловой скорости, соответствующей началу периода. При выбеге угловая скорость начального звена в конце периода меньше угловой скорости в начале периода. Изменение угловой скорости  за период при установившемся движении машины =0, при разбеге >0, при выбеге <0.

Поэтому изменение кинетической энергии машины за период при разбеге будет T – T₀>0, при установившемся движении T – T₀=0, при выбеге

T – T₀<0.

Таким образом, при разбеге происходит приращение кинетической энергии. Работа движущих сил в стадии разбега расходуется на преодоление сопротивлений и на повышение кинетической энергии машины. При установившемся движении работа движущих сил полностью расходуется на преодоление производственных и непроизводственных сопротивлений. Во время выбега происходит отдача кинетической энергии, накопленной во время разбега.