Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

гидромеханика нефти

.pdf

Скачиваний:

Добавлен:

02.01.2021

Размер:

20.67 Mб

Скачать

☆

1 / 461 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

СПБГУАП| Институт 4 группа 4736

ЗАКОНЫ СОХРАНЕНИЯ							45
В качестве поверхности S возьмем замкнутую поверхность, состоя-
щую из живых сечений трубки тока S1 ,					S2 и ее боковой поверхности S3

(рис.2.4). В живом сечении S1 v = −				nv ,	в S2 v =	nv , на боковой поверх-
			– единичный вектор,
ности S3 v =	τ1v , где	τ1	– единичный вектор,			лежащий в касательной
плоскости к трубке тока. Тогда с учетом соотношения (1.26) получим
			pnnvdS+	∫ pnnvdS+
∫	pnvdS = − ∫		pnnvdS+	∫ pnnvdS+		∫ pnτ vdS .	(2.68)
S		S1		S2		S3

Подставив выражения (2.67) и (2.68) в уравнение (2.66) и повторяя рас-

суждения, приведенные при выводе соотношений (2.26) и (2.27), получим

∂	ρ		v2	− Π
∫	ρ	u +		− Π
V ∂ t			2
V ∂ t			2

= ∫ (Π ρ + pnn)v dS −

∂ ρ

∫ ρ

u +

v dS −

u +

v dS =

∂ t

(2.69)

∫( Π ρ + pnn) v dS + ∫ pnτ 1v dS +

∫ ρ qe dV.

Соотношение (2.69) представляет собой выражение закона сохранения энергии для трубки тока при наличии потенциала напряжения массовых сил. При установившемся движении оно принимает вид

∫

v dS −

∫

u +

ρ v dS =

(2.70)

pnn

∫

Π +

ρ v dS −

∫

ρ v dS

∫

pnτ 1v dS

∫

ρ qe dV.

Воспользовавшись теоремой о среднем значении в интегральном ис-

числении, имеем

ρ v dS=

v2 Ò

∫ρ

v2 Ò

∫ u +

v dS=

Qm ,

pnn

pnn cp

∫

Π +

ρ v dS=

Π +

∫ρ

v=dSΠ +

Qm ,

а так как при установившемся движении вдоль трубки тока Qm = const , то уравнение (2.70) можно представить в виде

−

(2.71)

pnn cp

Π +

−

Π +

∫

pnτ

1v dS +

∫

ρ qe dV,

Qm S3

Qm V

где индексы «1», «2» означают номера соответствующих сечений.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

46 ГЛАВА II

§7. Теорема об изменении кинетической энергии

Для получения математического выражения теоремы об изменении ки-

нетической энергии положим в соотношении (2.23) ϕ =

. Тогда с учетом

уравнения неразрывности (2.25) получим

∫ ρ

∫

div v

dt V

V dt

(2.72)

d v2

= ∫ ρ

= ∫

div v

dV.

V dt 2

2 dt

V dt 2

Подставив в уравнение (2.14) соотношения (2.63) и (2.72), получим

d v

∂

( piv)

(i)

∫ ρ

−

ρ Fv −

−

ρ N

dV =

0 ,

(2.73)

∂

dt 2

а так как это соотношение справедливо для произвольного объема, то

d v

= ρ Fv

∂ ( pi v) +

ρ N(i) .

(2.74)

dt 2

∂ xi

Из уравнения (2.74), то есть из теоремы живых сил для сплошной сре-

ды, следует, что скорость изменения кинетической энергии равна мощно-

сти всех внешних и внутренних сил. При этом в уравнение (2.74) так же,

как и в уравнение (2.75), входят удельные по объему величины.

Для того, чтобы получить теорему живых сил для трубки тока, положим

в соотношении (2.20) ϕ

= ρ

и, воспользовавшись уравнением (2.14), по-

лучим соотношение

∂

ρ v

(i)

vndS =

∫ ρ Fv dV +

∫ pnv dS +

∫ ρ N

dV , (2.75)

∫

dV +

V ∂

представляющее собой интегральную форму теоремы об изменении кине-

тической энергии.

Выберем в качестве замкнутой поверхности S поверхность, ограни-

ченную живыми сечениями трубки тока S1 , S2 и ее боковой поверхно- стью S3 (рис. 2.3), и примем, что напряжение массовых сил обладает по-

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ЗАКОНЫ СОХРАНЕНИЯ	47

тенциалом, то есть что F = Π	. Используя соотношения (2.67) и (2.68),

после рассуждений, аналогичных проведенным при выводе (2.69), из ра-

венства (2.75) получим соотношение

∂

ρ v2

∂ ρ

∫

− Π

dV+

∫

ρ v dS−

∫

ρ v dS=

∂

∂ t

(2.76)

∫

Π +

ρ v dS−

Π∫+

+v dS ∫

pτn

+v dS

ρ∫

) dV,

представляющее собой выражение теоремы об изменении кинетической энергии для трубки тока при наличии потенциала для напряжения массовых сил.

При установившемся движении соотношение (2.76) принимает вид

pnn

∫

− Π

−

ρ v dS −

∫

− Π

−

ρ v dS =

(2.77)

∫

pnτ 1v dS +

∫ ρ N(i) dV

Qm S

Qm V

или

pnn

v2 cp

pnn

v2 cp

− Π −

−

2 2

2 1

(2.78)

∫

pnτ 1vdS +

∫ ρ N(i) dV

Qm S

Qm V

где осреднение по сечениям S1 и S2 имеет тот же смысл, что и в (2.71).

Для вычисления удельной мощности внутренних сил N(i) вернемся к рассмотрению соотношения (2.68).

Умножив уравнения движения в напряжениях (2.42) скалярно на век-

тор скорости v , получим

∂ pi

ρ v

= ρ

ρ Fv +

(2.79)

∂ xi

dt 2

Вычитая почленно соотношение (2.79) из соотношения (2.78), име-

ем

∂ pi v

+ ρ N(i) −

∂ pi

∂ v

+ ρ N(i) = 0

∂ xi

Контакты | https://new.guap.ru/i03/contacts

ле скоростей, в котором

§8.

СПБГУАП| Институт 4 группа 4736

или, так как

ej pij, v

ekvk

ρ N(i) = −

= −

ej pij

= − pik

∂ vk .

∂ v

∂ ekvk

∂ xi

ГЛАВА II

(2.80)

Из равенства (2.80) следует, что если все точки рассматриваемого объе-

ма сплошной среды движутся с одинаковыми скоростями, то есть ес-

ли vk = vk (xj, t) = vk (t) , то N(i) =0. Следовательно, работа внутренних сил может быть отличной от нуля только в пространственно неоднородном по-

∂ vk ≠ 0 . ∂ xi

Уравнение притока тепла

Для получения уравнения, описывающего изменение внутренней энергии, рассмотрим закон сохранения полной энергии (2.65) и вычтем из этого уравнения почленно уравнение (2.74). Тогда получим

	du	= qe − N(i) .	(2.81)

	dt
Соотношение (2.81) содержит удельные (по массе) внутреннюю энер-
гию u , тепловую мощность qe , мощность внутренних сил N(i)			и называ-

ется уравнением притока тепла. Из этого уравнения видно, что при адиа-

батическом процессе, то есть при			qe = 0,		изменение внутренней энергии
может происходить только за счет работы внутренних сил.
С помощью соотношения (2.80) уравнению притока тепла можно при-
дать вид
	du	= qe	+	pik	∂ vi	.	(2.82)
				ρ
	dt				∂ xk

Из уравнения (2.82) следует, что в однородном поле скоростей, т.е. при vi = vi (t) , изменение внутренней энергии определяется только внешним подводом тепла.

Заметим, что уравнение притока тепла, как и теорема об изменении кинетической энергии, не является независимым уравнением – оно есть следствие основных законов сохранения.

Примеры использования уравнения притока тепла приведены в гл. IV.

§9. Система уравнений движения сплошной среды

Из всего вышеизложенного следует, что движения сплошной среды,

определяемые фундаментальными физическими законами сохранения мас-

сы, изменения количества движения, сохранения энергии, описываются

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ЗАКОНЫ СОХРАНЕНИЯ

системой уравнений, состоящей из (2.25), (2.42), (2.65) и имеющей вид

dρ +

div v =

ρ F +

∂

pi ,

(2.83)

∂ xi

= ρ Fv +

∂ ( piv)

+ ρ qe.

u +

∂ xi

Таким образом, система уравнений движения любой сплошной среды состоит из одного векторного и двух скалярных уравнений или пяти ска-

лярных уравнений. В общем случае система уравнений (2.83) содержит 11

скалярных неизвестных*: vi, pij ,ρ , u . Следовательно, она является незамк-

нутой. Это обстоятельство отражает тот факт, что в законах сохранения не содержится никаких параметров, характеризующих свойства конкретных сплошных сред. Поэтому к полученным уравнениям необходимо добавить соответствующие соотношения (связи), задающие физические свойства той или иной сплошной среды. Очевидно, что для разных сплошных сред (таких,

например, как жидкость, упругое тело, пластическое тело и т.д.) эти связи будут иметь различный вид, и полученные, уже замкнутые системы уравне-

ний для разных сплошных сред также будут иметь различный вид.

Установление необходимых для конкретных сред связей требует предва-

рительного изучения деформаций или скоростей деформаций сплошной среды.

Связи между напряжениями и деформациями или между напряжения-

ми и скоростями деформаций называются реологическими уравнениями**.

Таким образом, различным сплошным средам соответствуют различные реологические уравнения.

В заключение заметим, что во всех рассуждениях настоящей главы предполагалось, что в классической механике сплошной среды принят по-

стулат, согласно которому основные законы сохранения считаются спра-

ведливыми не только для всего рассматриваемого тела (в нашем случае – для материального объема), но и для каждой его части, сколь бы мала она ни была. Этот постулат носит название принципа локальности, а диффе-

ренциальные уравнения, являющиеся следствиями интегральных законов сохранения, называют локальными формулировками законов сохранения.

Заметим также, что если система координат, в которой рассматривается движение сплошной среды, подвижна, то все уравнения движения в этой сис-

теме координат сохраняют свой вид, только массовые силы будут включать в себя также и силы инерции, появляющиеся в относительном движении.

* Напряжение массовых сил F и тепловая мощность qe представляют собой внешние воздействия и

считаются заданными.

** Реология (от греческого слова «течение») – наука о деформации материалов.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Глава III

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

§1. Скорость деформации малой частицы. Теорема Гельмгольца

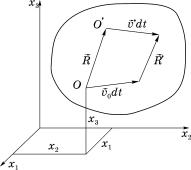
Рассмотрим малую частицу сплош- ной среды, изображенную на рис. 3.1, где точка O – центр частицы с пространст- венными координатами xj, точка O′ – любая точка внутри частицы, век-


тор R(ξ j ) =	OO′ целиком лежит внут-

ри рассматриваемой частицы. Распределение скоростей внутри

частицы в фиксированный момент времени t1 определяется полем скоро- стей, т.е. величинами скоростей точек

O и

O′, соответственно,

v(xi, t1)

+ ξ j , t1 ) , или voi =

vi(xj, t1 ),

Рис. 3.1

и v′ =

v(xj

j +

ξ j

v′

v′(x

, t ). Движение в пределах

частицы предполагается непрерывным и дифференцируемым.

Разлагая vi′ в ряд Тейлора, получаем

i′ = oi + ξ j

∂

+ ... =

i + ... ,

(3.1)

∂

где все производные берутся в точке 0. Так как частица предполагается малой, т.е. ξ предполагаются малыми в сравнении с характерным линей- ным размером в рассматриваемой задаче, то, ограничиваясь в формулах (3.1) членами первого порядка малости, имеем

		∂ vi
vi′ =	voi + ξ j		=	voi +	R vi	(3.2)

		∂ xj

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

или

		+		=		+ Φ R .
v′ =	vo	+	(R )v	=	vo	+ Φ R .

Из равенств (3.2) и (3.3) видно, что разность скоростей v′ − ляется матрицей

	∂ v1	∂ v1	∂ v1

	∂ x1	∂ x2
	∂ x1	∂ x2	∂ x3
Φ =	∂ v2	∂ v2	∂ v2	,

	∂ x1	∂ x2
	∂ x1	∂ x2	∂ x3
	∂ v3	∂ v3	∂ v3
	∂ x1	∂ x2
	∂ x1	∂ x2	∂ x3

(3.3)

vo опреде-

(3.4)

элементы которой представляют собой коэффициенты при членах первого порядка малости в разложении vi′ в ряд Тейлора.

Матрица Φ всегда может быть представлена в виде суммы двух мат- риц, из которых одна симметрична, а другая антисимметрична. Действи- тельно, введем обозначения

ε ik =

∂ vi

∂

∂ v3

−

∂ v2

∂ xk

∂

∂ x2

∂ x3

(3.5)

∂ v1

∂

∂ v2

∂ v1

−

∂ x3

∂

∂ x1

∂ x2

Матрицу (3.4) представим в виде

ε11

ε12

ε13

− ω 3

ω 2

Φ =

ε 21

ε 22

ε 23

ω 3

− ω 1 = D + Ω .

(3.6)

ε 31

ε 32

− ω 2

ω 1

ε 33

Из формул (3.5) видно, что ε ik =

ε ki .

Подставив соотношение (3.6) в формулу (3.3), получаем


				Ro .			(3.7)
		v′ =	vo + DR + Ω	Ro .			(3.7)
Переписывая равенство (3.7) в координатном виде, имеем
v1′ = vo1 + ε11ξ 1 + ε12ξ 2 + ε13ξ 3 − ω 3ξ 2 + ω 2ξ 3,
v′	v	+ ε 21ξ 1	+ ε 22ξ 2 + ε 23ξ	3 + ω 3ξ 1 − ω 1ξ	3	,	(3.8)
2 =	o2	+ ε 21ξ 1	+ ε 22ξ 2 + ε 23ξ	3 + ω 3ξ 1 − ω 1ξ	3

v3′ = vo3 + ε 31ξ 1 + ε 32ξ 2 + ε 33ξ 3 − ω 2ξ 1 + ω 1ξ 2.

Из формул (3.5) следует, что величины ω k представляют собой ком-

поненты вектора ω = ω , который может быть символически записан

ek k

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ГЛАВА III

как


ω = 1		e1	e2	e3	=	1 rot v .
ω = 1		∂	∂	∂	=	1 rot v .


	2	∂ x1	∂ x2	∂ x3		2
		v1	v2	v3

Вектор ω называется вихрем скорости*.

Введем в рассмотрение квадратичную функцию

F = 1 ε ikξ iξ k .

Благодаря тому, что ε ik = ε ki , из формулы (3.10) следует, что

∂ F		= ε ikξ k .
∂ ∂ξ
	i

(3.9)

(3.10)

(3.11)

С помощью формул (3.9) и (3.11) равенства (3.8) можно переписать в виде

vi′ = voi +		∂ F +	(ω × R)i

		∂ ξ i
или
				(3.12)
v′ =	vo +	ω × R + F .		(3.12)

Если бы рассматриваемая малая частица была абсолютно твердой, то, как известно из теоретической механики, распределение скоростей в ней имело бы вид

			v = vo+ ω×		R,			(3.13)

где vo – скорость поступательного движения, а ω – вектор мгновенной уг-
ловой скорости. Таким образом, из формул (3.12) и (3.13) следует, что
то есть величина			F=	v−′	v ,
то есть величина	F представляет собой скорость деформации.
Замечание: совокупность точек O1, окружающих точку O, образует

частицу жидкости. За время dt точка O получает перемещение, равное vodt ,

			. Из рис. 3.1 видно, что R +
а точка O1 – равное v′dt			. Из рис. 3.1 видно, что R +				v′dt = R′ +	vodt или,
с учетом формулы (3.12),
							F)dt.
dR =		R′ −				+		(3.14)
dR =		R′ −	R = (v′ −	vo) dt = (ω × R		+		(3.14)

Полагая R′ =		ξ ′ , из формул (3.3) и (3.14) получаем
Полагая R′ =	e	ξ ′ , из формул (3.3) и (3.14) получаем
R′ = ekξ k′			= R + (v′ − vo )		dt = R + (R )v dt



*
Некоторые авторы под вихрем скорости понимают величину rot v =						2ω .

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ					53
или в координатном виде
ξ i′ =	ξ i +	ξ k	∂ vi	dt .	(3.15)

			∂ xk

На равенства (3.15) можно смотреть как на преобразование координат

точек жидкой частицы за время dt. Так как величины ∂ vi , как указыва-

∂ xk

лось, вычисляются в точке 0 и, следовательно, от ξ k не зависят, то преоб- разование (3.15) линейно. Поэтому за время dt этим преобразованием по- верхности второго порядка переводятся в поверхности второго порядка, плоскости – в плоскости, прямые линии – в прямые линии. Например, сфе- ра переходит в эллипсоид.

Обозначим

dR = R′ −

R (dR ≠

dR) ,

ε R =

(3.16)

Rdt

где ε R – относительное удлинение вектора R в единицу времени. Из фор-

мул (3.10), (3.11), (3.14) и (3.16) следует, что

RdR

R (ω

R+

ε R =

(3.17)

Rdt

R2dt

ε ikξξi

Так как ξ i

= α i

– направляющие косинусы вектора R, то

ε R = ε ikξ iξ k

ε ikα iα k =

2F(α j) ,

(3.18)

и относительное удлинение ε R не зависит от длины вектора а зависит

R ,

только от его направления.

Пусть ε R = 0. Тогда из равенства (3.17) следует, что


				ε R =	R		F =	Ro	F = 0 ,	(3.19)
				ε R =		2	F =		F = 0 ,	(3.19)
					R	2		R
					R			R
			1
	R
где Ro =		=		ekξ k – единичный вектор направления R . Так как соот-
где Ro =		=		ekξ k – единичный вектор направления R . Так как соот-
	R		R

ношение (3.19) справедливо при любом Ro , то с учетом формулы (3.11) получаем

F =		∂	F	=		= 0 ,
	ei				eiε ikξ k
		∂	ξ i

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

54		ГЛАВА III
и, следовательно, ε ikξ k = 0, откуда,	так как ξ k	произвольны, ε ik = 0 . Об-
ратное утверждение: если все ε ik =	0 , то ε ρ =	0 , и частица ведет себя как
абсолютно твердая.

Из приведенных рассуждений следует, что v* = F действительно яв-

ляется скоростью деформации.

Формула (3.12) может быть теперь переписана в виде

v′ = vm	+ v* = vo	+ ω × R + F

и представляет собой содержание первой теоремы Гельмгольца*: движение элементарного объема жидкости можно в каждый данный момент времени

				, рав-
представить разложенным на квазитвердое движение со скоростью vm				, рав-

			× R, и дефор-
ной сумме поступательной скорости	vo	и вращательной ω	× R, и дефор-
	=	F .
мационное движение со скоростью v*	=	F .

§2. Тензор скоростей деформаций

Рассмотрим скалярное произведение Из формулы и оп

R F . (3.11) -

ределения вектора R следует, что

			R F			∂	F	= ε ikξ iξ k .
			R F	= eiξ iek		∂		= ε ikξ iξ k .

						∂ ξ k
Так как скалярное произведение по своему смыслу инвариантно отно-
сительно преобразования координат, то
				ε ikξ iξ k =		ε~mnξ~mξ~n ,				(3.20)
где ξ i – координаты старой, а ξ~i					– новой систем координат.

Вектор	R	в старой		и	новой		системах координат			имеет вид
	~ ~	~	– орты новой системы координат. Умножив это со-

R = ekξ k =	ejξ j , где ej

отношение на ek , получим формулы преобразования координат
			~				~		~
		ξ k =			ξ jα jk	=	ξ mα mk =		ξ nα nk ,	(3.21)
		ξ k =	ejekξ j =		ξ jα jk	=	ξ mα mk =		ξ nα nk ,	(3.21)

где α jk – косинусы углов между осями новой и старой систем координат.

Подставив соотношения (3.21) в формулу (3.20), имеем

ε ikξ iξ k = ε ikξ~mα miξ~nα nk = ε~mnξ~mξ~n ,

а так как это равенство справедливо при любых ξ m ξ n , то

ε~mn = ε ikα miα nk .

(3.22)

* Герман Людвиг Фердинанд Гельмгольц (1821–1894), немецкий ученый, иностранный член-корреспон-

дент Петербургской Академии Наук.

Контакты | https://new.guap.ru/i03/contacts

1 / 461 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
10.01.20214.54 Mб79Гидродинамические исследования скважин Курс лекций.pdf
#
10.01.2021459.11 Кб18ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН НА ПРИОБСКОМ МЕСТОРОЖДЕНИИ.pdf
#
07.02.20211.03 Mб20ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН-1.pdf
#
10.01.2021353.18 Кб33Гидродинамические методы исследования скважин.pdf
#
02.01.202138.63 Mб20Гидродинамическое исследование скважин.pdf
#
02.01.202120.67 Mб24гидромеханика нефти.pdf
#
07.02.20211.34 Mб26Гидроочистка сырья.pdf
#
03.02.20211.46 Mб6гидроочистки сырья.pdf
#
24.01.2021452.97 Кб12Гидроразрыв пласта при КРС.pdf
#
24.01.2021271.57 Кб10Гидроразрыв пласта.pdf
#
29.01.2021304.86 Кб7Глубину превращения при термическом крекинге.pdf