гидромеханика нефти

СПБГУАП| Институт 4 группа 4736

Рис. 8.13

обращается в нуль, то есть в точках А и В конформность отображения на- рушается. Бесконечно удаленная точка плоскости z переходит в беско- нечно удаленную точку плоскости W. Направление скорости в бесконеч-

то есть преобразование Жуковского отображает внешность окружности

ружности с центром в точке (x, y) – несимметричный крылообразный профиль G – профиль Жуковского (рис. 8.14). Угол у задней кромки про- филей Жуковского равен 2π , что и является их отличительной особенно- стью.

* Николай Егорович Жуковский (1847–1921), один из основоположников современной аэромеханики.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

§5. Обтекание профиля произвольной формы

Пусть в комплексной плоскости ζ задан контур С. Требуется постро- ить его потенциальное обтекание так, чтобы в бесконечности движение было поступательным со скоростью Vζ , направленной под углом α к оси

Oξ . Угол α называется углом атаки (рис. 8.15).

плоскость комплексного переменного z и возьмем в плоскости z окруж- ность радиуса R (рис. 8.16). Определим функцию ζ = F(z) , дающую отображение внешности окружности S на внешность профиля С так,

ственным образом.

Будем считать, что функция ζ = F(z) известна. Так как контур С представляет собой линию тока, то окружность S – также линия тока. В соответствии с формулами (8.20) и (8.21) циркуляция Γ в плоскостях z и ζ имеет одно и то же значение.

Из формул (8.22) и (8.23) имеем

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

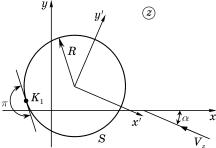
Рис. 8.16

Выберем систему координат x′Oy′ таким образом, чтобы ее начало совпадало с центром окружности S, а ось Ox′ была параллельна скоро- сти Vz . Тогда в соответствии с формулой (8.11) для циркуляционного об-

Функция W(z′) описывает обтекание в системе координат x′0y′. Пе- реходя от z′ к z путем поворота системы координат на угол α , получим комплексный потенциал W(z) .

Так как функция ζ = F(z) взаимно однозначная, то можно найти функ-

цию z = f(ζ ) и

W(z) = W(f( z) ) = W*( ζ ) ,

то есть, зная комплексный потенциал W(z) и функцию ζ = F(z) , можно построить комплексный потенциал обтекания контура C .

Предположим, что обтекаемый контур С имеет угловую точку К (рис. 8.15). Этой точке на окружности S соответствует точка К1 (рис. 8.16). Так как угол в точке К1 равен π , а в точке К больше π , то конформность отображения в точке К нарушается, и в этой точке ζ ′ = F′(z) = 0 .

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

откуда видно, что при dW ≠ 0 скорость в точке К обращается в беско- dz

нечность. Выше было показано, что это характерно для обтекания выступа и что это физически невозможно. Следовательно, в точке К1 должно вы-

полняться условие dW = 0 , то есть точка К1 должна быть критической. dz

Выбором величины циркуляции Γ можно добиться того, чтобы любая точка окружности S была критической, а также, чтобы в ней выполнялось

условие dW = 0 . Тогда скорость в точке К будет иметь конечное значе- dz

ние. Это требование было сформулировано в постулате Чаплыгина–Жуков- ского: циркуляция должна быть определена таким образом, чтобы в уг- ловой точке К скорость имела конечное значение.

Из формулы (8.16) видно, что при циркуляционном обтекании окруж- ности критические точки расположены так, что их стягивающая хорда параллельна Vz (рис. 8.17) и

рость на бесконечности Vζ могут задаваться произвольным образом*,

а циркуляция Γ определяется по формуле (8.27).

§6. Силы, действующие на профиль при стационарном обтекании

Пусть в плоскости z имеется некоторый контур С (рис. 8.18), обтекае-

ствии с интегралом Бернулли (7.28) равно (массовыми силами пренебрегаем)

* Для каждого профиля имеется предельное значение угла атаки, при превышении которого происходит срыв обтекания. Поэтому угол атаки можно задавать непревышающим этот предел.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

(обход контура С происходит против часовой стрелки, а давление направ- лено внутрь контура). Тогда с учетом формулы (8.28) будем иметь

C

Для преобразования формулы (8.30) заметим, что

dW dz = vxdx + vydy + i (vydx − vxdy) , dz

dW dz = vxdx + vydy − i (vydx − vxdy) . dz

Обтекаемый контур С представляет собой линию тока, а вдоль линии тока, как известно, vxdy − vydx = 0 . Поэтому вдоль контура С

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

170 ГЛАВА VIII

и формулу (8.30) можно представить в виде

C

Выражение (8.32) представляет собой первую формулу Чаплыгина*. Элементарный момент силы относительно начала координат (рис. 8.18)

дается выражением

dM = x dΥ − y dΧ = Re iz (dΧ − idΥ) ,

откуда с учетом равенства (8.29) и (8.31) после интегрирования по замкну- тому контуру С получаем вторую формулу Чаплыгина

Для вычисления интегралов в формулах (8.32) и (8.33) заметим, что

функция dW вблизи бесконечно удаленной точки представляет собой од- dz

нозначную аналитическую функцию. Поэтому она может быть разложена в ряд Лорана, а так как при z = ∞ она имеет конечное значение, то это раз- ложение имеет вид

Так как в соответствии с теоремой о вычетах интегралы по замкнуто- му контуру равны

∫ dzz = 2π i, ∫ dzzn = 0, n > 1,

CC

*Сергей Алексеевич Чаплыгин (1869–1942), один из основоположников аэромеханики. Действительный член АН СССР.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

то из формул (8.34) и (8.20) имеем

∫ dWdz dz = 2π iC1 = Γ + iQ .

C

Расход несжимаемой жидкости через замкнутый контур при отсутст- вии источников равен нулю, и, следовательно,

называется подъемной силой.

При безотрывном обтекании циркуляция в формулах (8.38) и (8.39) определяется из соотношения (8.27).

Подставив ряд (8.37) в формулу (8.33), после соответствующих пре- образований получаем

то есть получаем формулу для определения момента подъемной силы от- носительно начала координат.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Из формул (8.38) и (8.40) видно, что для вычисления подъемной силы и ее момента достаточно знать Vz , Γ и C2 , то есть достаточно знать пер- вые три члена разложения (8.34).

Заметим, что при циркуляционном обтекании контура, то есть при Γ ≠ 0 , модель идеальной жидкости позволяет вычислить величину подъемной силы, и результаты расчета достаточно хорошо согласуются с экспериментом. При Γ = 0 ËΡ = 0 – имеет место парадокс Даламбера.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Глава IX

ТЕЧЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ ПО ПРИЗМАТИЧЕСКИМ ТРУБАМ

Давно известно, что существуют две формы (два режима) течения жидкости. Первые фундаментальные исследования в этой области были опубликованы немецким ученым Г. Гагеном в 1839 и 1854 гг. Им было показано, что при течении воды в трубах существует режим, при кото- ром частицы жидкости движутся параллельно стенкам трубы, то есть жидкость движется несмешивающимися слоями. Для другого режима характерно перемешивание частиц жидкости в направлении, попереч- ном по отношению к оси трубы. Впоследствии указанные режимы те- чения были названы, соответственно, ламинарным и турбулентным.

Ламинарным течением называется течение, при котором траектории частиц жидкости представляют собой плавные кривые. Вид этих кривых определяется геометрией области течения. В частности, при течении по призматическим трубам траектории представляют собой прямые линии, параллельные образующим трубы. Из сказанного следует, что при лами- нарном течении жидкости по призматическим трубам вектор скорости должен быть направлен параллельно оси трубы.

Условие существования ламинарного режима течения было установ- лено Осборном Рейнольдсом в 1883 г. Ламинарный режим имеет место, если число Рейнольдса Re удовлетворяет условию

мический коэффициент вязкости жидкости, Reкр – критическое число Рей-

нольдса. Численное значение Reкр существенно зависит от геометрии об-

ласти течения.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

§1. Уравнения прямолинейного движения вязкой несжимаемой жидкости по призматическим трубам

Уравнения изотермического движения вязкой несжимаемой жидкости в общем случае имеют вид (4.42), или

dt

Введем систему координат Oxyz и направим ось Oz по оси рассматриваемой призматической трубы (рис. 9.1). Будем считать, что вектор скоро- сти течения направлен параллельно оси трубы, то есть, что

Необходимо особо отметить, что из-за отсутствия конвективных чле- нов уравнение (9.3) является линейным, что существенно упрощает про- блему его интегрирования. Проектируя уравнение (9.3) на оси координат,

падают с уравнениями (6.2). Следовательно, в плоскости xOy, перпендику- лярной оси трубы, имеет место гидростатический закон распределения давления.

Так как u = u(x, y, t) , то из последнего уравнения (9.4) следует, что

∂ p = f(x, y, t) .

∂ z

Контакты | https://new.guap.ru/i03/contacts