гидромеханика нефти

Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

e1V(t) . Тогда равенство (7.69) при-

( ϕ ) 2 = f( t) .

.pdf

Скачиваний:

Добавлен:

02.01.2021

Размер:

20.67 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 469 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

125

При установившемся движении расход вдоль трубки тока в соответст- вии с равенством (2.41) постоянен ( v1S1 = v2S2 ), и, следовательно, при су- жении трубки скорость растет, а давление падает. По этому принципу дей- ствуют водоструйный насос, пульверизатор и другие устройства.

Перейдем к рассмотрению установившегося движения идеального не- вязкого газа. Его уравнение состояния – уравнение Клапейрона – имеет

вид
	p	= RT ,	(7.30)

	ρ

где R – газовая постоянная, T – абсолютная температура.

Из формул (7.17) и (7.30) видно, что для вычисления функции давле-

ния необходимо задать термодинамический процесс.
Из уравнения притока тепла (7.4) имеем
		qe dt = du −	p	dρ =	du + pd			1	= du +	p dV ,	(7.31)
		qe dt = du −		dρ =	du + pd				= du +	p dV ,	(7.31)
			ρ 2					ρ
где V =	1	– удельный объем. Таким образом, для невязкого газа уравне-
где V =		– удельный объем. Таким образом, для невязкого газа уравне-
	ρ
ние притока тепла совпадает с первым началом термодинамики.
При ρ = const V = const , и
			qedt =		CV dT = du ,						(7.32)
где CV – теплоемкость при постоянном объеме. При										p = const	из фор-
мул (7.30) и (7.32) имеем
		qedt = CPdT = du + d				p	= CV dT + R dT ,
		qedt = CPdT = du + d					= CV dT + R dT ,
откуда следует формула Майера*						ρ
откуда следует формула Майера*
				R =	CP − CV ,						(7.33)

где Cp – теплоемкость при постоянном давлении.

Подставив в уравнение (7.31) уравнение состояния (7.30) и учитывая равенства (7.32) и (7.33), получим

qedt =

CV dT +

kpd

CP −

k −

(7.34)

ρ k− 1 k p

1 dp

ρ k− 1

k− 1

k ,

− 1

k −

где k =

– показатель адиабаты.

* Юлиус Роберт Майер (1814–1878), немецкий естествоиспытатель и врач. Показал эквивалентность ме- ханической работы и теплоты.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

126

ГЛАВА VII

При адиабатическом процессе, то есть при отсутствии притока тепла извне, qe = 0 , и

p		= Θ		p	=	ρ	k
			или					(7.35)
	k
ρ				p0		ρ 0	.

Заметим, что при выводе соотношения (7.35), называющегося адиа- батой Пуассона*, использовалось уравнение притока тепла (7.31) для иде- альной жидкости. Следовательно, адиабата Пуассона справедлива при адиа- батическом процессе без трения.

Покажем, что адиабатический процесс без трения является изэнтро- пическим, то есть что при этом процессе энтропия сохраняет постоянное

значение.
Энтропия s , как известно, определяется соотношением
ds =	dq	.	(7.36)

	T
Пусть в рассматриваемом объеме жидкости тепло поступает только
извне, то есть dq = qedt . Тогда в соответствии с уравнением состояния

(7.30) и формулами (7.33), (7.34) и (7.36) имеем

ds =

qedt

= CV

(CP

− CV ) ρ d

(k −

1) d ln

CV d ln T +

= CV d ln

ρ k−

Тогда

k− 1

ρ 1

s −

s = CV ln

CV ln

(7.37)

ρ 2

= s1

При изэнтропическом процессе s2

и из равенства (7.37) имеем

ρ 1

0 ,

или

(7.38)

ρ 2

Из формул (7.35) и (7.38) следует, что адиабатический процесс без трения, действительно, является изэнтропическим.

В общем случае неадиабатического процесса уравнение притока те- пла (7.31) можно с учетом равенств (7.30), (7.32) и (7.33) представить в виде

qedt = CdT = CV dT + pd ρ1 ,

* Симон Дени Пуассон (1781–1840), французский математик и физик. Иностранный почетный член Пе- тербургской Академии Наук.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ									127
или
	C −	CV	d	p	−	pd	1	= 0 ,	(7.39)
	CP −		d		−	pd	ρ	= 0 ,	(7.39)
	CP −	CV		ρ			ρ

где C – теплоемкость при рассматриваемом термодинамическом процессе. Обозначив

C − CV

n ≠ 1,

CP − CV

n −

из соотношения (7.39) получим

− 1

npd

n − 1

n = 0 ,

откуда

p =

Aρ n .

(7.40)

Соотношение (7.40) представляет собой уравнение политропического процесса. В общем случае величины A и n (через теплоемкость C) могут меняться от частицы к частице, что определяется характером подвода теп- ла и свойствами частиц (при неоднородной жидкости). Следовательно, A и n являются функциями лагранжевых координат частицы Xj и t . При

установившемся движении линия тока совпадает с траекторией, и если бы A и n зависели от Xj , то давление в фиксированной точке линии тока

(пространства) менялось бы со временем, то есть движение было бы неус- тановившимся. Следовательно, A и n при установившемся движении мо- гут зависеть только от L.

Если параметры A и n имеют одни и те же значения во всей облас- ти, занятой жидкостью, то политропический процесс будет баротроп- ным.

Воспользовавшись для вычисления функции давления Ρ формула-

ми (7.17), (7.30), (7.33), (7.35) и (7.40), получим для адиабатического про-

цесса с точностью до постоянных интегрирования выражения

ρ k− 1 =

1 k− 1

Ρ =

= CPT ,

(7.41)

k p k

k −

1 ρ

а для политропического процесса – выражения

Aρ n− 1 =

n− 1

(7.42)

An p n

n −

1 ρ

Для изотермического процесса

RT0 =

const ,

(7.43)

ρ 0

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

128 ГЛАВА VII

где p0, ρ 0 – давление и плотность при температуре T0 , и из равенств (7.17) и (7.43) имеем

Ρ =	p0	ln	p	=	p0	ln	ρ	.	(7.44)
	ρ 0				ρ 0
			p0				ρ 0
Подставив соотношение (7.41) в равенство (7.21) и полагая Π									= − gz ,

получим следующие виды интеграла Бернулли для адиабатического процесса:

gz +

C = const ,

(7.45)

k − 1 ρ

k−

gz +

k p k

C =

const ,

(7.46)

− 1

gz +

ρ k− 1 +

C =

const ,

(7.47)

k −

gz +

CpT +

C =

const .

(7.48)

Для политропического процесса из формул (7.21) и (7.42) имеем

gz +

C =

const,

n ≠ 1,

(7.49)

n −

1 ρ

n −

gz +

An p n

C =

const,

n ≠

(7.50)

n −

gz +

Aρ n −

C =

const,

n ≠

(7.51)

n −

Для изотермического процесса из равенств (7.21) и (7.44) получаем

gz +

const ,

(7.52)

ρ 0

gz +

const .

(7.53)

ρ 0

Из формул (7.45)–(7.51) видно, что при адиабатическом и политропи-

ческом процессах величины

, p,

ρ с ростом скорости уменьшаются. При

адиабатическом процессе с ростом скорости уменьшается также абсолют- ная температура T . При изотермическом процессе, как это следует из фор- мул (7.43), (7.52) и (7.53), с ростом скорости величины p и ρ уменьшают-

ся, а отношение ρ остается постоянным.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

129

§4. Простейшие примеры приложения интеграла Бернулли

Рассмотрим некоторые простейшие примеры приложения интеграла Бернулли к течениям идеальной несжимаемой жидкости в поле сил тяжести.

1. Истечение жидкости из ма- лого отверстия в сосуде. Будем счи- тать, что S0 >> S, где S0 – площадь свободной поверхности жидкости, S – площадь отверстия в сосуде (рис. 7.1). Тогда скоростью измене- ния уровня в сосуде можно пренеб-

речь и считать, что z0 = const .							Рис. 7.1
речь и считать, что z0 = const .
Из формулы (7.28) имеем
gz0 +	p0	= gz +	p	+	v2	,	(7.54)
gz0 +	ρ	= gz +		+	2	,	(7.54)
	ρ		ρ		2
где p0 – давление на свободной поверхности,					z,		p, v – параметры струи

на выходе из отверстия. Из формулы (7.54) следует, что скорость истече- ния из отверстия равна

v = 2gh + 2	p0 − p	,	(7.55)
	ρ

где h = z0 − z . Если p0 = p , то из формулы (7.55) имеем известную фор- мулу Торричелли

v = 2gh ,

то есть скорость истечения равна скорости падения тяжелого тела с высоты h . Так как на поверхности вытекающей струи p = const , то из интегра-

ла Бернулли следует, что с опусканием струи ее скорость растет. 2. Скоростная трубка (трубка

Пито). Пусть в жидкости находится осесимметричное тело, направление оси которого совпадает с направ- лением скорости течения (рис. 7.2). В точке A, расположенной на доста- точном расстоянии от носика тела В, скорость равна vA , а давление – pA .

В точке В скорость vB = 0 , линии	Рис. 7.2
тока разветвляются. Таким образом,

точка В является особой. Можно считать, что в точке С, также достаточно удаленной от точки В, возмущения потока, вызванные носиком трубки, исчезли, так что vC = vA , pC = pA (для простоты предполагается, что по- ток направлен горизонтально).

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

130

ГЛАВА VII

Записав уравнение (7.28) для линии тока АВ, имеем

vA2

откуда

pB − pA

vA = vC = 2

2 pB −

(7.56)

Таким образом, измерив разность давлений

pB −

pC ,

можно определить

скорость vA .

На практике в формулу (7.56) вводится поправочный коэффициент скорости ϕ , учитывающий искажение потока и наличие сил трения. Ко- эффициент ϕ определяется путем градуировки, и для хороших трубок

ϕ = 0,99–1,02.

3. Водомер Вентури. Выберем в труб- ке (рис. 7.3) сечения I – I и II – II и бу- дем считать, что скорости в этих сече- ниях распределены равномерно, то есть,

что там		∂ vj	= 0 . Тогда из уравнения

		∂ xi
Эйлера (7.2) следует, что при устано-
вившемся течении в каждом из этих се-
чений
	p = ρ g , то есть давления рас-
пределены по гидростатическому зако-
ну*
Рис. 7.3		ρ gz + p= const .		(7.57)

Будем обозначать все величины, относящиеся к сечению I – I, индек- сом 1, а к сечению II – II – индексом 2. Запишем для линии тока, проходя- щей по оси трубы, интеграл Бернулли (7.28)

gz1 +	p1	+	v12	= gz2 +	p2	+	v22	.	(7.58)
	ρ		2		ρ		2

Так как скорости распределены по сечениям равномерно, то в соответст- вии с уравнением неразрывности (2.41)

v1S1 = v2S2 = Q .

(7.59)

* Этот же вывод следует из уравнения Навье–Стокса (4.42).

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

131

Из равенств (7.58) и (7.59) следует, что

g(z1 − z2) +

p1 − p2

2 −

(7.60)

С другой стороны, из формулы (7.57) имеем

ρ gzA + pA =

ρ gz1 +

p1 ,

ρ gzB +

pB = ρ gz2

+ p2 ,

(7.61)

где индексы А и В относятся к отверстиям А и В.

Подставив соотношения (7.61) в формулу (7.60), получим

Q = S S

g(zA − zB)

+ pA − pB

(7.62)

1 2

S12

− S22

pA − pB ,

Из формулы (7.62)

видно, что, измерив разность давлений

можно определить расход Q. При практическом использовании формулы

(7.62) в нее вводится поправочный коэффициент расхода

, учитывающий

неравномерность поля скоростей в сечениях и наличие сил трения.

§5. Интеграл Коши–Лагранжа

Для вывода интеграла Коши-Лагранжа, представляющего собой ана- лог интеграла Бернулли для случая неустановившегося движения, примем следующие предположения:

	=	ϕ ;
а) течение потенциальное, v	=	ϕ ;	= Π ;

б) напряжение массовых сил обладает потенциалом, F
в) процесс баротропный, p =		p(ρ ) .

Последнее требование обусловлено тем, что при неустановившемся движении линии тока не совпадают с траекториями. Следовательно, нельзя считать, что p = p(L, s), ρ = ρ ( L, s) и исключать s , как это было сделано

при выводе интеграла Бернулли. Поэтому для небаротропного движения в общем случае не представляется возможным вычислить функцию давления Ρ .

0 , и уравнение Эйлера в форме

При сделанных предположениях rot v

Громеко–Ламба (7.13) принимает вид

−

Ρ ,

(7.63)

∂

v +

∂ t

где функция давления Ρ вычисляется по формулам (7.18).

Так как

∂ ( ϕ )

= ∂ ϕ ,

∂ v

∂ t

то уравнение (7.63) может быть переписано в виде

∂ ϕ

−

Π +

Ρ +

(7.64)

∂ t

= 0 .

Поскольку оператор Гамильтона

содержит только пространствен-

ные производные, а функции, входящие в равенство (7.64), в общем случае

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

132						ГЛАВА VII
зависят от времени, то из равенства (7.64) имеем
	∂ ϕ	− Π	+ Ρ +	v2	= f(t) .	(7.65)
		− Π	+ Ρ +		= f(t) .	(7.65)
	∂ t		2

Равенство (7.65) называется интегралом Коши-Лагранжа. Из его вы- вода следует, что функция f(t) имеет один и тот же вид во всей области, занятой жидкостью. При установившемся движении интеграл Коши–Лагран- жа переходит в интеграл Бернулли (7.27) для случая баротропного потен- циального движения.

Для определения функции f (t) необходимо знать движение в какой- либо одной точке жидкости, например, на границе области.

Введем вместо потенциала ϕ функцию ϕ 1 , определенную равенством

ϕ 1 = ϕ + ∫ f(t) dt .

Тогда

∂ ϕ 1

∂ ϕ

+ f(t) ,

ϕ 1 = ϕ ,

∂ t

и интеграл Коши–Лагранжа можно переписать в виде

∂ ϕ 1

− Π

+ Ρ +

= 0 .

∂ t

Для несжимаемой жидкости в поле сил тяжести интеграл Коши–Ла-

гранжа имеет вид

∂ ϕ 1

+ gz +

0 .

(7.66)

∂ t

Для идеальных газов при изэнтропическом процессе в соответствии

с формулой (7.37) имеем

∂ ϕ 1

+ gz +

= 0 .

∂ t

k −

1 ρ

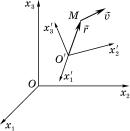
В ряде случаев рассматриваемое движе- ние в неподвижной системе координат удоб- нее описывать в подвижной системе коорди- нат. Пусть, кроме неподвижной системы ко- ординат Ox1x2x3 , имеется подвижная систе-

ма O′x1′x2′x3′ (рис. 7.4). Фиксирование значе- ний x′j означает фиксирование положения

точки М относительно подвижной системы. Если известен закон движения точки М

относительно неподвижной системы коор-

Рис. 7.4	динат, то*	= xi (x′j , t).	(7.67)
	xi


* Напомним, что сокращенная запись xi (x ′j , t ) означает xi = xi (x1 , x 2 , x 3 , t) , j =			1, 2, 3.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ							133
Тогда при фиксированных значениях x′j
	∂ xi	=	∂ xi (x′j	, t)	=	vi пер ,	(7.68)
	∂ t	=	∂ t		=	vi пер ,	(7.68)
	∂ t		∂ t

где vi пер – проекции скорости переносного движения vпер . По формуле
Эйлера
	vÔÂ = v0′+			ω×		r ,
где v0 – скорость начала координат O′, ω						– мгновенная угловая скорость

вращения координатной системы O′x1′x2′x3′ , r –							радиус-вектор точки М
в этой системе.
В неподвижной системе Ox1x2x3 потенциал скоростей зависит от xi , t –
ϕ = ϕ (xi , t) . Подставив в это выражение закон движения (7.76), получим
потенциал ϕ I = ϕ [xi (xj , t)] ,		выраженный				через	координаты подвижной

системы. Тогда

∂ ϕ I

∂ ϕ

∂ xi

∂ t

∂ xi

∂ t

или, с учетом формул (7.68),

∂ ϕ I

∂ ϕ

vпер

vперv .

∂ t

Теперь интеграл Коши–Лагранжа (7.65) может быть представлен в виде

∂ ϕ I	−		− Π
		vперv
∂ t		vперv
∂ t

Положим что система 0′x1′x2′x3′

системы 0x1x2x3 со скоростью vпер нимает вид

∂ ϕ I	−		− Π + Ρ +	v2	=	∂ ϕ I
		e1Vv
∂ t		e1Vv		2		∂ t

+ Ρ +	v2	= f(t) .	(7.69)

2

движется относительно неподвижной

§6. Теорема Томсона

Возьмем в жидкости некоторую линию АВ и будем считать, что все ее точки движутся вместе с жидкостью, то есть что АВ – жидкая линия. Ее


уравнение можно представить в виде r =			r(s, t) , где s – некоторый пара-
метр,		изменяющийся вдоль линии, например, длина дуги. При s = const
		(t) – закон движения какой-либо точки жидкой линии АВ.
r =	r

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

134 ГЛАВА VII

Рассмотрим циркуляцию скорости
Γ = ∫ v dr ,	(7.70)

AB
взятую вдоль АВ и вычислим производную	dΓ	. При этом необходимо учи-
взятую вдоль АВ и вычислим производную		. При этом необходимо учи-
	dt

тывать, что с течением времени меняется на только скорость точек, обра- зующих линию АВ, но и вид самой линии АВ.

Вычислим предварительно производную по времени от интеграла, взя- того вдоль жидкой линии. С учетом определения интеграла имеем

d lim

∞

lim dϕ i

d∆ ri

ϕ i ∆ ri

∆ ri + ϕ

dt ∫

dt ∆

∑

r →

∆

r →

0 dt

i = 1

Так как ∆

0∆ s ,

где

0 –

единичный вектор касательной к АВ

(рис. 7.5), то

d∆

−

∂ v

(7.71)

vBi

vAi

∂ s

∫ ϕ

dr =

∫

dr +

∫ ϕ

∂

ds .

(7.72)

∂ s

Рис. 7.5

Полагая в формуле (7.72) ϕ

, из формулы (7.70) имеем

∂

1 ∂

∫

∫ v

ds = ∫

∫

ds =

∂ s

(7.73)

(vB2 − vA2 ) .

dr +

∫ dr

Контакты | https://new.guap.ru/i03/contacts

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 469 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
10.01.20214.54 Mб82Гидродинамические исследования скважин Курс лекций.pdf
#
10.01.2021459.11 Кб19ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН НА ПРИОБСКОМ МЕСТОРОЖДЕНИИ.pdf
#
07.02.20211.03 Mб21ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН-1.pdf
#
10.01.2021353.18 Кб33Гидродинамические методы исследования скважин.pdf
#
02.01.202138.63 Mб20Гидродинамическое исследование скважин.pdf
#
02.01.202120.67 Mб24гидромеханика нефти.pdf
#
07.02.20211.34 Mб28Гидроочистка сырья.pdf
#
03.02.20211.46 Mб6гидроочистки сырья.pdf
#
24.01.2021452.97 Кб12Гидроразрыв пласта при КРС.pdf
#
24.01.2021271.57 Кб11Гидроразрыв пласта.pdf
#
29.01.2021304.86 Кб7Глубину превращения при термическом крекинге.pdf