Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

гидромеханика нефти

.pdf

Скачиваний:

Добавлен:

02.01.2021

Размер:

20.67 Mб

Скачать

☆

<<< < Предыдущая 12 / 462 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

Выражение (3.22) представляет собой определение аффинного орто- гонального тензора второго ранга. Таким образом, скорости деформаций

представляют собой симметричный (ε ik =		ε ki ) тензор второго ранга, ком-
поненты которого задаются матрицей
ε11	ε12	ε13
D = ε 21	ε 22	ε 23 .
ε 31	ε 32	ε 33

§3. Физический смысл компонент тензора скоростей деформаций

Для выяснения физического смысла компонент тензора скоростей де-

формаций ε ik рассмотрим вектор R, параллельный оси Ox1. Для этого век- тора направляющие косинусы равны α 1 = 1, α 2 = α 3 = 0, и из формулы (3.18) в этом случае имеем ε R = ε11 . Следовательно, ε11 представляет собой ско- рость относительного удлинения вектора, параллельного оси Ox1.

Аналогично можно показать, что ε kk

– скорости относительного удлине-

ния вдоль соответствующих координатных осей.

Положим,

что

поступательная

и вращательная скорости жидкой час-

тицы

отсутствуют.

Рассмотрим век-

тор R, лежащий в

плоскости

x1Ox2

(рис. 3.2). За время dt этот вектор пре-

образуется в вектор R′,

который мо-

жет и не лежать в плоскости x1Ox2. То-

гда (рис.

3.2)

Fdt.

O1O1

v dt

векто-

Разложим

вектор

v dt

на

ры

O1O2

Ë O2O1 так,

чтобы вектор

O1O2

был перпендикулярен R и ле-

Рис. 3.2

жал в плоскости x1Ox2. Очевидно, что

O O = v*dt , v

* – составляющая вектора v* в плоскости x Ox .

v1′ dt , то

Так как O1O2 = R dϕ

dϕ

v1*

n F 1∂ F 1 ∂ F

∂ ϕ

R ∂ n R2

– единичный вектор, направленный по O1O2 .

где n

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

56 ГЛАВА III

x1Ox2

ξ 1 = Rcos ϕ ,

В плоскости

координаты вектора R равны

ξ 2 =

Rsin ϕ , ξ 3

0 , и в соответствии с формулой (3.10)

F =

(ε11ξ 12 + 2ε12ξ 1ξ 2 + ε 22ξ 22) =

R2 (ε11 cos2 ϕ

+ ε12 sin 2ϕ

ε 22 sin2 ϕ ),

откуда

dϕ

(ε 22

−

ε11) sin 2ϕ +

ε12 cos 2ϕ .

(3.23)

Рассмотрим

вектор

R и

лежащий

в плоскости x1Ox2. Тогда

ϕ 1 =

ϕ +

и, как следует из формулы (3.23),

dϕ 1 = − dϕ . Следовательно,

векторы

R и R1

либо расходятся, либо сходятся, но всегда вращаются

в противоположные стороны. Скорость γ изменения угла между вектора-

ми

R и

R1, очевидно,

равна γ

= 2

dϕ

ϕ = 0 , как это следует из

. При

(3.23), γ

2ε12 .

формул

Итак,

ε12 представляет собой половину скорости скашивания коорди-

натного угла в плоскости x1Ox2. Аналогичное значение имеют в соответст-
вующих плоскостях компоненты ε ik(i ≠ k) .
	Рассмотрим	в	качестве	примера		течение
	с полем скоростей v1		= 0, v2 = kx3 , v3			= 0 . Оче-
	видно, что в этом случае бесконечно малый
	квадрат ОАВС (рис.		3.3) за время		t	с точно-
	стью до малых	второго порядка			превратится
	в ромб ОА1В1С. В соответствии с формулами (3.5)
	для заданного поля скоростей имеем
	ε11 = ε 22 = ε 33 = ε12 = ε13 = 0,				ε 23	=	k	.

						2
Рис. 3.3	Следовательно, скорость скашивания прямо-
	го угла АОС равна γ		= 2ε 23 =	k.

§4. Тензорная поверхность симметричного тензора второго ранга

Рассмотрим поверхность второго порядка с центром в начале коорди- нат. Ее уравнение, как известно из курса аналитической геометрии, имеет

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

вид

aijxixj = 1	, aij = aji ,	(3.24)
где xi – декартовы координаты, aij	– коэффициенты поверхности второго

порядка. При переходе из одной системы координат в другую, декартовы координаты преобразуются по правилу

xi = α ki x~k	, xj = α lj x~l ,
и в новой системе координат уравнение (3.24) запишется в виде
aijα kiα ljx~kx~l =	a~mnx~mx~n = 1	(3.25)

где a~mn – коэффициенты поверхности второго порядка в новой системе координат.

Из формулы (3.25) следует, что коэффициенты поверхности второго порядка в новой и старой системах координат связаны между собой равен- ствами

a~mn = aijα miα nj ,

то есть коэффициенты aij поверхности второго порядка (3.24) представ-

ляют собой симметричный тензор второго ранга.

Итак, каждому симметричному тензору второго ранга можно поста- вить в соответствие поверхность второго порядка вида (3.24) и, наоборот, всякой поверхности второго порядка вида (3.24) можно поставить в соот- ветствие симметричный тензор второго ранга. Поверхность aijxixj = 1 на-

зывается характеристической поверхностью тензора второго ранга или

тензорной поверхностью.

В курсах аналитической геометрии доказывается, что у всякой поверх- ности второго порядка вида (3.24) имеется по меньшей мере три таких вза- имно-ортогональных направления, приняв которые за оси координат, квадратичную форму a x x приводят к каноническому виду. Эти направ-

ления называются главными или собственными направлениями, а коорди- натные оси – главными осями тензорной поверхности.

Уравнение тензорной поверхности (3.24) в главных осях имеет вид

(a x2		+	a x2			+	a x2 ) = 1,		(3.26)
1	1			2	2		3	3
матрица тензора aik –
		a			0		0
			1
		0			a2		0	.
			0		0		a3
			0		0		a3

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ГЛАВА III

Компоненты тензора aij , записанного в главных осях, называют глав-

ными компонентами и обозначаются одним индексом.

Главные оси тензорной поверхности в общем случае, как это следует из теоремы Гельмгольца, вращаются с мгновенной угловой скоростью ω .

Рассмотрим скорости деформаций бесконечно малой сферической частицы

ξ 12

ξ 22 +

ξ 32

(3.27)

За время dt она преобразуется в эллипсоид вида*

′2

′

′2

ξ 1

ξ 2

ξ 3

= 1.

(3.28)

R(1 + ε1dt) ,

В соответствии с ранее доказанным, полуоси эллипсоида равны a =

b = R(1 + ε 2dt)

, c = R(1 + ε 3dt) .

Скорость Θ

объемного расширения частицы равна

Θ = lim

V′ −

abc

−

π R3

ε 1 + ε 2 + ε 3

∂ vi

lim

div v ,

π R3

∂ xi

∆ t → 0

где V′ – объем эллипсоида (3.28), V – объем шара (3.27). Из определения

скорости объемного расширения очевидно, что Θ и div являются инва- v

риантами относительно преобразования координат.

§5. Циркуляция скорости. Потенциальное движение жидкости

Рассмотрим в объеме, занятом движущейся жид- костью, некоторую линию АВ и в каждой ее точке по-

строим вектор v (рис. 3.4). Скалярное произведение v ds , где ds – элемент линии АВ, не зависит, очевид- но, от выбора координат. Величина

Γ = ∫ vds =	∫ vsds	(3.29)

AB	AB

Рис. 3.4 называется линейным интегралом вектора v вдоль кри- вой АВ или циркуляцией скорости вдоль этой кривой.

При интегрировании от В до А или при изменении направления об- хода при интегрировании по замкнутой кривой, знак циркуляции меня-

* Главные оси эллипсоида могут не совпадать с координатными осями Oxi за счет деформации поворота.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

ется на обратный. Из этого следует, что циркуляция по замкнутому кон- туру (рис. 3.5) равна сумме циркуляций по контурам I и II, так как вдоль линии АВ интеграл (3.29) вычисляется дважды, причем в противополож- ных направлениях.

В соответствии с теоремой Стокса* циркуляция

скорости v по замкнутому контуру L равна удвоен- ному потоку вихря ω сквозь поверхность S, натяну- тую на этот контур, то есть

Γ =					=	2∫ ω n ds .
Γ =	∫ vds	= 2∫ ω		ds	=	2∫ ω n ds .	(3.30)
	L		S			S
Если существует функция ϕ (xj , t) , удовлетворяю-
щая условию
	vi =	∂ ϕ			=	ϕ ,	(3.31)
		∂ ϕ	,	v				Рис. 3.5
			,	v				Рис. 3.5
		∂ xi
то течение называется потенциальным, а функция ϕ								– потенциалом скоро-

стей. В курсах математического анализа доказывается, что для существо- вания потенциала скоростей необходимо и достаточно, чтобы

∂ vi

−

∂

= 0,

i ≠

j .

(3.32)

∂ xj

∂

Вихрь скорости ω , по определению, равен

∂

ω =

rot v

(3.33)

∂ x1

∂ x2

∂ x3

= 0, и наоборот,

и из формул (3.36) и (3.37) следует, что если v

то ω

= 0, то есть отсутствие

если ω

= 0, то v

= ϕ . Это значит, что условие ω

вихрей, необходимо и достаточно для существования потенциального те-

чения.			=

Так как элемент кривой АВ ds				ekdxk , то при потенциальном тече-
нии в соответствии с формулами (3.31) и (3.32), имеем
Γ = ∫ vds =	B	∂ ϕ ekdxk =	B	∂ ϕ dxi =	B
Γ = ∫ vds =	∫ ei	∂ ϕ ekdxk =	∫	∂ ϕ dxi =	∫ dϕ = ϕ (B) − ϕ ( A) . (3.34)

AB	A	∂ xi	A ∂ xi		A

Следовательно, в этом случае циркуляция скорости зависит только от положения начальной и конечной точек кривой АВ и не зависит от пути интегрирования.

* Джордж Габриэль Стокс (1819–1903), английский физик, математик и гидромеханик.

Контакты | https://new.guap.ru/i03/contacts

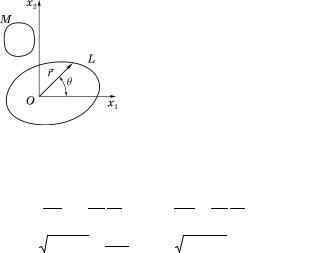
СПБГУАП| Институт 4 группа 4736

ГЛАВА III

Если потенциал ϕ неоднозначен, то циркуляция по замкнутому конту- ру L отлична от нуля. Это может произойти, когда внутри области, ограни- ченной контуром L, существуют вихри.

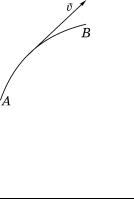
При потенциальном течении циркуляция по замкнутому контуру L не равна нулю только в том случае, если контур L не может быть стянут в точку непрерывным преобразованием, то есть в том случае, если область внутри L многосвязна (рис. 3.6). В многосвязной области потенциал может быть неоднозначным.

В качестве примера рассмотрим течение с потенциалом скоростей

ϕ =	J	θ	=	J	arctg	x2	.	(3.35)
	2π			2π
						x1
На контуре M функция ϕ			однозначна, а на L – многозначна (рис. 3.7).

После обхода точки O потенциал ϕ получает приращение, равное 2π m, где m – число обходов вокруг точки O. Точка O – начало координат – особая. По- тенциал сохраняет в ней конечное значение, но это значение зависит от пу- ти, по которому совершается подход к точке O.

	Рис. 3.6							Рис. 3.7
Из формулы для потенциала скоростей имеем
v1	=	∂ ϕ = −	J x2	,	v2 =	∂ ϕ =	J x	, v3 = 0 ,
		∂ x1	2π r2			∂ x2	2π r2
v =		v12 + v22 = J		,	r =	x2 + x22 .
			2π	r
	=	ϕ перпендикулярен линии ϕ = const и направлен в сто-
Вектор v	=	ϕ перпендикулярен линии ϕ = const и направлен в сто-

рону возрастания функции ϕ = ϕ (θ ) . Линии тока – окружности с центром в начале координат (рис. 3.8).

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ СРЕДЫ

При r → 0 v → ∞ , то есть начало координат – особая точка поля ско-

ростей. В этой точке производные	∂ ϕ		∂ ϕ		терпят разрыв, и, следователь-
ростей. В этой точке производные		,			терпят разрыв, и, следователь-
	∂ x		∂ x	2
	1			2

но, нарушаются условия теоремы Стокса. Если же точку r = 0 исключить, то область становится многосвязной. Особую точку можно рассматривать как концентрированный вихрь.

Циркуляция по окружности С с центром в точке 0 равна

	2π
Γ = ∫ vdr =	∫ vrdϕ	= 2π rv =	J .
C	0
Циркуляция по любой замкнутой кривой С1, охватывающей начало ко-
ординат, равна J. Действительно,	Γ C1 =	Γ BA + Γ C +	Γ AB = Γ C , где индексы

указывают на линии, вдоль которых выполняется интегрирование (рис. 3.9).

Рис. 3.8 Рис. 3.9

Рассмотрим поле вихря ω . Для этого поля можно построить вектор- ные линии* – линии вихря. Аналогично трубке тока можно построить вих-

ревые трубки и их живые сечения (рис. 3.10).
Из формулы (3.33) следует, что div ω =			0	и в соответствии с теоре-
мой Гаусса–Остроградского	∫ ω	n ds =	∫ ω	nds =	0 ,	(3.36)
∫ div ω dV =

V	S	S
то есть поток вихря через замкнутую поверхность равен нулю.
Рассмотрим вихревую трубку, ограниченную поперечными сечения-
ми S1 , S2 и боковой поверхностью S3 (рис. 3.10). По определению вихре-
вой трубки, ω n = 0 на S3 , и из формулы (3.36) имеем
∫ ω nds =	∫ ω nds + ∫ ω nds = 0 .				(3.37)
S	S1	S2

* См. гл.I, § 4.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

62							ГЛАВА III
	Меняя на S1 направление нормали на проти-
	воположное* и используя теорему Стокса (3.30),
	из формулы (3.37) получаем
				1			1
	∫ ω nds =	∫ ω	nds =	1	∫ vds =		1	Γ . (3.38)
	∫ ω nds =	∫ ω	nds =		∫ vds =			Γ . (3.38)
	S	S		2 C		2
	1	2
	Из формулы (3.38) следует, что циркуляция
	по любому замкнутому контуру С, охватываю-
	щему вихревую трубку, есть величина постоян-
Рис. 3.10	ная. Этот вывод представляет собой вторую тео-
Рис. 3.10	рему Гельмгольца.
	рему Гельмгольца.
Для элементарной вихревой трубки из равенства (3.38) имеем
	2ω 1∆ S1 = 2ω 2 ∆ S2 =	Γ	,			(3.39)
где S1 , S2 – площади сечений вихревой трубки. Величина 2ω ∆						S называ-

ется напряжением вихревой трубки.

Из равенства (3.39) следует, что если величина ω во всей области жидкости конечна, то и ∆ S в этой области конечна. Следовательно, вихре- вые трубки не могут кончаться внутри жидкости. Они либо замкнуты, либо оканчиваются на поверхности жидкости, либо уходят в бесконечность. Очевидно, что этот вывод справедлив и для трубок тока.

* При использовании теоремы Стокса направление обхода на контурах, ограничивающих сечения S1

и S2 , должно быть одинаковым. Поэтому если на S2 берется нормаль внешняя, то на S1 необходимо взять внутреннюю.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Глава IV

ЖИДКОСТИ

§1. Математическая модель идеальной жидкости

Как уже указывалось в §2.9, система уравнений сплошной среды (2.90) является незамкнутой. Для ее замыкания необходимо добавить реологиче- ское уравнение рассматриваемой сплошной среды или, иначе говоря, за- дать свойства этой среды. Простейшей моделью сплошной среды является идеальная жидкость.

Идеальной жидкостью (газом) называется изотропная сплошная среда, в которой отсутствуют касательные напряжения, то есть pik = 0 (i ≠ k) . При этом нормальные напряжения являются сжимаю- щими и их величина зависит только от точки сплошной среды и не зави-

сит от направления. Касательные напряжения в жидкости возникают бла- годаря трению. Поэтому можно сказать, что идеальная жидкость – это жидкость, лишенная внутреннего трения.

Пренебрежение внутренним трением существенно упрощает матема- тическую постановку задач гидромеханики. Это в ряде случаев помогает разобраться в физике рассматриваемых процессов. Кроме того, модель идеальной жидкости позволяет достаточно хорошо описать такие важные с точки зрения практики, явления как гидравлический удар, возникновение ударных волн в газах, возникновение подъемной силы крыла, обтекание хорошо обтекаемых тел и многое другое.

Согласно определению идеальной жидкости имеем

pnn = p1 = p2 = p3 = − p .

(4.1)

Положительная скалярная величина p называется давлением*. Знак «ми- нус» перед p указывает, что в жидкости допускаются только сжимающие

нормальные напряжения. Напряжения в идеальной жидкости имеют вид:
в векторной форме	=	−
				(4.2)
pnn			pn ,

* Обычно молчаливо предполагается, что введенная таким образом величина p тождественна давлению, используемому в термодинамике. Однако это обстоятельство нуждается в дополнительном обосновании.

Контакты | https://new.guap.ru/i03/contacts

= − ei

СПБГУАП| Институт 4 группа 4736

64					ГЛАВА IV
в тензорной форме		=	−	pδ ij ,
	pij	=	−	pδ ij ,	(4.3)
в матричной форме
−	p		0	0
		−
	0	−	p	0	,
	0		0
	0		0	− p

где δ ij – дельта Кронекера. Тензор напряжений в идеальной жидкости час-

то называют шаровым или изотропным, так как соответствующая ему тен- зорная поверхность, как легко видеть, представляет собой сферу, а физиче- ские свойства, задаваемые подобными тензорами, изотропны.

В уравнения (2.83) входят величины ∂ ∂ , ∂ ( ) ∂ . На основа- pi xi piv xi

нии равенств (4.1) и (4.3) имеем

			∂ pi	=		∂ ei p


∂ ( piv)	= −		∂ xi			∂ xi	( pvk )
∂ ( piv)	= −	∂ (ei pekvk )			= − ∂		( pvk )


∂ xi		∂ xi					∂ xk

	∂ p	= − p ,		(4.4)
		= − p ,		(4.4)
	∂ xi
= − div pv =			− p div v −	v p . (4.5)

Подставив соотношения (4.4), (4.5) в уравнения (2.83), получаем мо- дель идеальной жидкости

dρ +

div v =

0 ,

ρ F −

p ,

(4.6)

= ρ Fv −

div

+ ρ qe ,

u +

где первое уравнение – уравнение неразрывности, второе – уравнение движения Эйлера, а третье представляет собой закон сохранения энергии.

Система (4.6) содержит пять скалярных уравнений и шесть неизвест- ных (ρ , vi, p, u) . Для ее замыкания необходимо задать уравнение состояния

p = p (ρ ,T) ,

(4.7)

связывающее между собой давление, температуру и плотность, и калори- ческое уравнение состояния

u = u (ρ ,T) .

(4.8)

Система (4.6), (4.7) и (4.8) содержит семь уравнений и семь неизвест- ных и представляет собой замкнутую систему уравнений, описывающих движения идеальной сжимаемой жидкости (газа).

Контакты | https://new.guap.ru/i03/contacts

<<< < Предыдущая 12 / 462 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
10.01.20214.54 Mб82Гидродинамические исследования скважин Курс лекций.pdf
#
10.01.2021459.11 Кб19ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН НА ПРИОБСКОМ МЕСТОРОЖДЕНИИ.pdf
#
07.02.20211.03 Mб21ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН-1.pdf
#
10.01.2021353.18 Кб33Гидродинамические методы исследования скважин.pdf
#
02.01.202138.63 Mб20Гидродинамическое исследование скважин.pdf
#
02.01.202120.67 Mб24гидромеханика нефти.pdf
#
07.02.20211.34 Mб28Гидроочистка сырья.pdf
#
03.02.20211.46 Mб6гидроочистки сырья.pdf
#
24.01.2021452.97 Кб12Гидроразрыв пласта при КРС.pdf
#
24.01.2021271.57 Кб10Гидроразрыв пласта.pdf
#
29.01.2021304.86 Кб7Глубину превращения при термическом крекинге.pdf