гидромеханика нефти

Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

ординатой y +

, будет перенесена

через площадку dσ , нормальную

к оси Ox1 в точку В с координатой y −

.pdf

Скачиваний:

Добавлен:

02.01.2021

Размер:

20.67 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 4615 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

СПБГУАП| Институт 4 группа 4736

ТЕЧЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ ПО ТРУБАМ

185

§5. Течение между двумя вращающимися цилиндрами

Рассмотрим установившееся течение вяз- кой несжимаемой жидкости между двумя неограниченными в направлении вертикаль- ной оси Oz круговыми соосными цилиндра- ми.

Пусть внутренний цилиндр имеет радиус R2 и вращается с угловой скоростью ω 2 , а

внешний имеет радиус R1 и вращается с уг-

ловой скоростью ω 1 (рис. 9.6). Граничные ус-

Рис. 9.6

ловия, очевидно, имеют вид:

при r =

R1 vϕ

= R1ω 1 при r =

vϕ

= R2ω 2 .

(9.55)

Подставив граничные условия (9.55) в равенство (9.53), получаем

C1 = 2

R12ω 1 − R22ω 2

C2 =

R12 R22 (ω 2 − ω 1)

R12 − R22

Следовательно, выражение (9.53) для скорости vϕ имеет вид

R12ω 1 − Rω22

R12 R22 (ω 2 −ω

1)=

( R12 − R22 )

(

R12 − R22

(9.56)

2−ω

R1 ω 1 −

Rω2 2 )

R2ω (

( R12 −

R22 )

Подставив равенство (9.56) в формулу (9.54), после элементарных вы- числений получаем

				p =	ρ	×
					(R12 − R22)2		R14R24 (ω 2 − ω 1)2
× (R12ω	1 − R22ω	2)2	r2	+ 2R12R22 (R12ω 1	− R22ω 2) (ω 2	− ω 1) ln r −		+ C3.
							2r2
		2

При vr =		vz =		0, vϕ = vϕ (r)	тензор скоростей деформаций имеет един-

ственную отличную от нуля компоненту (см. приложение)

ε rϕ =	1	∂ vϕ		−	vϕ	,
ε rϕ =				−		,
	2		∂ r
	2		∂ r		r

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

186

ГЛАВА IX

и в соответствии с формулой (9.23)

напряжение трения τ rϕ

равно

∂

τ rϕ = µ

−

(9.57)

∂ r

Подставив в формулу (9.57) выражение (9.56), получаем

τ r

= − 2µ

R2R2

(ω

−ω

)

(9.58)

( R12

− R22 )

Из формулы (9.58) видно, что с ростом радиуса напряжение трения

убывает как	const	.
убывает как		.
	r2
Сила трения на поверхности цилиндра радиуса r и высотой H равна,
очевидно, 2π rHτ rϕ			, а ее момент относительно оси 0z равен
	M		= 2π r2Hτ r	ϕ	= − 4πµ H	R12R22	(ω		− ω ).	(9.59)
	M		= 2π r2Hτ r		= − 4πµ H	R12 − R22	(ω		− ω ).	(9.59)
						R12 − R22		2	1

Таким образом, момент сил трения не зависит от радиуса цилиндра. Так как при вычислении компонент тензора напряжений нормаль счи-

тается внешней по отношению к рассматриваемому объему, то формулы (9.58) и (9.59) дают значение напряжения и момента сил трения на поверх- ности радиуса r при ее трении о поверхность радиуса r + dr . При рас- смотрении трения поверхности радиуса r о поверхность радиуса r − dr внешняя нормаль имеет направление – r и знак в формулах (9.58) и (9.59) должен быть изменен на противоположный.

Из сказанного следует, что момент сил трения на цилиндрах радиу- сов R1 и R2 будет одинаковым по величине, но противоположным по знаку.

Особый интерес представляет случай, когда внутренний цилиндр по-

коится, то есть ω 2 = 0 . При этом из формулы (9.59) имеем
M =	4πµ		R2R2			ω 1 .
		H		1	2		(9.60)
			R12	−	R22

Формула (9.60) используется для определения вязкости с помощью ротационных вискозиметров с соосными цилиндрами. Действительно, из- мерив угловую скорость ω 1 вращения внешнего цилиндра и момент M на внутреннем цилиндре, с помощью формулы (9.60) можно вычислить ди- намический коэффициент вязкости .

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Глава X

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ

Теория турбулентных течений представляет собой самостоятельный раздел гидромеханики. Исследованию турбулентных течений посвящена весьма обширная литература. Поэтому в настоящей главе рассматриваются лишь наиболее простые и в то же время весьма важные вопросы турбу- лентных течений в трубах.

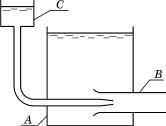
§1. Опыты О. Рейнольдса

	Классические исследования течения
	жидкости в круглых трубах были прове-
	дены в 1876–1883 годах английским фи-
	зиком Осборном Рейнольдсом. Схема его
	экспериментальной установки приведена
	на рис. 10.1. В поток жидкости, выте-
	кающей из большого бака А по длинной
	стеклянной трубе В, через сопло подава-
	лась из бачка С тонкая струйка краски.
	Наблюдения за окрашенной струй-
	кой показали, что при малых скоростях	Рис. 10.1
	течения она вытягивается вдоль оси тру-	Рис. 10.1
	течения она вытягивается вдоль оси тру-

бы, то есть течение происходит без поперечного перемешивания. Слои жидкости движутся параллельно друг другу. Выше указывалось, что такое течение называется ламинарным.

При больших скоростях течения окрашенная струйка размывалась в поперечном направлении по всему сечению трубы, то есть наблюдалось интенсивное перемешивание потока, имевшее ярко выраженный неустано- вившийся характер. Такое течение называется турбулентным. Характерной особенностью турбулентного течения является наличие беспорядочных поперечных составляющих вектора скорости. Таким образом, турбулент- ное течение является по своей сути неустановившимся.

Проведенные эксперименты показали, что переход от ламинарного режима течения к турбулентному определяется не диаметром трубы d ,

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

188			ГЛАВА X
средней скоростью течения w , вязкостью µ			и плотностью ρ , взятыми по
отдельности, а безразмерной комбинацией
Re =	ρ wd	,
Re =		,

получившей название числа Рейнольдса. С точки зрения теории размернос- тей и подобия этот вывод представляется очевидным.

Значение числа Re, при котором происходит переход от ламинар- ного режима течения к турбулентному, называется критическим – Reкр .

При Re < Reкр течение ламинарное, а при Re > Reкр – турбулентное.

Рейнольдс предполагал, что и подтвердилось в дальнейшем, что зна- чение Reкр тем больше, чем меньше возмущение в потоке. Для труб с хо-

рошо закругленным входом при течении воды им были получены значе- ния Reкр порядка 12000–13000. В более поздних исследованиях других ав-

торов в результате ряда мер, принятых с целью уменьшения начальных возмущений, было достигнуто значение Reкр порядка 50000. Однако соз-

дание даже небольших возмущений приводило к немедленной турбулиза- ции таких потоков.

Вто же время различные опыты показали, что при числах Рейнольдса порядка 2200 имеющиеся в потоке (или создаваемые искусственно) воз- мущения затухают, и течение становится ламинарным.

Втехнических устройствах всегда имеются те или иные возмущения. Поэтому при расчете течений в круглых цилиндрических трубах принято считать, что Reкр = 2320.

§2. Осреднение характеристик турбулентного течения

	При измерениях в какой-либо точ-
	ке турбулентного потока безинерцион-
	ным датчиком получается зависимость
	скорости от времени, представленная на
	рис. 10.2, где vx , vy , vz – составляющие
	вектора скорости. Из этих данных видно,
	что величина скорости хаотично пульси-
	рует около некоторого среднего значе-
	ния.
	Рейнольдсом было предложено
Рис. 10.2	рассматривать мгновенное значение ско-

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ

189

рости и всех остальных характеристик турбулентного потока в виде суммы осредненных во времени значений и пульсационных состав- ляющих.

Пусть ϕ (x, y, z, t) – какая-либо характеристика турбулентного потока (скорость, давление и т.д.). Тогда ее мгновенное значение записывается в ви-

де
			ϕ	= ϕ			+ ϕ ′ ,		(10.1)
где ϕ	– значение, осредненное во времени, ϕ ′ – пульсация.
Осредненное значение ϕ			вычисляется как
						t +		T
						2
	ϕ	(x, y, z, t) =			1		∫ϕ (x, y, z,τ ) dτ ,		(10.2)
	ϕ	(x, y, z, t) =			T		∫ϕ (x, y, z,τ ) dτ ,		(10.2)

t − T

где период осреднения Т много больше характерного периода пульсаций, но много меньше характерного времени процесса.

Если величина ϕ , вычисленная для раз- личных значений t , имеет одинаковое значе- ние, то турбулентное течение называется квазистационарным (или стационарным). Ес- ли ϕ зависит от времени (рис. 10.3), то про-

цесс нестационарный.

В случае стационарного течения при

повторном

осреднении параметра ϕ

на

основании формулы (10.2) имеем

t +

Рис. 10.3

(x, y, z) dτ = ϕ

∫ϕ

. (10.3)

t −

Для нестационарных процессов соотношение (10.3) постулируется.

Из формулы (10.2) непосредственно следует, что

= ϕ

ϕ + ψ

+ ψ

(10.4)

В соответствии с формулами (10.1), (10.3) и (10.4) имеем

′ = ϕ

′, ϕ

′ = 0 ,

+ ϕ ′

(10.5)

= ϕ

+ ϕ

то есть осредненное значение пульсации равно нулю.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

190 ГЛАВА X

В случае квазистационарного течения, как это следует из определения осреднения (10.2),

	t+ T
	2
ϕ ψ =	T1 ∫ϕ (x, y, z) ψ ( x, y, z,τ) dτ = ϕ ψ .	(10.6)

t− T

Для нестационарных процессов соотношение (10.6) постулируется.

Из формул (10.5) и (10.6) следует, что

= ϕ

′ =

ψ ′

0 .

(10.7)

В соответствии с правилом дифференцирования интеграла с перемен-

ными пределами имеем

∂ ϕ

1 ∂

ϕ (x,y, z,τ ) dτ =

ϕ x,y, z,t +

−

ϕ x,y, z,t −

∂ t T ∂ t ∫

t−

(10.8)

∂ ϕ

∫

dτ =

∂ t

∂ τ

t− T

то есть производная по времени осредненного значения равна осредненно- му значению производной.

Равенство
	∂ ϕ
	∂ ϕ	=		∂ ϕ	(10.9)
	∂ xi	=	∂ xi		(10.9)
	∂ xi		∂ xi

очевидно.

§3. Уравнение Рейнольдса

Уравнения Рейнольдса представляют собой уравнения движения вяз- кой несжимаемой жидкости, записанные для осредненных параметров по- тока.

Рассмотрим уравнения движения вязкой несжимаемой жидкости (4.42),

или

∂ vi	= 0,	ρ	dvi	= ρ Fi −	∂ p	+ µ ∆ vi .	(10.10)

∂ xi			dt		∂ xi

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ

191

Положим в соответствии с гипотезой Рейнольдса, что

p =

p′, vi

vi′ .

(10.11)

vi +

Для удобства дальнейших преобразований заметим, что в случае не-

сжимаемой жидкости можно записать

dvi

+ vi

∂ vj

dvi

∂ vi

+ vj

∂ vi

+ vi

∂ vj

∂ vi

∂ (vivj )

. (10.12)

∂ xj

∂ t

∂ xj

∂ t

∂ xj

Подставив в равенство (10.12) соотношение (10.11) для скорости, на осно- вании правил осреднения (10.3)–(10.9) с учетом уравнения неразрывности получим

∂ (

vj )

∂

vi′v′j

dvi

(10.13)

∂

∂ xj

∂

Далее очевидно, что на основании правил осреднения

∂

∂ vi

∂ p

∆ vi

∆

(10.14)

vi ,

∂ xj

∂ xi

Из равенств (10.13), (10.14) и уравнений (10.10) имеем окончательно

∂ (

)

∂

vi′v′j

= 0,

ρ Fi

−

µ ∆ vi

−

(10.15)

∂ xi

∂ xj

или в векторном виде

∂ (

)

v′v′j

−

div

= ρ F

µ ∆

−

(10.16)

∂ xj

Таким образом, в результате проведенного осреднения уравнение не- разрывности сохранило свой вид, а в уравнениях движения появились до- полнительные члены вида ρ vi′v′j .

Для понимания полученного результата воспользуемся уравнениями движения сплошной среды в напряжениях (2.49)

ρ		dv	=	ρ F +	∂ pi		(10.17)


		dt			∂ xi
или
ρ	dvj		=	ρ Fj +	∂ pij	.	(10.18)
ρ			=	ρ Fj +		.	(10.18)
	dt				∂ xi

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

192

ГЛАВА X

Осредняя уравнения (10.17) и (10.18) по времени, с учетом равенства (10.13) получим

ρ F +

∂

(pi

−

ρ v′vi′) ,

(10.19)

∂ xi

∂

(

) .

dvj

−

v′v′

(10.20)

∂ xi

j i

Уравнения (10.15), (10.16), (10.19), (10.20) представляют собой раз-

личные формы записи уравнений Рейнольдса.

Из уравнений Рейнольдса следует, что при временном осреднении тур- булентного течения дополнительно к тензору осредненных вязких напряже- ний

pji = − pδ ji + 2µ ε ji

возникает симметричный тензор турбулентных напряжений


	−	ρ v1′v1′

	−	ρ	v′v′
			2 1
			v′v′
−		ρ
			3 1

−ρ v1′v2′

−ρ v2′v2′

−ρ v3′v2′


−	ρ	v′v′
		1	3
−	ρ	2	3		(10.21)
		v′v′		.

−	ρ	v′v′
		3	3

Таким образом, уравнения Рейнольдса содержат 6 дополнительных неизвестных – компонент тензора турбулентных напряжений (10.21) и, следовательно, являются незамкнутыми. Вопрос об их замыкании, то есть вопрос об отыскании связи между тензором турбулентных напряже- ний и осредненными характеристиками потока, представляет собой до на- стоящего времени одну из основных проблем теории турбулентности.

§4. Полуэмпирическая теория турбулентности Л.Прандтля

Полуэмпирические теории турбулентности основываются на каких-либо гипотезах, связывающих турбулентные напряжения с полем осредненных скоростей. Основой для формулирования этих гипотез является обобщение экспериментального материала и введение в получающиеся таким образом соотношения эмпирических констант.

При построении полуэмпирических теорий используется изложенная выше идея О.Рейнольдса о представлении поля скоростей турбулентного

потока в виде суммы поля осредненных скоростей v и поля пульсацион- ных составляющих v′. При этом вводятся линии тока осредненного дви- жения, непроницаемые для осредненных скоростей, но проницаемые для

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ

193

пульсационных составляющих, благодаря которым происходит поперечное перемешивание в турбулентном потоке.

Пульсационные составляющие скорости переносят сквозь линии тока осредненного течения некоторое количество движения, что приводит в соот- ветствии со вторым законом Ньютона к возникновению дополнительных – турбулентных – напряжений.

Рассмотрим плоское квазистационарное турбулентное течение между

неподвижными плоскостями y = 0 и y = h (рис. 10.4).		Очевидно, что
в этом случае		vz′ = 0 – по оп-
	vy = 0 из-за непроницаемости стенок, а vz =

ределению плоского течения. Линии тока осредненного течения – прямые, параллельные оси Ox . Ясно, что отличными от нуля компонентами тензо-

ра турбулентных напряжений будут

−

x x

−

y y

− ρ

x y

= − ρ

y x

v′ v′

v′v′ ,

v′ v′

v′v′ .

Как показывают эксперименты, величинами

можно пре-

x x

y y

v′ v′ и

v′v′

небречь.

Рис. 10.4

Введем обозначения

, v′

v′,

− ρ

v′

= τ

и будем считать, что трение приложено от верхнего слоя к нижнему, то есть будем рассматривать нижний слой жидкости (рис. 10.4). При этом, очевидно, перенос количества движения сверху вниз необходимо учиты- вать со знаком «+», а снизу вверх – со знаком «–». Из-за наличия пульса- ционной составляющей v′ частица жидкости, находящаяся в точке А с ко-

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

194

ГЛАВА X

точке

l′

рассматриваемая

частица имела

осредненную

ско-

рость u =

u y +

. В соответствии с гипотезой Л.Прандтля

, скорость

частицы

на

пути

l′ не меняется,

а в точке В

становится равной

l′

u =

u y −

. Так как поток массы через площадку dσ равен ρ v′ dσ

, то

изменение осредненного по времени количества движения нижнего слоя равно**


	l′			l′
ρ v′ u y +		−	u y −		dσ .
ρ v′ u y +		−	u y −		dσ .
	2			2

Следовательно, осредненная во времени сила турбулентного трения τ dσ

равна

τdσ =
τdσ =	ρ v′ u y +

l′			l′
	−	u y −		dσ .	(10.22)

2			2

Величина l′ называется длиной пути перемешивания.

Так как величина l′ предполагается малой, то с точностью до членов

более высокого порядка малости

l′

l′ du

u(y) ±

(10.23)

u y

2 dy

Подставив разложение (10.23) в равенство (10.22), получим

τ =

= A

v′l′

(10.24)

где A = ρ v′l′ – динамический коэффициент турбулентной вязкости. Выражение для дополнительного турбулентного напряжения в ви-

де τ = A du было предложено, по аналогии с законом трения Ньютона dy

для ламинарного течения, французским ученым Ж.Буссинеском*** в 1887 г. Однако необходимо особо подчеркнуть, что коэффициент турбулентной вяз- кости А, в отличие от динамического коэффициента вязкости , не есть константа, характеризующая жидкость, а зависит от координаты y и пара- метров потока.

*Людвиг Прандтль (1875–1953), немецкий ученый, один из основателей аэромеханики.

**В соответствии с законом сохранения массы переход частицы из точки А в точку В сопровождается переходом другой частицы из В в А.

***Жозеф Валантен Буссинеск (1842–1929), французский ученый в области механики.

Контакты | https://new.guap.ru/i03/contacts

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 4615 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
10.01.20214.54 Mб82Гидродинамические исследования скважин Курс лекций.pdf
#
10.01.2021459.11 Кб19ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН НА ПРИОБСКОМ МЕСТОРОЖДЕНИИ.pdf
#
07.02.20211.03 Mб21ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СКВАЖИН-1.pdf
#
10.01.2021353.18 Кб33Гидродинамические методы исследования скважин.pdf
#
02.01.202138.63 Mб20Гидродинамическое исследование скважин.pdf
#
02.01.202120.67 Mб24гидромеханика нефти.pdf
#
07.02.20211.34 Mб28Гидроочистка сырья.pdf
#
03.02.20211.46 Mб6гидроочистки сырья.pdf
#
24.01.2021452.97 Кб12Гидроразрыв пласта при КРС.pdf
#
24.01.2021271.57 Кб10Гидроразрыв пласта.pdf
#
29.01.2021304.86 Кб7Глубину превращения при термическом крекинге.pdf