2.4. Другие формы импульсов тока и их гармонический анализ

Рассмотрим два примера расчета гармоник импульсов сложной формы. Если нужно учесть кривизну начального участка любой характеристики АЭ (см. рис. 2.1), то удобно аппроксимировать зави­симость i(e_BX) параболой с отсечкой:

(2.28)

Здесь α— коэффициент, определяемый по реальной характеристике. С учетом (2.6) и (2.9)

(2.29)

Гармоники такого импульса можно представить в форме, подоб­ной (2.21):

γ _n(Θ, 2), n=1,2,… (2.30)

Второй аргумент коэффициентов разложения γ_n(Θ, 2) соответ­ствует степени параболы (2.28). Подробные таблицы коэффициентов γ_и(Θ, 2) содержатся в [6]. Аналогично выполняется гармонический анализ при аппроксимации i(e_BX) параболой любой степени с отсеч­кой [6].

Другой пример импульса тока сложной формы встречался при изучении ПР. Импульс, показанный на временной диаграмме рис. 2.5, в, является алгебраической суммой косинусоидальных импульсов, показанных на рис. 2.10. Из импульса (2.18) с углом отсечки Θ (рис. 2.10, б) вычитаются: 1) импульс с такой же амплиту­дой образующей его косинусоиды, но с углом отсечки Θ₁ (2.16) (рис. 2.10, в); 2) импульс, характеризуемый амплитудой S_кpU_н и углом отсечки Θ₁ (рис. 2.10, г).

Гармонические составляющие выходного тока в ПР рассчитыва­ются по формуле;

= [γ_n(Θ) -γ_n(Θ)]-S_кр U_нγ_n (Θ₁) (2.31)

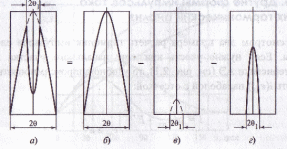
Рис. 2.10. Импульс выходного тока АЭ в перенапряженном режиме (а) и его составляющие (б—г)

Изложенные в этом параграфе подходы позволяют получить ана­литические выражения для амплитуд гармонических составляющих симметричных импульсов достаточно сложной формы.

2.5. Нелинейная модель биполярного транзистора и аппроксимация ее характеристик

При изучении инерционных АЭ недостаточно использовать стати­ческие характеристики. Связь между токами и напряжениями в этом случае определяется системой нелинейных дифференциальных урав­нений.

Примером инерционных АЭ являются биполярные транзисторы. Процессы в них в значительной части диапазона рабочих частот удовлетворительно описываются нелинейной зарядовой моделью (рис. 2.11), отражающей связь токов коллектораi_к и базы i_б с избы-

Рис. 2.11. Нелинейная зарядовая модель биполярного транзистора (теоретиче­ская модель обведена штрихпунктирной линией)

точным зарядом q неосновных носителей в базе и зарядом барьерных емкостей эмиттерного С_э и коллекторного С_к переходов.

Емкость С_к принято разделять на две составляющие:

С_к = С_к.а. + С_к.п (2.32)

где С_ка — емкость активной части, расположенной непосред­ственно под эмиттером; С_кп — емкость оставшейся, пассивной части перехода.

В соответствии со схемой рис. 2.11 запишем выражения для токов внутренней части (теоретической модели) биполярного транзистора (без учета r₆, С_э, С_к):

(2.33)

Здесь i _к.г — ток коллекторного генератора тока, управляемого избы­точным зарядом в базе; i_б.т — ток базы теоретической

модели; τ_т — среднее время пролета носителей через базу; τ_β — среднее время жизни неосновных носителей в базе, определяющее рекомбинационную составляющую тока базы i_{б рек} = q/τ_β

Величину τ_т можно оценить по приводимой в справочниках гра­ничной частоте τ_т а τ_β τ_т. Последнее соотношение вытекает непосредственно из (2.33), поскольку статический коэффи­циент передачи тока базы

Полные выражения для токов имеют вид:

(2.34)

где е_п — напряжение на эмиттерном переходе; i_с._к — ток смещения через суммарную емкость С_к ,

(2.35)

Для расчета токов транзистора в нелинейном режиме на умеренно высоких частотах, как правило, используется метод заряда [1—3]. При этом принимается, что накопленный в базе заряд q и составляю­щая тока коллектора i_к.г = q/τ_т безынерционно связаны с напряже­нием на эмиттерном переходе:

, (2.36)

где = τ_т , а — обратный тепловой ток коллектора; — температурный

потенциал ( 25...33 мВ при Т =

290...400 К). Фактически накопленный заряд q и ток г_к.г запазды­вают на время (0,2—0,4)τ_т относительно изменения напряжения на переходе е_п. Этим запаздыванием можно пренебрегать, если рабочая частота не превышает граничной частоты коэффициента усиления транзистора по току в схеме с общим эмиттером: ω< ω_гр и 1/τ_т, где рассматриваемая модель применима.

Дополним (2.33)—(2.36) дифференциальным уравнением для напряжения на переходе. Для этого в соответствии со схемой рис. 2.11 запишем составляющую тока базы, протекающую через эмиттерный переход, i_б._п = i_б._т + С_э de _п /dt как сумму токов через

сопротивление базы и емкость С_{к а}:

Подставив в это уравнение i_б._т из (2.33), получим

(2.37)

Система уравнений (2.33)—(2.37) описывает процессы в транзис­торе, работающем в активной области и области отсечки. Для инже­нерных расчетов усилителей мощности и умножителей частоты малой кратности нелинейную зависимость (2.36) в области рабочих значений накопленного заряда можно заменить кусочно-линейной:

(2.38)

где С_диф — средняя для активной области диффузионная емкость; Е' — напряжение отсечки (индекс «о» показывает, что транзистор открыт).

Подставив (2.38) в (2.33), получим аппроксимированные характе­ристики токов теоретической модели:

; (2.39)

(2.40)

где S_n = С_диф/τ_т — усредненная крутизна коллекторного тока по напряжению на переходе: 1 / r_б — усредненная крутизна рекомбинационной составляющей базового тока, причем 11 r_б = С_диф / τ_β = S_n /h _21э.

Дифференциальные параметры зарядовой модели

и пропорциональны крутизне коллекторного тока S_n = di_к.г/ ei_п и, следовательно, согласно (2.36) при i_к.г >> I_к.о.т линейно зависят от тока коллектора:

(2.41)

В связи с этим для повышения точности расчетов при применении кусочно-линейной аппроксимации характеристик транзистора (2.38)—(2.40) необходимо учитывать высоту импульса коллектор­ного тока i_к.м. Рекомендуется брать усредненные параметры С_диф, S_n и 1/ τ_β равными их дифференциальным значениям при токе i_к.г = 0,5i_к.м и проводить прямую, аппроксимирующую вольт-амперную характеристику i_к.г(е_п), через точку, соответствующую току i_к.м

Согласно (2.41) крутизна обратно пропорциональна ,

т.е. абсолютной температуре коллекторного перехода Т. При полном использовании транзистора по мощности температура перехода близка к максимально допустимой (t = 120... 150 °С). В этом случае мВ и можно приближенно принять

В статическом режиме ток коллектора i_к равен току генератора i_к.г,

а напряжение е_б.э = е_п + i_бr_б.

Из этого равенства и из (2.39), (2.40) следует, что аппроксимиро­ванные характеристики определяются соотношениями:

(2.42)

(2.43)

где S = K_nS_п; S_б = К_п/r_β; К_п — средний для активной области коэф­фициент деления напряжения во входной цепи транзистора на низ­ких частотах,

(2.44)

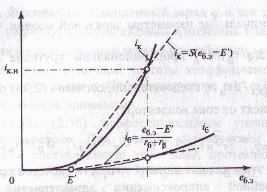
Рис. 2.12. Статические характеристики i_K, i_б(е_б.э)> соответствующие зарядовой модели, и их аппроксимация

Рис. 2.13. Кусочно-линейная высокочастотная модель биполярного транзистора для областей активной и отсечки

Пример аппроксимации статических характеристик i_б(е_б.э) и i_к(е_б.э) показан на рис. 2.12.

Принятой полигональной аппроксимации соответствует кусочно-линейная высокочастотная модель биполярного транзистора (рис. 2.13). Для упрощения анализа нелинейные емкости С_к.а, С_к.п и С_э здесь также заменены постоянными, равными средним для рабо­чих интервалов напряжений значениям. При замкнутом положении ключа К транзистор находится в активной области, при разомкну­том — в области отсечки. Переход из одной области в другую проис­ходит в тот момент, когда напряжение на переходе е_п проходит через

напряжение отсечки .