7.3.3. Анализ устойчивости стационарных режимов в автогенераторах с автосмещением. Режимы прерывистой генерации и самомодуляции

Возможность реализации стационарного режима, которому в плоскости диаграмм срыва и смещения соответствует точка равнове­сия, лежащая на участке диаграммы срыва с отрицательным угловым

коэффициентом (см. рис. 7.12), еще не означает, что этот режим

будет устойчив. При постоянном напряжении смещения режим, кото­рому соответствует точка с такими координатами, был бы неустой­чив. Сколь угодно малое увеличение амплитуды U_BX при фиксирован­ном Е_с привело бы к сдвигу точки внутрь диаграммы срыва, т. е. в область, лежащую правее этой диаграммы.

В этой области мощность, отдаваемая АЭ, превышает мощность, рассеиваемую в колебатель­ной системе, поэтому амплитуда U_BX продолжала бы нарастать до стационарного значения, лежащего в перенапряженном режиме. При отклонении U_BX вниз от стационарного значения при Е_с = const изоб­ражающая точка попадает в область, лежащую вне диаграммы срыва, где мощность потерь превышает поступающую мощность, поэтому амплитуда U_BX уменьшается до нуля.

Но в АГ с автосмещением напряжение Е_с не остается постоян­ным. При анализе устойчивости точки равновесия, показанной на рис. 7.12, рассмотрим сначала случай, когда емкости цепи автосме­щения С_вх0 и С_э0 на схеме рис. 7.8 выбраны настолько малыми, что при отклонении от состояния равновесия скорость изменения напря­жения смещения Е_с гораздо больше скорости изменения амплитуды колебаний, которая в первом приближении определяется постоянной времени колебательного контура, задающего частоту колебаний.

Тогда при малом отклонении U_BX и Е_с от их стационарных значений сначала за короткое время установится значение напряжения смеще­ния, соответствующее новому значению амплитуды, и лишь затем будет происходить изменение амплитуды, за которым будет следо­вать изменение смещения. Таким образом, вторая фаза движения будет происходить практически по диаграмме смещения. Будем называть такое автосмещение безынерционным.

Рассмотрим переходные процессы в АГ с безынерционным авто­смещением при отклонениях U_BX и Е_с от их стационарных значений. На рис. 7.13 показаны диаграмма срыва, соответствующая SZ_y « 3, и диаграмма смещения с G_c = 20, взятые из рис. 7.12.

Обозначим координаты стационарной точки Е_с0 и U_Bx0, пусть возмущение вызывает увеличение амплитуды до U_BX1 > U_{BX 0} при _Ec1 = Е_с0 = 0.

Соответствующая точка а показана на рис. 7.13. При без­ынерционном автосмещении первая фаза движения из точки (Е_с1 у U_BX1)

будет представлять собой быстрое изменение Е_с от значения Е'_с1 =

= E_c0 = 0 до значения Е'_c1, лежащего на диаграмме смещения и соот-

ветствующего значению U_BX1,, которое в течение первой фазы движе­ния остается практически неизменным (точка а^’). При этом изобра­жающая точка а' (Е, U_вх1) окажется вне диаграммы срыва, где мощность, доставляемая АЭ, меньше мощности, рассеиваемой в колебательной системе, поэтому амплитуда будет уменьшаться так, что изображающая точка будет двигаться по диаграмме смещения. Такое движение вернет ее в точку стационарного режима. Состояние равновесия после такого возмущения восстановится. Если подей­ствует возмущение, которое уменьшит амплитуду до значения U_Bx2^< < U_BX0 при Е_{с 2} = Е_с о = 0 (точка б на рис. 7.13), то на первой фазе движения, вызванного этим возмущением, изображающая точка быс­тро переместится на диаграмму смещения, т.е. в точку б' с координа­тами (Е'₂, U_bx2). Эта точка лежит внутри диаграммы срыва, где амплитуда колебаний U_Вx должна расти. Но ее рост будет происхо­дить при одновременном изменении Е_с, обеспечивающем движение изображающей точки к состоянию равновесия (см. рис. 7.13). Таким образом, и после этого возмущения состояние равновесия восстано­вится. Аналогичным образом можно рассмотреть изменение Е_с и U_BX при любом возмущении (например, из точки в на рис. 7.13) и пока-

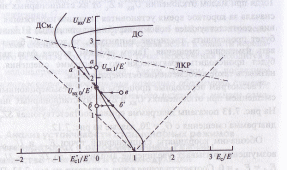
Рис. 7.13. К пояснению процессов изменения напряжения смещения и ампли­туды колебаний в автогенераторе с безынерционным автосмещением при отклонениях от точки стационарного режима, лежащей на участке диаграммы срыва с отрицательным угловым коэффициентом

зать, что точка стационарного режима (Е_{с 0}, U_{BX 0}) при безынерцион­ном автосмещении устойчива.

Приведенные рассуждения доказывают, что при использовании безынерционного автосмещения стационарные колебания в АГ с запасом по самовозбуждению больше двух при работе АЭ в недона­пряженном режиме будут устойчивы. Точнее говоря, характерные постоянные времени цепей автосмещения, показанных на схеме рис. 7.8, U_вх о = R_{BX 0} С_{ВХ 0} и

Т_э0=R_э0С_Э0 должны быть много меньше постоянной времени Т_к колебательного контура АГ, определяющего частоту автоколебании <в₀. Значение Т_к рассчитывается по формуле Т_к ⁼ 2Q/ω₀, где Q — добротность нагруженного контура.

С учетом изложенного здесь подхода рассмотрим вопрос об устойчивости той же точки стационарного режима для очень инерци­онных цепей автосмещения, когда Т_{вх 0}>>Т_к и Т_э0 >> Т_к. В этом слу­чае при отклонении точки (Е_с, U_BX), характеризующей состояние АГ, от точки равновесия процессы изменения амплитуды колебаний, вызванные нарушением энергетического баланса в точке равновесия, будут происходить значительно быстрее, чем процессы установления напряжения смещения Е_с, соответствующего этой амплитуде. Про­цессы изменения амплитуды колебаний U_BX и напряжения смещения Е_с при очень инерционном автосмещении поясняются рис. 7.14.

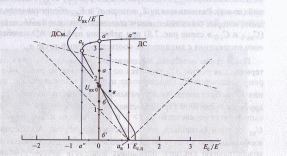
Рис. 7.14. К пояснению процессов изменения напряжения смещения и ампли­туды колебаний в автогенераторе с очень инерционным автосмещением при отклонениях от точки стационарного режима, лежащей на участке диаграммы срыва с отрицательным угловым коэффициентом

При отклонении точки, характеризующей состояние АГ в плос­кости

(Е_с, U_BX), от точки равновесия вверх (в точку а на рис. 7.14) мощность, поступающая в колебательную систему, превышает рассе­иваемую и амплитуда автоколебаний будет расти. При очень инерци­онном автосмещении изображающая точка достигнет диаграммы срыва, на которой обе мощности равны, настолько быстро, что напряжение Е_с почти не изменится.

Этой ситуации соответствует движение по вертикальной линии а—а' до диаграммы срыва. Однако напряжение Е_с в точке а' превышает равновесное, значение которого определяется координатой Е_с на диаграмме смещения, соответствую­щей значению U_BX в точке а', поэтому напряжение Е_с будет умень­шаться. При этом изображающая точка будет медленно двигаться по диаграмме срыва до точки а_с, в которой касательная к диаграмме срыва вертикальна. При дальнейшем уменьшении Е_с изображающая точка попадает в область, лежащую левее диаграммы срыва.

В этой области рассеиваемая в колебательной системе мощность превышает доставляемую АЭ и колебания будут убывать. При очень инерционном автосмещении время уменьшения амплитуды U_вх до нулевого значения настолько мало, что напряжение Е_с практически не изменится, и переход из точки срыва а' в точку а", где амплитуда колебания становится равной нулю, происходит почти по вертикаль­ной линии. Поэтому в точке а" напряжение смещения гораздо меньше значения Е_с._п, соответствующего режиму отсутствия колеба­ний (покоя). Разница между Е_с в точке а" и Е_с „ обеспечивается заря­дами, которые были накоплены в конденсаторах цепей автосмещения (С_вх0 и С_э0 в схеме рис. 7.8) при действии на входе АЭ колебатель­ного напряжения с амплитудой, соответствующей точке а_с.

После срыва колебаний конденсаторы разряжаются и точка, харак­теризующая режим АГ, движется по оси абсцисс на рис. 7.14 в сто­рону увеличения Е_с. Однако после перехода напряжением Е_с значе­ния Е' изображающая точка оказывается в области значений Е_с, где крутизна проходной характеристики становится равной S. При этом выполняется неравенство SZ_y > 1 и сколь угодно малое отклонение С/_вх от нуля (например, из-за собственных шумов АЭ) переводит изображающую точку в область, где мощность, доставляемая АЭ в колебательную систему, превышает мощность потерь.

Амплитуда автоколебаний начинает расти и за время порядка нескольких Т_к достигает значения U_BX, соответствующего координате точки а'", лежащей на диаграмме срыва. За время перехода изображающей

точки от а_в до а'" напряжение Е_с изменяется незначительно и линию перехода на рис. 7.14 можно считать вертикальной. Возникновение колебаний с такой амплитудой приводит к росту отрицательных напряжений на емкостях С_вх0 и С_э0 и движению изображающей точки по диаграмме срыва от а'" к а_с.

Таким образом, в схеме с очень инерционным автосмещением стационарный режим, соответствующий точке, расположенной на участке диаграммы срыва с отрицательным наклоном, неустойчив. Вместо него возникает режим генерации периодической последова­тельности радиоимпульсов, сопровождаемой периодическим измене­нием напряжения смещения. Его называют режимом прерывистой генерации, и для подавляющего большинства АГ такой режим не является рабочим.

В реальных схемах АГ при заданном значении Т_к одновременное увеличение постоянных времени Т_с.вх = R_вх0С_вх0 и Т_сэ = R_э0С_э0 приводит сначала к переходу от неколебательных процессов установ­ления стационарных значении U_BX и Е_с, соответствующих рис. 7.13, к процессам колебательного установления значений U_BX и Е_с. Затуха­ние этих процессов по мере увеличения Т_{с вх} и Т_{с э} становится все более медленным. После перехода некоторых граничных значений T_с.вх.гр и T_с.э.гр стационарного режима теряет устойчивость и возникает режим самомодуляции амплитуды колебаний. Дальнейшее увеличение Т_с.вх и Т_с.э приводит к переходу от режима самомодуля­ции к режиму прерывистой генерации. Примеры осциллограмм коле­баний в АГ в режимах самомодуляции и прерывистой генерации показаны на рис. 7.15.

Рис. 7.15. Осциллограммы колебания в автогенераторе при работе в режимах самомодуляции (а) и прерывистой генерации (б)

Точные соотношения между Т_к, с одной стороны, и Т_свх, Т_сз, с другой, на границе устойчивости стационарного режима находятся при анализе АГ с использованием дифференциальных уравнений для амплитуды автоколебаний и напряжения смещения [5, 19]. Для оце­ночных расчетов при Т_{с вх} ≈ Т_сэ условие устойчивости можно запи­сать в виде

Т_с.вх + Т_с.э < Т_к. (7.56)

Опираясь на эту оценку, можно судить о степени сложности задачи обеспечения устойчивости режимов, рассмотренных в данном пункте.