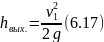- •Гидравлика
- •Сведения из истории гидравлики в пгупс.
- •1 Введение в гидравлику
- •1.1 Определение науки «Гидравлика».
- •1.2 Жидкость.
- •1.3. Понятия реальной и идеальной жидкости. Вязкость.
- •1.4. Основные физические свойства реальных жидкостей.
- •1.4.1. Плотность жидкости ρ, вес единицы объёма γ.
- •1.4.2. Сжимаемость жидкости.
- •1.4.3. Расширение жидкости в связи с изменением температуры.
- •1.4.4. Сопротивление жидкости растягивающим усилиям.
- •1.5. Силы, действующие на жидкость. Напряженное состояние жидкости.
- •Гидростатика.
- •1.6. Гидростатическое давление и его свойства.
- •1.7. Дифференциальные уравнения покоя жидкости.
- •1.8 Интегрирование дифференциальных уравнений покоя (равновесия) жидкости.
- •1.9 Величина гидростатического давления в случае жидкости, находящейся под действием только одной объёмной силы – силы тяжести.
- •1.10 Вакуум
- •1.11 Статика газов
- •1.11.1 Уравнения состояния газов
- •1.11.2 Распределение давления газа по высоте
- •1.11.3 Распределение температуры газа по высоте
- •1.12 Относительный покой жидкости.
- •1.12.1 Свободная поверхность жидкости при равноускоренном или равнозамедленном прямолинейном движении.
- •1.12.2 Определение величины гидростатического давления.
- •1.13 Сила гидростатического давления, действующая на плоскую фигуру любой формы.
- •1.13.1 Сила pа
- •1.13.2. Положение центра давления.
- •1.14 Сила гидростатического давления, действующая на плоские прямоугольные фигуры.
- •1.15 Сила гидростатического давления, действующая на цилиндрические поверхности.
- •1.15.1 Первый случай цилиндрической поверхности.
- •1.15.2 Второй случай цилиндрической поверхности (вертикаль cc’ лежит внутри жидкости).
- •1.15.3 Третий случай цилиндрической поверхности.
- •1.16 Равновесие плавающих тел. Закон Архимеда.
- •1.17 Плавучесть тела и условия её обеспечения.
- •1.18 Остойчивость плавающего тела.
- •2. Основы технической гидродинамики.
- •2.1 Линия тока
- •2.2 Параллельноструйное, плавно изменяющееся и резко изменяющееся движения жидкости. Живое сечение, расход, средняя скорость и эпюра скоростей.
- •2.3 Неравномерное и равномерное, напорное и безнапорное движения жидкости.
- •2.4.1 Случай резко изменяющегося движения жидкости.
- •2.4.2. Случай плавно изменяющегося и параллельноструйного движений жидкости.
- •2.4.3 Уравнение неразрывности для газов
- •2.5 Уравнения Эйлера движения невязкой (идеальной) жидкости.
- •2.6 Интеграл Бернулли.
- •2.7 Уравнение Бернулли для идеальной несжимаемой жидкости.
- •2.8. О распределении давления в живых сечениях потока при параллельноструйном и плавно изменяющемся движениях жидкости.
- •2.9.1 Влияние неравномерности распределения скоростей u по плоскому живому сечению на количество движения (кд) массы м.
- •2.9.2. Влияние неравномерности распределения скоростей u по плоскому живому сечению на кинетическую энергию (кэ) массы м.
- •2.10 Уравнение Бернулли для целого потока реальной (вязкой) жидкости при установившемся движении.
- •2.11 Уравнение Бернулли для газов.
- •2.12 Гидравлическое уравнение количества движения для установившегося движения реальной жидкости.
- •2.13 Два режима движения реальной жидкости.
- •3. Потери напора при установившемся движении жидкости.
- •3.1 Общие указания о потерях напора. Гидравлические сопротивления.
- •3.2 Основное уравнение установившегося равномерного движения жидкости для «правильных» русел. Работа сил внутреннего трения.
- •3.3 Законы внутреннего трения в жидкости. Величина касательных напряжений трения при ламинарном движении жидкости.
- •3.4 Распределение скоростей u по живому сечению при ламинарном равномерном установившемся движении жидкости.
- •3.5 Формула Пуазейля для расхода q в круглоцилиндрической трубе. Потеря напора по длине при ламинарном равномерном установившемся движении жидкости.
- •3.6 Уравнения Навье-Стокса движения вязкой жидкости.
- •3.7 Пример точного решения уравнений Навье-Стокса.
- •4 Уравнения Рейнольдса.
- •4.1 Принципы осреднения актуальных (истинных) движений при турбулентном режиме. Пульсационные добавки.
- •4.2 Уравнения движения при турбулентном режиме потока.
- •5 Потеря напора при установившемся равномерном движении жидкости.
- •5.1 Коэффициент гидравлического трения.
- •5.2 Потери напора по длине при турбулентном установившемся равномерном движении жидкости для квадратичной области сопротивления.
- •6 Местные потери напора при турбулентном напорном установившемся движении жидкости.
- •6.1 Потери напора при резком расширении напорного трубопровода (формула Борда).
- •6.2 Остальные случаи местных потерь напора. Общая формула Вейсбаха.
- •6.3 Гидравлический расчет коротких трубопроводов.
- •6.4 Всасывающая труба насоса.
- •6.5 Гидравлический расчет длинных трубопроводов.
- •6.6 Расчёт трубопроводов для газов.
- •6.6.1 Расчет при малых перепадах давления.
- •6.6.2 Расчёт газопроводов при больших перепадах давления.
- •6.6.3 Гидравлический расчёт вытяжной дымовой трубы.
- •6.7 Понятие о гидравлическом ударе в трубопроводах
- •7 Истечение жидкости из отверстий и насадков.
- •7.1 Истечение из малого отверстия в атмосферу при постоянном напоре.
- •7.2 Траектория струи.
- •6.3 Истечение жидкости из насадков при постоянном напоре.
- •6.3.1 Внешний круглоцилиндрический насадок (насадок Вентури).
- •6.3.2 Внутренний круглоцилиндрический насадок (насадок Борда).
- •7.4 Истечение жидкости из отверстия в атмосферу при переменном напоре.
- •8 Равномерное безнапорное установившееся движение воды в открытых каналах.
- •8.1 Гидравлические элементы живого сечения потока в канале.
- •8.2 Гидравлически наивыгоднейший поперечный профиль трапецеидального канала.
- •8.3 Основные задачи при расчёте трапецеидальных каналов на равномерное движение.
- •8.4 Ограничение скоростей движения воды при расчёте каналов. Перепады.
- •1. Мероприятия по увеличению скорости .
- •2. Мероприятия по уменьшению скорости .
- •8.5 Расчёт каналов, имеющих замкнутый поперечный профиль.
- •1. Канализационные трубы.
- •9 Неравномерное безнапорное установившееся движение воды в каналах и естественных руслах.
- •9.1 Предварительные указания.
- •9.2 Основное дифференциальное уравнение неравномерного движения воды.
- •9.3 Второй вид дифференциального уравнения неравномерного движения воды.
- •9.4 Второй вид дифференциального уравнения неравномерного движения воды для случая цилиндрических русел.
- •9.5 Четыре вспомогательных понятия: удельная энергия сечения, критическая глубина, нормальная глубина, критический уклон.
- •9.6 Спокойное, бурное и критическое состояния потока.
- •9.7. Исследование форм (видов) кривой свободной поверхности потока в случае неравномерного плавно изменяющегося движения воды в цилиндрическом русле.
- •9.8 Построение кривой свободной поверхности потока по уравнению Бернулли методом конечных разностей (способ Чарномского)
- •10 Гидравлический прыжок и послепрыжковый участок.
- •10.1 Общие указания. Послепрыжковый участок.
- •10.2 Основное уравнение гидравлического прыжка.
- •10.3 Прыжковая функция. Определение одной из сопряжённых глубин по заданной другой сопряжённой глубине.
- •10.4 Основное уравнение прыжка в прямоугольном цилиндрическом русле.
- •10.5 Длина свободного прыжка в прямоугольном горизонтальном русле. Потери энергии в прыжке.
- •10.6 Особые виды гидравлического прыжка.
- •11 Водосливы
- •11.1 Терминология и классификация водосливов
- •11.2 Основная расчётная формула для прямоугольного водослива
- •11.3 Свободное истечение через неподтопленный прямоугольный водослив с вертикальной стенкой
- •11.4. Неподтопленный водослив с широким порогом
- •11.5 Критерий подтопления водослива с широким порогом
- •12 Сопряжение бьефов при устройстве плотин
- •12.1 Типы сопряжения бьефов
- •12.2. Гасители энергии потока
- •13. Плавно изменяющееся установившееся безнапорное движение грунтовой воды
- •13.1 Основные понятия
- •13.2 Ламинарная и турбулентная фильтрация
- •Значения коэффициента формы частиц крупнозернистых материалов
- •Величина коэффициента c0
- •13.3 Формула Дарси
- •13.4 Основное уравнение плавно изменяющегося безнапорного движения грунтовой воды (формула Дюпюи)
- •13.5 Определение коэффициента фильтрации в лабораторных условиях
- •13.6 Дифференциальное уравнение неравномерного плавно изменяющегося движения грунтовых вод в цилиндрическом русле
- •13.7 Интегрирование дифференциального уравнения неравномерного плавно изменяющегося движения грунтовой воды
- •13.8 Приток воды к совершенной водосборной галерее
- •Величины Jср среднего уклона кривой депрессии
- •13.9 Приток грунтовой воды к круглому совершенному колодцу
- •13.10 Фильтрация воды через однородную земляную дамбу
- •14. Основы физического моделирования гидравлических явлений
- •14.1 Общие сведения
- •14.2 Понятие о подобии гидравлических явлений
- •14.3 Критерии динамического подобия
- •14.3.1 Случай, когда на жидкость действуют только силы тяжести
- •14.3.2 Случай, когда на жидкость действуют только силы трения (вязкости)
- •14.3.3 Критерии подобия, выраженные через среднюю скорость
- •.3.4 Общий случай, когда на жидкость одновременно действуют несколько разных систем сил
- •14.4 Основные указания для моделирования гидравлических явлений
- •Требуемое для достижения динамического подобия отношение характеристики модели к соответствующей характеристике натуры
- •14.5. Пересчет модельных данных на натуру
- •1. Предмет гидрологии. Круговорот воды.
- •2. Основные элементы речных систем
- •3. Тип питания рек. Фазы водного режима.
- •4. Факторы стока воды.
- •5. Режим уровней воды в водотоках.
- •6. Ледовый режим рек
- •7. Закономерности движения воды в реках
- •8. Режим твердого стока
- •9. Русловой процесс
- •10. Инженерная гидрометрия
- •Список литературы
6.1 Потери напора при резком расширении напорного трубопровода (формула Борда).
На рисунке показан случай, когда труба, имеющая диаметр D1, переходит в трубу, имеющую больший диаметр D2 (D2> D1).

Струя, выходящая из первой трубы, на некоторой длине lв (в связи с наличием продольных сил трения, действующих на боковой её поверхности) расширяется и в сечении 2’-2’ заполняет всё сечение второй трубы. На длине lв струи имеет место её отрыв от стенок и образование водоворотной зоны А, имеющей в данном случае кольцевую форму. Струя между сечениями 1-1 и 2-2 может иметь несимметричный вид. На протяжении расширяющейся струи и переходного участка (между сечениями 2’-2’ и 2-2) получаем неравномерное движение, местами резко изменяющееся.
Между сечениями 1-1 и 2-2 возникает местная потеря напора hj. Эту потерю напора назовём потерей напора на резкое расширение (р.р.) потока и далее будем обозначать её через (hj)р.р. или просто через hр.р.. Впервые расчётную зависимость для hр.р. получил французский военный инженер Борда в 18 веке, который уподобил резкое расширение струи явлению удара неупругих твёрдых тел. В связи с этим потерю hр.р. иногда называют потерей напора на удар.
Выведем формулу Борда, пользуясь гидравлическим уравнением кинетической энергии (уравнение Бернулли) и гидравлическим уравнением количества движения (рассматривая эти два уравнения как систему уравнений). Решая совместно эти два уравнения, получаем возможность выделить работу внутренних сил трения, обусловливающих искомую потерю напора.
Соединим сечения 1-1 и 2-2 уравнением Бернулли. В результате получаем

Для
упрощения рассуждений будем рассматривать
только горизонтальную трубу. В районе
сечений 1-1 и 2-2 имеем равномерное движение
и потому коррективы кинетической энергии
 и
и
 для этих сечений будем считать равными
единице. При этом (6.1) перепишем в виде:
для этих сечений будем считать равными
единице. При этом (6.1) перепишем в виде:

Разность
давлений ( найдём, пользуясь гидравлическим
уравнением количества движения, которое
приложим к отсеку abcd,
соединив этим уравнением сечения 1-1 и
2-2.
найдём, пользуясь гидравлическим
уравнением количества движения, которое
приложим к отсеку abcd,
соединив этим уравнением сечения 1-1 и
2-2.
Проекция на произвольно намеченную ось S приращения количества движения δ(КД) движущегося тела равна сумме проекций на ось S импульсов внешних сил (ИС), действующих на тело, за соответствующий промежуток времени. Данную теорему условно можно написать в виде:

или в рассматриваемом случае

где
 - корректив количества движения, который
для сечения 1-1 и 2-2 примем равным единице;
- корректив количества движения, который
для сечения 1-1 и 2-2 примем равным единице;
 - проекция на направление движения
внешней силы трения Т0,
действующей со стороны стенок трубы на
рассматриваемый отсек жидкости abcd.
Так как длина участка потока между
сечениями 1-1 и 2-2 невелика, то силой Т0
пренебрегаем и считаем, что
- проекция на направление движения
внешней силы трения Т0,
действующей со стороны стенок трубы на
рассматриваемый отсек жидкости abcd.
Так как длина участка потока между
сечениями 1-1 и 2-2 невелика, то силой Т0
пренебрегаем и считаем, что
 (первое
допущение);
– проекция собственного веса отсека
на направление движения,
(первое
допущение);
– проекция собственного веса отсека
на направление движения,
 ;
;
 - сумма проекций на ось S
сил гидродинамического давления
- сумма проекций на ось S
сил гидродинамического давления
 ,
действующих соответственно на торцовые
сечения 1-1 и 2-2 выделенного отсека
транзитной струи (со стороны жидкости,
находящейся слева и справа от этого
отсека);
,
действующих соответственно на торцовые
сечения 1-1 и 2-2 выделенного отсека
транзитной струи (со стороны жидкости,
находящейся слева и справа от этого
отсека);
 – проекция на направление движения
реакции стенок (без учёта сил трения);
величина
– проекция на направление движения
реакции стенок (без учёта сил трения);
величина
 ,
где сила
,
где сила
 - давление вертикальной стенки ad,
имеющей кольцевую форму, на жидкость.
- давление вертикальной стенки ad,
имеющей кольцевую форму, на жидкость.
Величину
 можно представить в виде
можно представить в виде

Поскольку в сечении 2-2 мы имеем равномерное движение, то давление в нём распределяется по гидростатическому закону. Примем, что давление по всему сечению 1-1 (по площади ad, охватывающей транзитную струю и водоворотную область) распределяется также по гидростатическому закону (второе допущение). При этом можем написать:

где
 – гидродинамические давления в центрах
тяжести сечений 1-1 (круга ad)
и 2-2 (круга bc);
– гидродинамические давления в центрах
тяжести сечений 1-1 (круга ad)
и 2-2 (круга bc);
 - площадь сечения второй трубы. Подставляя
(6.6) и (6.7) в (6.5), находим:
- площадь сечения второй трубы. Подставляя
(6.6) и (6.7) в (6.5), находим:

Учитывая (6.8), уравнение (6.4) переписываем в виде.

Откуда, имея в виду, что

получаем

Подставляя (6.10) в (6.2), имеем:

или окончательно

где
разность
 называют потерянной скоростью. Формула
(6.12) называется формулой Борда. Согласно
этой формуле потеря напора при резком
расширении равняется скоростному
напору, отвечающему потерянной скорости.
называют потерянной скоростью. Формула
(6.12) называется формулой Борда. Согласно
этой формуле потеря напора при резком
расширении равняется скоростному
напору, отвечающему потерянной скорости.
Преобразование формулы Борда
Вынесем за скобки, тогда получим:

Обозначая

имеем

где
 - коэффициент сопротивления при резком
расширении потока.
- коэффициент сопротивления при резком
расширении потока.
Местная потеря напора, получающаяся при выходе потока из трубы в бассейн больших размеров.
Эту
потерю называют потерей «на выход», её
обозначают через
 .
Данный случай является частным случаем
предыдущего, когда
значительно больше
.
Данный случай является частным случаем
предыдущего, когда
значительно больше
 ,
(
,
( ).
Имея это в виду, можем написать в
соответствии с формулой (6.14), что
).
Имея это в виду, можем написать в
соответствии с формулой (6.14), что

а следовательно потеря на выход будет