3.3 Законы внутреннего трения в жидкости. Величина касательных напряжений трения при ламинарном движении жидкости.

Представим некоторое живое сечение и соответствующую ему эпюру скоростей АВС. Покажем далее два слоя жидкости (заштрихованы на чертеже), из которых первый слой движется со скоростью u₁, а второй слой со скоростью u₂. Поверхность соприкосновения этих слоёв имеет площадь S. По этой поверхности в реальной жидкости развиваются парные силы внутреннего трения Т₁, приложенная к первому слою со стороны второго и Т₂, приложенная ко второму слою со стороны первого. Очевидно, что .

Рис. 3.4

Первый слой, движущийся с большей скоростью, за счет сил трения по поверхности 1-1 способствует ускорению движения второго слоя; второй слой, наоборот, благодаря силам трения тормозит первый.

Рассмотрим параллельноструйный поток жидкости. Ограничимся рассмотрением только продольных касательных сил трения, действующих вдоль линий тока.

Законы продольного внутреннего трения, относящиеся к такому случаю движения, были установлены Ньютоном в 1686 году. Эти законы можно сформулировать так:

Сила Т продольного внутреннего трения в параллельноструйном потоке жидкости, то есть сила трения, возникающая при скольжении отдельных прямолинейных слоёв жидкости друг по другу:

1. прямо пропорциональна так называемому градиенту скорости;

2. прямо пропорциональна площади S поверхности соприкасания данных слоёв жидкости;

3. не зависит от давления;

4. зависит от физических свойств жидкости (от рода жидкости и её температуры).

Законы Ньютона можно представить в аналитической форме:

где - динамический коэффициент вязкости. Он зависит от рода жидкости, а также от её температуры, измеряется в пуазах [П].

1 П =1

Динамический коэффициент вязкости определяется с помощью специальных приборов – вискозиметров.

- градиент скорости, т.е. производная от значения скорости по нормали n, проведённой к поверхности 1-1 соприкасания слоёв жидкости.

где - угол, образованный вертикалью и касательной к кривой ВС эпюры скоростей в точке, лежащей на линии 1-1. Поскольку величина в зависимости от выбранного направления n может быть положительной или отрицательной, в дальнейшем под будем понимать её абсолютное значение.

Касательные напряжения продольного внутреннего трения для ламинарного режима при прямолинейном движении представляются в соответствии с зависимостью (3.17) в следующем виде:

Рассмотрим теперь поверхность дна D-D потока. У самой стенки u = 0. Градиент скорости у стенки равен:

Имея это в виду, силу T₀ и напряжение трения на стенке в случае ламинарного режима можно представить зависимостями:

где S₀ – площадь смоченной поверхности стенки.

Для воды при температуре 20°С: ν = 0,01 Ст или 0,01 см²/с; η = 0,01 П или 0,01 г/(см^.с)

3.4 Распределение скоростей u по живому сечению при ламинарном равномерном установившемся движении жидкости.

Рис. 3.5

Рассмотрим напорную круглоцилиндрическую трубу, имеющую радиус r₀. Покажем кривой АСВ эпюру скоростей для живого сечения АВ. Поставим себе цель найти уравнение кривой АСВ.

Для этого внутри трубы выделим центральный круглоцилиндрический столб движущейся жидкости радиусом r. Для продольного касательного напряжения трения τ по боковой поверхности этого столба можно написать два разных выражения:

1. Согласно основному уравнению равномерного движения.

где R’ – гидравлический радиус рассматриваемого столба.

2. Согласно законам Ньютона получаем:

Здесь при выбранном направлении r величина отрицательна.

Решая совместно (3.22) и (2.24), получаем:

или

Интегрируя это уравнение, имеем:

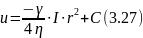
Постоянную интегрирования С находим из условия, что при r = r₀ величина u = 0.

откуда

Подставляя (3.29) в (3.27), окончательно получаем следующее уравнение, по которому можно построить кривую АСВ, ограничивающую эпюру скоростей для живого сечения АВ:

где I – пьезометрический уклон.

Как видно из (3.30), кривая АСВ является параболой. Максимальная скорость u в центре трубы будет равна u_макс

При найденной эпюре распределения скоростей u по живому сечению потока величины коррективов α₀ и α в случае ламинарного движения жидкости в круглой трубе оказываются равными: α₀ = 1,33; α = 2,0.

В целом для живого сечения эпюра скоростей будет выглядеть в виде параболоида вращения, объём которого должен равняться расходу Q.