3. Потери напора при установившемся движении жидкости.

3.1 Общие указания о потерях напора. Гидравлические сопротивления.

В дальнейшем будем изучать потерю механической энергии потоком, находящимся в неподвижном русле, обусловленную работой сил трения, возникающих в реальной жидкости при её движении.

Различают два вида потерь напора:

1) так называемую потерю напора по длине, она распределяется по длине потока равномерно (при равномерном движении) или неравномерно (при плавно изменяющемся неравномерном движении). Такую потерю напора, получающуюся на длине ℓ потока, будем обозначать через h_ℓ;

2) так называемые местные потери напора, получающиеся только в отдельных местах потока, где поток претерпевает ту или другую резкую местную деформацию. Каждую отдельную местную потерю напора будем обозначать через h_j;

При этом потери напора по длине обусловлены работой внешних и внутренних сил трения. Местные потери напора в большей степени обусловлены работой внутренних сил трения.

На рис. 3.1 представим трубопровод, имеющий особые узлы: поворот I, задвижку II (частично открытую). Помимо потери напора по длине между сечениями 1-1 и 2-2 (на участках А, Б, В), будут ещё местные потери напора: на участках Г и Д, где происходит местная деформация потока, причем как это будет пояснено ниже, в них получается резко изменяющееся неравномерное движение жидкости.

Рис. 3.1

На участке потока, где имеют место потери напора по длине, касательные напряжения τ распределяются вдоль потока равномерно или примерно равномерно; на участках же потока, где имеют место «местные потери», напряжения τ распределяются резко неравномерно.

В общем случае для участка трубопровода, заключенного между двумя сечениями, пишут:

где может быть названа полной потерей напора для рассматриваемого участка трубы.

В результате работы сил трения, представленных касательными напряжениями τ, механическая энергия, несомая жидкостью, переходит в тепло, причем жидкость нагревается; тепло с течением времени рассеивается.

Можно сказать, что величина потери напора есть мера той механической энергии жидкости, несомой единицей её веса, которая благодаря работе сил трения, распределённых равномерно по длине потока, а также сосредоточенных в отдельных его узлах (местных сил трения) переходит в тепло и безвозвратно теряется потоком.

В гидравлике часто пользуются термином «гидравлические сопротивления». Под этим термином следует понимать силы трения, возникающие в реальной жидкости при её движении.

В случае идеальной жидкости силы трения и касательные напряжения равны нулю, силы гидравлического сопротивления отсутствуют. Чем больше силы трения в реальной жидкости, тем больше при прочих равных условиях потери напора . Зная распределения в потоке касательных напряжений τ, а также скоростей u (дающих нам величину перемещений жидкости), мы могли бы подсчитать работу сил трения и тем самым определить потерю напора. Однако такая задача бывает весьма сложной, так как зачастую поле скоростей u нам бывает неизвестным.

3.2 Основное уравнение установившегося равномерного движения жидкости для «правильных» русел. Работа сил внутреннего трения.

Обозначим через τ₀ продольное касательное напряжение трения, приложенное со стороны стенок к потоку жидкости. «Правильными» руслами принято называть такие русла, для которых τ₀ = const вдоль всего смоченного периметра русла.

Рис. 3.2.

Поставим цель найти зависимость потерь напора по длине от величины сил трения в жидкости. Представим на рисунке часть напорной круглоцилиндрической трубы длиной, равной ℓ, ограниченную сечениями 1-1 и 2-2. Ось S направим по течению жидкости в трубе. Падение пьезометрической линии на длине ℓ трубы выражает потерю напора.

Выясним все внешние силы, действующие на рассматриваемую часть потока. После этого, учитывая, что движение жидкости равномерное и установившееся, сумму проекций найденных сил на ось S приравняем нулю. В результате и получим искомое уравнение.

1. Силы, действующие на выделенную часть потока.

а. Собственный вес.

где ω – площадь живого сечения потока.

Проекция собственного веса на ось S.

где - угол наклона оси трубы к горизонту.

Из рис. 3.2 видно, что

Поэтому

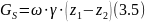
б. Силы Р₁ и Р₂ давления на торцовые сечения рассматриваемого жидкого отсека со стороны соседних отброшенных объёмов жидкости

где р₁ и р_2­ – гидродинамические давления в центрах тяжести живых сечений 1-1 и 2-2. Силы Р₁ и Р₂ проектируются на ось S без искажения.

Поскольку при движении реальной жидкости в ней возникают силы трения, то в рассматриваемой точке нормальные напряжения σ_n будут зависеть от ориентировки площадки. В гидродинамике реальной жидкости в данной точке площадок действия, имеющих разный наклон, значения σ_n будут разные.

Вместе с тем, чтобы упростить решение задач гидродинамики, здесь вводят особое понятие – понятие «гидродинамического давления в точке» и условно считают, что р в данной точке движущейся реальной жидкости, являясь также скалярной величиной (как в гидростатике), не зависит от ориентировки площадки действия и равняется:

- для пространственной задачи¹

• для плоской задачи

Как видно, в отличие от гидростатического давления p, гидродинамическое давление p выражает только некоторое среднее значение напряжений в данной точке и проектируется на ось S без искажения.

в. Проекция на ось S сил нормального давления на боковую поверхность потока со стороны стенок трубы равняется нулю.

г. Сила трения на стенке T₀, приложенная со стороны стенок трубы к боковой поверхности потока, направлена против течения и проектируется на ось S без искажения. Это силы внешнего трения. Имеются ещё силы внутреннего трения Т.

Изобразим внутри потока две соприкасающиеся струйки а и b. Покажем эти струйки на чертеже несколько раздвинутые. . Поэтому струйка а увлекает за собой струйку b. При этом к струйке b. оказывается приложенной сила трения Т_b, направленная по течению; наоборот к струйке а со стороны струйки b будет приложена сила внутреннего трения Т_a, направленная против течения.

Рис. 3.3

Силы внутреннего трения являются парными и . Сумма же работ этих сил не равна нулю, поскольку перемещения этих сил будут различными (для силы ). Именно эта работа сил внутреннего трения (совместно с работой силы внешнего трения Т₀) обуславливает потери напора.

2. Сумма проекций всех сил на ось S.

Учитывая, что движение равномерное и установившееся

Подставляя вместо , а также Р₁ и Р₂ их выражения через характеристики потока по (3.5) и (3.6), получим:

Разделив выражение (3.8) на , получим:

Левая часть уравнения (3.10) равна h_ℓ:

Тогда сила трения Т₀ для правильных русел выражается следующей зависимостью:

Тогда

где - пьезометрический уклон.

Выражение (3.15) является основным уравнением установившегося равномерного движения для «правильных» русел.

Также оно может иметь форму: