
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf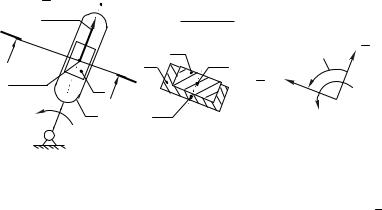
60 |
Лекция 4 |
ЛЕКЦИЯ 4
СОДЕРЖАНИЕ
2.5.Основные уравнения, связывающие скорости и ускорения двух точек, принадлежащих двум звеньям, входящих в поступательную пару.
2.6.Кинематический анализ группы Ассура класса 2 вида.
2.7.Кинематический анализ группы Ассура класса 3 вида.
Контрольные вопросы к теме 2
2.5.Основные уравнения, связывающие скорости и ускорения двух точек, принадлежащих двум звеньям, входящих в поступательную пару
Пусть точка B2 (рис.2.8,а) принадлежит звену 2, а
точка B3 звену 3. В данный момент времени точки B2 и
B3 совпадают. Точка B3 лежит под точкой B2 (рис.2.8,б).
B3B2 |
|
D |
А А |
|
|
А |
|
|
2 |
90 |
B B |
В2,B3 |
|
|
3 |
В2 |
3 2 |
3 |
2 А |
B3 |
aBк3B2 |
|
|
2, 3 |
|
2, 3 |
|||
С |
|
|
|
||
|
|
|
|
|
|
|
|
|
б) |
в) |
|
|
|
|
Рис. 2.8. |
|
|
Звенья |
2 |
и 3 образуют |
поступательную |
пару aA |
|
(СD – ось симметрии направляющих). |
|
||||

|
Раздел 2. Кинематический анализ механизмов |
61 |
||
B3 |
В рассматриваемом случае скорость |
точки |
||
геометрически |
складывается |
из |
двух |
|
скоростей – переносной и относительной. |
|
|
||
|
Переносной скоростью является |
скорость той |
||
точки звена 2, с которой в данный момент времени совпадает точка B3 (т.е. скорость B2 точки B2 ).
Относительная скорость точки B3 равна скорости звена 3 относительно звена 2. При движении
звена 3 относительно звена 2 точка B3 |
движется по прямой |
||||||
СD. Поэтому относительная |
скорость, обозначаемая |
||||||
B B , направлена по линии СD (рис.2.8). |
|||||||
3 |
2 |
|
|
|
|
|
|
|
Таким образом, формула для определения скорости |
||||||
точки B3 имеет вид: |
|
|
|
|
|
||
|
|
B |
B |
B B . |
(2.6) |
||
|
3 |
2 |
3 |
2 |
|
||
|
Ускорение точки |
|
B3 , |
как |
известно из курса |
||
теоретической механики, складывается из трех ускорений:
переносного |
a |
пер , относительного |
a |
отн |
и кориолисова |
||||||||
a |
к : |
|
|
|
|
|
|
|
|||||
|
|
|
a |
|
a |
пер |
|
a |
отн |
|
a |
к . |
(2.7) |
|
|
|
абс |
|
|
|
|
|
|
|
|||
Переносным ускорением aпер будет ускорение точки B2 звена 2, с которой в данный момент времени совпадает точка B3 , т.е. aB2 .
В относительном движении, как уже отмечалось, точка B3 движется по прямой линии СD. Поэтому в этом движении точка B3 имеет относительное ускорение
aBотн3B2 , направленное вдоль СD.

62 |
Лекция 4 |
Поэтому, применительно к рассматриваемому случаю, формула (2.7) будет иметь вид:
a |
B |
|
a |
B |
|
a |
BотнB |
|
a |
Bк |
B , |
(2.8) |
|
3 |
2 |
3 |
2 |
3 |
2 |
|
|||||||
Так как звенья 2 и 3 образуют поступательную пару, то они не имеют относительного вращения, следовательно, поворачиваются вместе и имеют одинаковые угловые скорости
2 |
3 . |
|
||
Кориолисово ускорение |
a |
Bк |
B |
, появляющееся в |
|
3 |
2 |
||
результате взаимодействия переносного и относительного движений, вычисляется по формуле:
|
|
a |
к |
2 |
2 |
|
B B |
, |
|
|
|
(2.9) |
|
|
|
|
B B |
2 |
|
|
|
|
|
|
|||
|
|
|
3 |
|
|
3 |
2 |
|
|
|
|
|
|
где B B |
– скорость относительного движения; |
|
|||||||||||
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
– угловая |
скорость |
|
переносного |
движения |
|||||||
|
|
(вращения) звена 2. |
|
|
|
|
|
|
|
|
|
||
Направление ускорения Кориолиса определяется по |
|||||||||||||
следующему правилу: вектор ускорения |
a |
Bк |
B |
направлен |
|||||||||
|
|
|
|
|
|
|
|
|
3 |
2 |
|
||
в ту сторону, в которую окажется направленным вектор скорости B3B2 относительного движения, если
его повернуть на 90 в направлении угловой скорости2 переносного движения (рис.2.8, в).
2.6. Кинематический анализ группы Ассура II
класса 2 вида
Рассмотрим определение скоростей и ускорений точек звеньев, а также угловых скоростей и ускорений звеньев группы Ассура II класса 2 вида на примере

63
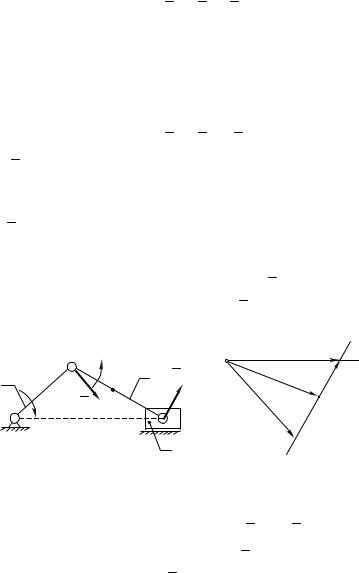
кривошипно-ползунного механизма (рис.2.9, а), в котором есть точки, принадлежащие разным звеньям, входящим в поступательную пару.
Для выполнения кинематического анализа механизма необходимо задать размеры его звеньев lOA , lAB , положение центра масс S2 (звена 2), а также значение угловой скорости 1 начального звена (кривошипа),
которую считаем постоянной ( 1 const).
В результате кинематического исследования мы должны получить скорости и ускорения точек A, B, S2 ,
величины и направления угловой скорости 2 и углового ускорения 2 звена 2.
Механизм состоит из стойки, начального звена и группы Ассура II класса 2 вида (звенья 2 и 3).
Вначале определяем скорость точки A, кривошипа
OA:
A 1 lOA.
Скорость A перпендикулярна OA и направлена в сторону угловой скорости 1.
Выбрав величину отрезка pa , которым будет изображаться вектор A, определяем масштабный коэффициент плана скоростей:
|
|
A |
. |
|
|||
|
|
(pa) |
|
На плане скоростей (рис.2.9,б) направленный отрезок pa откладывается из полюса p , перпендикулярно к звену OA.
64 |
Лекция 4 |
Точки A и B принадлежат одному звену AB, поэтому:
|
B |
A |
BA . |
(2.10) |
Точка B, кроме того, принадлежит ползуну 3, который движется поступательно в направлении BO . Следовательно, уравнение (2.6), связывающее скорости двух точек, принадлежащие двум звеньям, для данного случая имеет вид:
|
B |
B |
|
BB , |
(2.11) |
0 |
0 |
|
|||
где B0 – скорость точки B0 , принадлежащей стойке 0 и
совпадающей в данный момент с точкой B ползуна;
BB0 – скорость точки B в поступательном движении относительно точки B0 .
В этих уравнениях скорость A известна по величине и направлению, а скорость B0 0.
|
|
|
|
p,o,b |
b |
n |
|
A |
2 |
2 |
0 |
|
l |
|
BA |
|
||||
1 |
|
S2 |
s2 |
|
||
О |
|
A |
|
B |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
a |
|
|
|
|
|
|
m |
|
а) |
б) |
Рис. 2.9.
Для относительных скоростей BA и BB0 известны лишь направления: вектор скорости BA перпендикулярен к AB, а вектор скорости BB0 параллелен направляющей ползуна 3 (вдоль BO ).
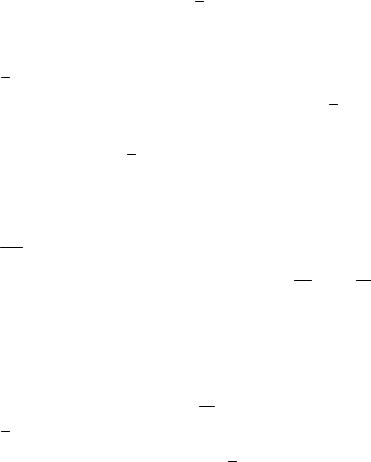
Раздел 2. Кинематический анализ механизмов |
65 |
Решаем векторные уравнения (2.10) и (2.11) |
|
графически. |
|
Согласно первому уравнению к скорости точки |
A, |
т.е. через точку "a" плана скоростей (рис.2.9,б), проводим перпендикулярно AB линию mn , вдоль которой будет направлен вектор скорости BA.
Согласно второму уравнению через точку b0 ,
совпадающую с полюсом p плана скоростей, так как
B0 0, проводим линию b0l , параллельно направляющей
BO , вдоль которой будет направлена скорость BB0 . Точка
"b" пересечений линий mn и b0l определяет конец вектора скорости B точки B.
Исходя из теоремы подобия, находим на плане скоростей точку s2 , соответствующую центру тяжести звена 2. Соединив полюс p с точкой s2 , получим отрезок
ps2 , определяющий скорость центра тяжести звена 2.
Умножив измеренные отрезки pb и ab на
масштабный коэффициент |
, |
получим значения |
|||
соответствующих скоростей: |
|
|
|
||
|
|
|
|||
|
B |
pb ; |
|
BA |
ab . |
|
|
|
|
||
Для определения направления угловой скорости звена 2 переносим вектор ab, изображающий скоростьBA на плане скоростей, в точку B механизма (рис.2.9,а).
В направлении вектора BA точка B вращается относительно точка A, следовательно, угловая скорость2 направлена против хода часовой стрелки.

66 |
Лекция 4 |
Величина угловой скорости 2 определяется из выражения:
2 BA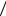 lAB .
lAB .
Переходим к определению ускорений точек и угловых ускорений звеньев механизма.
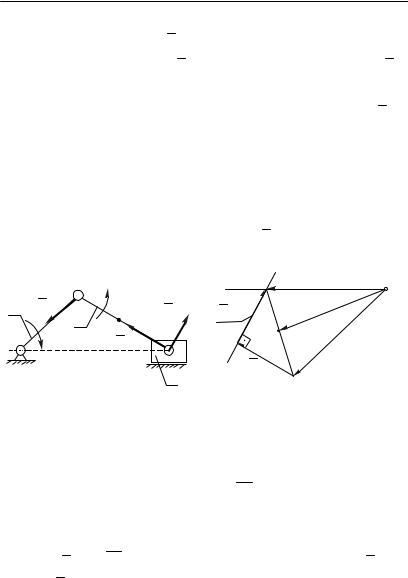
Определяем ускорение точки A. Так как звено OA вращается равномерно, то точка A имеет только нормальное ускорение, направленное по звену OA от точки A к центру вращения O (рис. 2.10,а). Величина этого ускорения равна:
aA aAn 12 lOA.
Из точки (рис.2.10,б), принятой за полюс плана ускорений, откладываем параллельно звену OA в
направлении от точки A к точке O отрезок a , соответствующий ускорению aA. Тогда масштабный коэффициент плана ускорений a будет равен:
a aA ( a).
( a).
Так как точки B и A принадлежат одному звену
AB, то:
|
|
|
|
|
a |
B |
a |
A |
a |
BA |
a |
A |
a |
BAn |
|
a |
BA , |
(2.12) |
|||||||
где |
a |
A – абсолютное ускорение точки A; |
|
|
|
|
|||||||||||||||||||
a |
BA – полное |
относительное |
ускорение |
точки |
B во |
||||||||||||||||||||
|
|
|
|
вращении её вместе со звеном 2 |
вокруг точки A; |
||||||||||||||||||||
a |
BAn – нормальное ускорение точки |
|
|
B при вращении её |
|||||||||||||||||||||
|
|
|
|
вместе |
со |
звеном |
2 |
|
|
вокруг |
точки |
A, |
|||||||||||||
|
|
|
|
направленное вдоль звена AB от точки B к |
|||||||||||||||||||||
|
|
|
|
точке A и по величине равно: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
an |
2 |
l |
AB |
|
2 |
l |
AB |
; |
|
|
|
|||||||||
|
|
|
|
|
|
BA |
2 |
|
|
|
|
AB |
|
|
|
|
|
|
|||||||
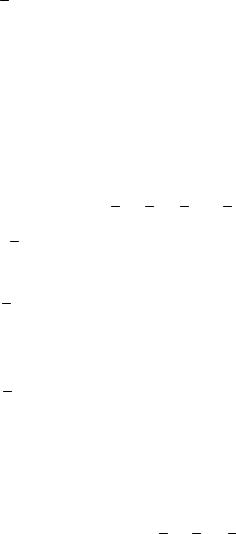
Раздел 2. Кинематический анализ механизмов |
67 |
aBA – тангенциальное ускорение точки B при её вращении вместе со звеном 2 вокруг точки A; величина этого ускорения неизвестна, известна только линия его действия, перпендикулярная к
AB.
Ползун 3, которому принадлежит точка B, совершает поступательное движение относительно стойки в направлении BO . Следовательно, уравнение (2.7), связывающее ускорения двух точек, принадлежащих разным звеньям, для данного случая имеет вид:
|
|
|
|
a |
|
a |
B |
|
a |
к |
|
a |
отн, |
|
(2.13) |
|
|
|
|
|
B |
|
|
|
|
BB |
|
|
BB |
|
|
||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
||
где |
a |
B |
– ускорение |
точки |
|
B0 , |
принадлежащей |
стойке, |
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aB |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
к |
– кориолисово |
ускорение |
точки |
B |
при её |
||||||||||
BB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
движении относительно точки B , |
aк |
0, так |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
BB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
как |
3 0 0; |
|
|
|
|
|
|
|
|
||||
a |
отн |
– ускорение точки B в поступательном движении |
||||||||||||||
|
BB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
вместе с ползуном 3 относительно стойки, |
||||||||||||||
|
|
|
||||||||||||||
|
|
|
направленное |
в |
|
направлении BO , величина |
||||||||||
|
|
|
этого ускорения неизвестна. |
|
|
|||||||||||
В связи с тем, что aBBк 0 0, уравнение (2.13)
принимает вид:
a |
|
a |
B |
|
a |
отн. |
(2.14) |
B |
|
|
|
|
BB |
|
|
|
|
|
0 |
|
|
0 |
|
Решаем векторные уравнения (2.12) и (2.14) графически.
Согласно первому уравнению к ускорению точки A, т.е. из точки "a" плана ускорений (рис.2.10,б),
68 |
|
|
|
|
Лекция 4 |
|
|
|
|
|||
параллельно AB в направлении от точки B к A |
||||||||||||
откладываем отрезок nBA , изображающий в масштабе |
||||||||||||
нормальное |
ускорение |
|
an . |
Через конец |
вектора |
n |
||||||
|
|
|
|
|
|
BA |
|
|
|
|
|
BA |
перпендикулярно к звену AB проводим линию |
ph , |
вдоль |
||||||||||
которой будет направлено тангенциальное ускорение |
|
aBA . |
||||||||||
|
Рассмотрим |
|
второе |
|
уравнение. |
b0 |
Поскольку |
|||||
ускорение |
aB |
равно |
|
нулю, |
то точка |
на |
плане |
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
ускорений совпадает с полюсом . Далее, из точки b0 |
||||||||||||
параллельно |
линии |
BO |
проводим линию d , |
вдоль |
||||||||
которой будет направлено ускорения aBB . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
,o,b0 |
||
|
A |
2 |
|
|
|
|
|
b |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
1 |
aА |
S2 |
|
a |
|
|
|
BA |
|
|
|
|
|
2 |
|
|
|
BA |
|
|
|
|
|
||
О |
1 |
aBAn |
B |
|
|
p |
s2 |
|
|
|
|
|
|
|
|
|
3 |
nBA |
|
|
|
|
|||
|
|
|
|
|
a |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
б) |
|
|
Рис. 2.10. |
Точка |
"b" |
пересечений линий ph и d |
определяет конец отрезка b, соответствующего абсолютному ускорению точки B.
Точка "b" на плане ускорений определяет так же отрезки BA и ab, изображающие тангенциальное aBA и
полное aBA относительные ускорения.
Зная положение S2 центра тяжести звена 2,
находим по правилу подобия соответствующую точку s2

Раздел 2. Кинематический анализ механизмов |
69 |
|||||||
на плане ускорений. Отрезок |
|
|
определяет величину и |
|||||
s2 |
||||||||
направление ускорения центра тяжести звена 2. |
|
|||||||
Для определения направления углового ускорения |
||||||||
2 звена 2 |
перенесем вектор |
|
BA, |
изображающий |
||||
тангенциальное |
a |
BA ускорение, |
в точку |
B (рис.2.9,а). |
||||
Видно, что угловое ускорение 2 направлено против хода часовой стрелки.
Величина углового ускорения 2 определяется из формулы:
2 aBA BA a . lAB lAB
2.7. Кинематический анализ группы Ассура II
класса 3 вида
Рассмотрим определение скоростей и ускорений точек звеньев, угловых скоростей и ускорений звеньев группы Ассура II класса 3 вида на примере кулисного механизма, изображенного на рис. 2.11,а.
Кулисный механизм содержит начальное звено 1 и группу Ассура II класса 3 вида (звенья 2,3). Внутренней парой этой группы является поступательная кинематическая пара и, кроме того, звено 3 (кулиса) совершает вращательное движение.
Вначале определяется скорость точки A вращательной кинематической пары, образованной звеньями 1 и 2 (рис. 2.11,б). Обозначают эту точку как A1,2.
Зная угловую скорость 1 звена 1, находим:
A1,2 1 lOA.
