
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
240 |
Лекция 13 |
равносмещенную систему исправления. В этом случае межосевое расстояние пары зубчатых колес равно суме делительных радиусов. Тогда условие соосности будет иметь вид:
r1 r2 |
r3 r2 , |
(6.52) |
где r1, r2, r3 и r2 – радиусы делительных окружностей зубчатых колес 1, 2 , 3 и 2 .
Используя формулу (5.2): r mz 2 , выразим радиусы делительных окружностей зубчатых колес через их модули и числа зубьев:
2 , выразим радиусы делительных окружностей зубчатых колес через их модули и числа зубьев:
mI z1 2 mI z2 |
2 mII z3 |
2 mII z2 2, (6.53) |
где mI и mII – модули пар зубчатых колес 1,2 и 2 , 3 соответственно.
Очень часто при проектировании планетарных и дифференциальных механизмов модуль для всех пар зубчатых колес принимают одинаковым mI mII m .
Тогда, после сокращения на модуль условие (6.53) соосности примет вид:
z1 z2 z3 z2. (6.54)
Таким образом, числа зубьев зубчатых колес данного планетарного механизма кроме формулы (6.32) для передаточного отношения, должны удовлетворять и условию соосности (6.54).
Если сравнить уравнения (6.52) и (6.54), то можно заметить, что условие соосности, выраженное через радиусы и через числа зубьев зубчатых колес, имеют одинаковый вид.
Для однорядного планетарного механизма (рис.6.7,а) расстояние от оси вращения колеса 1 до оси вращения сателлита 2 равно сумме радиусов делительных
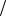
Раздел 6. Многозвенные зубчатые механизмы. |
241 |
окружностей колес 1 и 2 , а расстояние от оси вращения водила Н до оси вращения сателлита 2 равно разности радиусов делительных окружностей колес 3 и 2 . Тогда условие соосности такого механизма будет иметь вид:
z1 z2 |
z3 z2 |
или z3 z1 2z2 . |
(6.54) |
В двухрядном планетарном редукторе с внешним зацеплением (рис. 6.12,а) расстояния как от оси вращения колеса 1 до оси вращения сателлита 2 так и от оси вращения водила Н до оси вращения сателлита 2 равны сумме соответствующих радиусов, следовательно, условие соосности будет иметь вид:
z1 z2 |
z3 z2. |
(6.54) |
2. Условие соседства
Как отмечалось ранее, для уменьшения габаритов механизма, улучшения уравновешивания водила, уменьшения нагрузок на подшипники центральных колес и т.д. в планетарном редукторе устанавливают k симметрично расположенных сателлитов. В связи с этим встает вопрос о максимально возможном числе сателлитов, которые можно установить в планетарном механизме. Поскольку все сателлиты располагаются в одной плоскости, то окружности вершин зубьев сателлитов не должны пересекаться, иначе они будут задевать друг за друга.
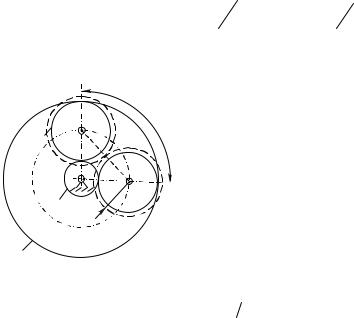
На рис. 6.19 показано предельное положение двух сателлитов с центрами в точках А и В, окружности вершин зубьев которых (пунктирные окружности) касаются.
Угол между осями сателлитов равен:
2 k. |
(6.55) |
242 |
|
|
|
|
|
Лекция 13 |
|
|
|
|
|
|
|
||||
|
|
|
|
В треугольнике ОАВ: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
АВ 2(OA)sin |
2 |
|
2(r |
r )sin |
, (6.56) |
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
k |
|
|
где r1 |
и r2 – радиусы делительных окружностей зубчатых |
||||||||||||||||
|
|
|
|
|
|
|
|
колес 1 и 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку, |
в предельном |
||||||
|
|
|
|
|
А |
положении, |
т.е. при касании |
||||||||||
2 |
|
|
окружностей |
вершин |
зубьев |
||||||||||||
|
|
|
|
|
|
|
|
|
сателлитов (рис. 6.19) радиусом |
||||||||
|
|
|
|
О |
|
ra2 , |
расстояние |
АВ 2rа2 , то |
|||||||||
|
|
|
|
В |
для |
исключения |
задевания |
||||||||||
|
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
rа2 |
||||||||||||
|
|
|
|
|
|
|
сателлитов |
друг |
|
за |
друга |
||||||
|
|
|
|
|
|
|
|
|
должно |
|
|
|
|
|
выполняться |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
неравенство |
АВ > 2ra2 |
или: |
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Рис. 6.19. |
|
|
|
|
|
> ra2 . (6.56) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
(r1 r2)sin |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
k |
||||||
|
|
|
|
Учитывая формулы |
r mz 2 |
для радиусов r1 , r2 |
|||||||||||
делительных |
окружностей и |
ra2 r2 |
m |
для |
радиуса |
||||||||||||
окружности вершин зубьев, окончательно получим:
(z |
z |
2 |
)sin |
|
> z |
2 |
2 |
. |
(6.57) |
|
|||||||||
1 |
|
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Условие (6.57), при котором сателлиты не будут задевать друг за друга, называется условием соседства. Данное условие позволяет определить максимальное число сателлитов, которые можно установить в планетарном или дифференциальном механизме.
3. Условие сборки
При сборке планетарного редуктора первый поставленный сателлит полностью определяет взаимное расположение центральных колес, и если не выполнить некоторых требований, то при установке следующих
244 |
Лекция 13 |
Так как левая часть уравнения (6.60) является целым числом, то и правая часть должна быть целым числом. Это возможно, если S1 S2 t, т.к. каждый из отрезков S1 и S2 порознь меньше t. Подставив в уравнения (6.60) S1 S2 t, получим:
z1 z3 |
k n p 1 , |
(6.61) |
или |
|
|
z1 z3 |
k P, |
(6.62) |
где P n p 1 – целое число.
Полученное условие (6.62) сборки можно сформулировать следующим образом: сумма зубьев центральных колес должна быть кратной числу сателлитов.
6.6. Комбинированные зубчатые механизмы
В машиностроении часто встречаются зубчатые механизмы, в состав которых входят одновременно рядовые, ступенчатые, планетарные и дифференциальные механизмы. Такие зубчатые механизмы называют комбинированными. При определении передаточного отношения таких механизмов необходимо сначала проанализировать их состав, определить передаточное отношение составляющих механизмов, а потом определить передаточное отношение всего комбинированного механизма в целом. Рассмотрим этот вопрос на примерах.
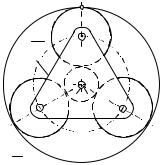
На рис.6.21 показан зубчатый механизм трасмиссии трактора К-700. Механизм включает: коробку скоростей (часть А), оси вращения зубчатых колес которой неподвижны; дифференциальный механизм на конических колесах (часть В) и конечные планетарные передачи (части С и С ).
246 |
Лекция 13 |
Определим передаточное отношение коробки скоростей на одной из передач заднего хода, если порядок включения зубчатых колес следующий: 1 5; 11 12 13; 16 19.
Зубчатый механизм, работающий на этой передаче включает: пару зубчатых колес 1 5; рядовой механизм 11 12 13, который образуется после введения в
зацепление колеса 13 при его смещении влево на III валу, и пару зубчатых колес 16 19. Все пары зубчатых колес внешнего зацепления. Передаточное отношение коробки скоростей (части А) на этой передаче равно:
UA U1,19 U1,5 U11,13 U16,19
|
1 z |
|
2 |
z |
|
1 |
z |
|
z z |
z |
|||
1 |
5 |
1 |
|
13 |
1 |
19 |
|
5 |
13 |
19 |
. |
||
z |
|
z |
z |
z z |
z |
||||||||
|
|
1 |
|
|
11 |
|
|
16 |
|
1 |
11 |
16 |
|
Передаточное отношение положительное, следовательно на этой передаче входной вал I и выходной вал IV вращаются в одну сторону.
Передаточные отношения дифференциального механизма при прямолинейной траектории движения колес трактора на вал колеса 23 и на вал колеса 23 (рис. 6.21 часть В) равны единице. Поэтому, передаточное отношение части В механизма равно передаточному отношению пары конических зубчатых колес 20 21 привода водила Н1 дифференциала:
UB U20,21 z21 z20 .
z20 .
Определим передаточное отношение части С конечного планетарного механизма. Запишем формулу Виллиса (6.21) для планетарного механизма учитывая, что солнечным является колесо 24, а опорным 26:
U24,26H U24,26H 1.

Раздел 6. Многозвенные зубчатые механизмы. |
247 |
Поскольку обращенный механизм представляет собой рядовое соединение зубчатых колес 24, 25, 26, с одним внешним (24 25) и одним внутренним (25 26) зацеплением, то
U24,26H 1 1 z26 .
z24
Тогда:
UC U24,26H 1 U24,26H 1 z26 .
z24
Передаточное отношение планетарного механизма положительное, следовательно, солнечная шестерня 24 и водило Н вращаются в одну сторону. Поскольку части С и С одинаковые, то их передаточные отношения равны.
Окончательно для передаточного отношения зубчатого механизма трансмиссии трактора на этой передаче получим:
|
|
|
|
|
|
|
|
|
|
|
z5 z13 z19 z21 |
|
|
z26 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
UI,H |
|
UA |
|
UB |
|
|
|
UC |
|
|
z z z |
z |
20 |
|
1 |
z |
24 |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 11 16 |
|
|
|
|
|
||
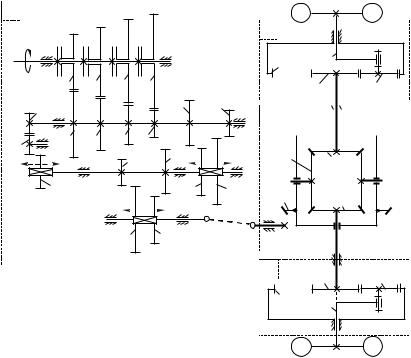
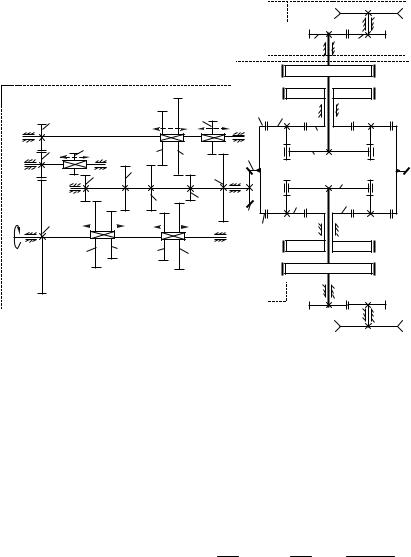
На рис.6.22 показан зубчатый механизм трасмиссии гусеничного трактора. Механизм включает: коробку скоростей (часть А), оси вращения зубчатых колес которой неподвижны; механизм поворота трактора (часть В) и конечные передачи, каждая из которых состоит из пары зубчатых колес (части С и С ).
Изменение передаточного отношения между валами I II , III II и IV II коробки скоростей (часть А) осуществляется введением в зацепление тех или иных зубчатых колес путем их осевого перемещения. Определим передаточное отношение коробки скоростей на
248 |
Лекция 13 |
одной из передач, если порядок включения зубчатых колес следующий: 1 11 13; 16 10.
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
22 |
23 |
|
|
|
|
|
|
В |
|
|
|
|
Тб2 |
А |
|
|
|
16 |
19 |
20 |
|
Тб1 |
||
13 |
|
|
|
|
|
|||||
IV |
12 |
|
|
|
|
|
|
21 |
|
|
11 |
|
15 |
14 |
18 |
|
|
Н |
|
|
|
III |
9 |
|
|
|
Н |
а |
||||
II |
|
8 |
10 |
а |
|
|
||||
|
|
7 |
6 |
|
|
|
20 |
|
|
|
|
|
|
|
1719 |
|
21 |
|
|||
1 |
|
|
|
|
|
|
|
|
||
I |
5 |
4 |
3 |
2 |
|
|
|
|
|
Тб1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
С |
|
|
|
Тб2 |
|
|
|
|
|
|
22 |
|
|||
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
Рис. 6.22. |
|
|
|
|
|
|
Зубчатый механизм, работающий на этой передаче включает: рядовой механизм 1 11 13 и пару зубчатых колес 16 10, которая образуется после введения в
зацепление колеса 16 при его смещении вправо на IV вале. Все пары зубчатых колес внешнего зацепления. Передаточное отношение коробки скоростей (части А) на этой передаче равно:
UA U1,10 U1,13 U16,10
1 2 z13 1 1 z10 z13 z10 .
z1 z16 z1 z16
Раздел 6. Многозвенные зубчатые механизмы. |
249 |
Передаточное отношение отрицательное, следовательно, на этой передаче входной вал I и выходной вал II вращаются в разные стороны.
Зубчатый механизм изображенный в части В получил название планетарного механизма поворота трактора. Механизм состоит из двух зеркально
установленных |
однорядных |
дифференциальных |
||||||||||
механизмов 19, |
20, 21, Н и |
19 |
|
, |
20 |
|
, |
|
, |
Н |
|
. |
|
|
21 |
|
|||||||||
Вращение на сблокированные центральные колеса 19, 19 дифференциальных механизмов передается через пару конических колес 17 18 от выходного вала II коробки скоростей. Выходными валами механизма поворота являются валы водил Н и Н . Управление работой каждого из дифференциальных механизмов осуществляется с помощью двух тормозных барабанов
Тб1, Тб2 и Тб1, Тб2 . Тормозные барабаны |
Тб1 и Тб1 |
||
|
|
|
, а барабаны |
соединены с центральными колесами 21 и 21 |
|||
Тб2 и Тб2 – с водилами Н и |
Н . Рассмотрим работу |
||
этого механизма. |
|
|
|
1. Включены |
тормозные |
барабаны Тб1 и Тб1. |
|
Центральные колеса |
|
|
|
21 и 21 заторможены (становятся |
|||
опорными колесами) и дифференциальные механизмы становятся планетарными. Передаточные отношения образовавшихся планетарных механизмов равны между собой и определяются по формуле Виллиса:
U19,21H U19,21H 1.
Учитывая, что обращенный механизм для планетарного представляет собой рядовое соединение зубчатых колес 19, 20, 21, с одним внутренним (19 20) и одним внешним (20 21) зацеплением, то:
U19,21H 1 1 z21 z19 .
z19 .







 А
А





 Н
Н 22
22 20
20