
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
220 |
|
Лекция 12 |
|
p5 2 |
и одну кинематическую пару В |
четвертого |
|
класса p4 |
1 , то его степень подвижности: |
|
|
|
|
W 3n 2p5 p4 3 2 2 2 1 1. |
(6.16) |
Таким образом, данный механизм относится к планетарным направляющим. Рабочий орган в таком механизме закрепляется на колесе 2. При вращении водила Н с угловой скоростью Н рабочий орган будет
двигаться по окружности радиуса ОА со скоростью VA и вращаться вокруг оси проходящей через точку А с угловой скоростью 2. Подобные движения рабочего органа используются в лопастных мешалках, хлопкоуборочных машинах, ткацких станках и т.д.
6.3. Планетарные редукторы
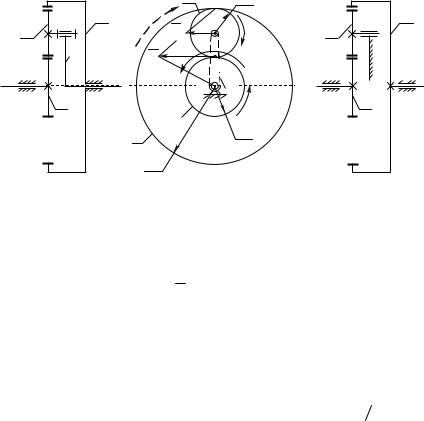
Наиболее широкое распространение планетарные зубчатые механизмы получили в планетарных редукторах, предназначенных для получения необходимых передаточных отношений. Простейший такой редуктор, состоящий из четырех звеньев (рис. 6.7,а,б), может быть получен из планетарного механизма, показанного на рис. 6.6, если в его состав ввести еще одно центральное зубчатое колесо 1, входящее в зацепление с сателлитом 2.
В данном механизме два центральных зубчатых колеса 1 и 3. Подвижное колесо 1, вокруг оси которого вращается сателлит (или сателлиты), называется солнечным, а неподвижное колесо 3 – опорным или
коронной шестерней.
Учитывая, что механизм содержит три подвижных звена: колеса 1, 2 и водило Н n 3 , три кинематические пары О, А, В пятого класса p5 3 , и две
Раздел 6. Многозвенные зубчатые механизмы. |
|
221 |
кинематические пары С и D четвертого класса p4 |
1 , |
|
то его степень подвижности: |
|
|
W 3n 2p5 p4 3 3 2 3 2 1. |
(6.17) |
|
D |
|
|
Н |
2 |
|
D |
r2 |
D |
|
|
|
А |
3 |
|
|
|
|
А |
3 |
||||
2 |
|
VA |
|
А |
2 |
2 |
|||||
С |
Н |
VC |
|
|
|
|
С |
|
|
||
|
|
|
С |
|
|
В |
|||||
|
|
|
|
|
|
|
|||||
|
|
В |
|
Н |
О |
Н |
1 |
|
|
||
О |
1 |
|
|
|
О |
1 |
|
||||
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
r1 |
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
а) |
б) |
с) |
|
Рис. 6.7. |
|
При вращении колеса 1 с угловой скоростью 1 вокруг оси, проходящей через центр кинематической пары О, точка С (полюс зацепления зубчатых колес 1 и 2)
приобретает скорость VC (рис.6.7,б). Колесо 2, которое
одновременно находится в зацеплении с опорным колесом 3, вынуждено оббегать опорное колесо, вращаясь с угловой скоростью 2 вокруг мгновенного центра вращения, совпадающего с точкой D. При этом, ось вращения колеса 2, проходящая через точку А, движется
по окружности радиуса ОА со скоростью VA VC |
2. Так |
как точка А одновременно принадлежит и водилу |
Н , то |
последнее вынужденно вращаться с угловой скоростьюН вокруг оси, совпадающей с центром кинематической пары О.
Таким образом, входным звеном механизма является солнечное колесо 1, а выходным – водило Н .
222 |
Лекция 12 |
Передаточное отношение планетарного механизма будет равно отношению угловых скоростей входного звена к выходному:
|
3 |
|
|
|
|
U |
|
|
1 |
. |
(6.18) |
1,H |
|
||||
|
|
|
|||
|
|
|
H |
|
|
При записи передаточного отношения планетарного механизма в верхнем индексе в скобках указывается номер опорного (неподвижного) зубчатого колеса.
Определение передаточного отношения планетарного механизма основывается на методе обращения движения. Этот метод состоит в следующем: всем звеньям механизма сообщается угловая скорость, равная по величине и противоположная по направлению угловой скорости водила H (на рис. 6.7,б показана пунктирной линией). Тогда водило станет неподвижным, т.е. станет неподвижной кинематическая пара А (ось вращения колеса 2). Зубчатый механизм из планетарного обратится в механизм с неподвижными осями вращения зубчатых колес, состоящий из нескольких последовательно соединенных пар зубчатых колес (рис. 6.7,с). При этом, неподвижное колесо 3 станет подвижным и будет вращаться с угловой скоростью “ H ”. Называется такой механизм обращенным.
В обращенном механизме угловые скорости зубчатых колес будут отличаться от исходного планетарного механизма:
|
|
Н |
|
|
Н |
; |
Н |
3 |
|
Н |
, |
(6.18) |
|
|
|
1 |
|
1 |
|
|
3 |
|
|
|
|||
где H |
, |
H |
– угловые скорости 1 и 3 зубчатого колеса |
||||||||||
1 |
|
3 |
|
в |
обращенном |
|
механизме |
(при |
|||||
|
|
|
|
|
|||||||||
|
|
|
|
“остановленном” водиле Н ). |
|
||||||||
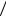
Раздел 6. Многозвенные зубчатые механизмы. |
223 |
Передаточное отношение обращенного механизма от колеса 1 к колесу 3, будет иметь вид:
|
H |
|
|
H |
|
|
|
H |
|
|
U |
1,3 |
|
1 |
|
1 |
|
. |
(6.19) |
||
|
|
|
|
|||||||
|
|
|
H |
|
|
H |
|
|||
|
|
|
3 |
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что колесо 3 в планетарном механизме неподвижное 3 0 , то:
|
|
H |
|
1 H |
|
|
|
1 |
|
|
||
|
|
U1,3 |
|
|
|
|
1 |
|
. |
(6.20) |
||
|
|
|
H |
H |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Так |
как |
отношение |
угловых |
скоростей |
1 H |
|||||||
равно |
передаточному |
отношению |
планетарного |
|||||||||
механизма U 3 |
, то: |
|
|
|
|
|
|
|
|
|
|
|
|
1,H |
U H 1 U 3 |
|
|
|
|
|
|||||
|
|
, |
|
|
|
|
||||||
|
|
1,3 |
|
|
1,H |
|
|
|
|
|
||
или |
|
U 3 |
|
|
H 1. |
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
(6.21) |
||||
|
|
1,H |
|
1,3 |
|
|
|
|
|
|
|
|
Таким образом, сумма передаточных отношений планетарного и обращенного механизмов равна единице.
Формула (6.21) носит название формулы Виллиса для планетарных механизмов и справедлива для любых планетарных механизмов при условии, что входным звеном является солнечная шестерня, а выходным – водило. В общем виде формула записывается следующим образом:
Ui,Hj |
Ui,Hj |
1, |
(6.22) |
где i, j – номера солнечной шестерни и опорного колеса соответственно.
Обращенный механизм (рис. 6.7,с) представляет собой рядовой зубчатый механизм, в котором колеса 1, 2
224 |
Лекция 12 |
образуют внешнее зацепление, а колеса 2, 3 внутреннее. Согласно формуле (6.8) его передаточное отношение равно:
|
U1,3Н |
1 1 |
z3 |
. |
|
|
|
|
|
(6.23) |
|||||||||
|
|
z1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда передаточное |
отношение |
рассматриваемого |
|||||||||||||||||
планетарного механизма (рис. 6.7,а): |
|
|
|
|
|
||||||||||||||
|
U 3 1 U |
H |
1 z |
z . |
|
(6.24) |
|||||||||||||
|
|
1,H |
|
|
|
|
1,3 |
|
|
|
|
3 |
1 |
|
|
|
|||
Если же входным звеном планетарного механизма |
|||||||||||||||||||
(рис. 6.7,а) является водило |
Н , а выходным колесо 1, то: |
||||||||||||||||||
U 3 |
|
H |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
. (6.25) |
|
|
|
|
|
|
|
|
3 |
1 z |
|
|
|||||||||
H,1 |
|
|
H |
U |
|
z |
|||||||||||||
|
1 |
|
1 |
|
1,H |
|
|
3 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
2 |
|
3 |
А |
|
Н |
||
С |
||
О |
В |
|
|
1 |
|
Рис. 6.8. |
||
В представленном на рис. 6.8 планетарном механизме входным является колесо 3, выходным водило, а опорным колесо 1. Обращенным для данного планетарного механизма будет механизм показанный на рис. 6.7,с, а передаточное отношение равно:
U3,1H |
1 U3,1H ; |
|
|
(6.26) |
||
U |
Н |
1 1 z |
z |
; |
(6.27) |
|
|
3,1 |
|
1 |
3 |
|
|
U |
1 |
1 z |
z . |
|
|
(6.28) |
|
3,H |
1 |
3 |
|
|
|
Нужно отметить, что передаточное отношение данной схемы, при любом ее включении, положительное, т.е. входной вал и выходной вал планетарного редуктора вращаются в одну сторону.
Поскольку зубчатые колеса 1, 2 и 3 стоят в один ряд, то данную схему планетарного редуктора называют

Раздел 6. Многозвенные зубчатые механизмы. |
225 |
однорядной. Коэффициент полезного действия этих передач достаточно высок, но практические диапазоны передаточных отношений ограничены по величине и определяются габаритами редуктора и конструктивными соображениями.
В таблице 6.1 приведены принятые в практике проектирования диапазоны передаточных отношений однорядного планетарного редуктора при различных включениях.
|
|
|
|
|
|
|
|
|
|
Таблица 6.1. |
Схема включения |
|
Передаточное |
|
|
Диапазон |
|||||
входноевыходноеопорное |
|
отношение |
|
|
изменения |
|||||
1 |
Н |
3 |
U |
3 |
1 z |
z |
|
|
2,3÷9 |
|
|
|
|
|
1,H |
|
3 |
1 |
|
|
|
Н |
1 |
3 |
U |
3 |
z |
z |
z |
|
0,11÷0,445 |
|
|
|
|
|
H,1 |
1 |
1 |
3 |
|
|
|
3 |
Н |
1 |
U |
1 |
1 z |
z |
|
|
1,12÷1,78 |
|
|
|
|
|
3,H |
|
1 |
3 |
|
|
|
Н |
3 |
1 |
U |
1 |
z |
z |
z |
|
|
0,56÷0,9 |
|
|
|
|
H,3 |
3 |
1 |
3 |
|
|
|
Из таблицы видно, что однорядный планетарный редуктор перекрывает с разрывами передаточные отношения от 0,11 до 9 (выпадают передаточные отношения в диапазонах от 0,9 до 1,12 и от 1,78 до 2,3).
Несмотря на то, что передаточное отношение однорядного планетарного редуктора находится на уровне передаточного отношения двухступенчатого редуктора с неподвижными осями вращения зубчатых колес, планетарный редуктор имеет свои преимущества.
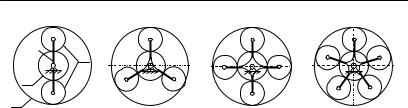
Обычно в реальном планетарном редукторе устанавливают k симметрично расположенных сателлитов (рис. 6.9).
226 |
|
Лекция 12 |
|
Н |
2 |
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
k 2 |
k 3 |
k 4 |
k 5 |
Рис. 6.9.
С точки зрения кинематического анализа (определения передаточного отношения) достаточно учесть только один сателлит, так как остальные являются пассивными в кинематическом отношении.
При передаче крутящего момента в ступенчатом механизме все усилие передается одним зубом, который в данный момент находится в зацеплении на колесе. В планетарном редукторе усилие на зуб зубчатого колеса уменьшается в k раз, так как на каждом сателлите в зацеплении находится по одному зубу. Поскольку усилие между зубьями уменьшается, то, следовательно, можно уменьшить толщину зуба (модуль зубчатого колеса). В результате, уменьшаются габариты механизма (особенно осевые), разгружаются подшипники центральных колес, улучшается уравновешивание водила, уменьшается вес механизма.
Поэтому планетарные редукторы, как правило, устанавливают на тех участках передач, где крутящий момент максимальный.
В заключение необходимо отметить, что рассмотренная схема планетарного редуктора, вследствие ее простоты, наиболее широко используется в зубчатых механизмах трансмиссий сельскохозяйственных машин.
Более сложные схемы двухрядных планетарных механизмов образуются путем применения спаренных сателлитов.
Раздел 6. Многозвенные зубчатые механизмы. |
227 |
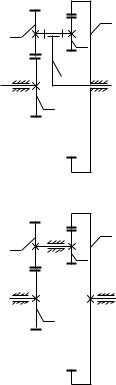
На рис. 6.10 приведена схема планетарного механизма, которая во многом повторяет ранее рассмотренную однорядную схему.
2 |
А |
3 |
|
||
|
|
2 |
|
|
Н |
|
1 |
|
Рис. 6.10. |
||
2 |
А |
3 |
|
|
|
|
|
2 |
|
1 |
|
|
Рис. 6.11. |
|
Однако, в этом механизме сателлит представляет собой два зубчатых колеса 2 и 2 , жестко насаженных на один вал. Колесо 2 находится в зацеплении с входным колесом 1, а колесо 2 – с опорным колесом 3. Выходное звено – водило
Н .
Обращенный механизм (рис. 6.11) является ступенчатым зубчатым механизмом, в котором колеса 1, 2 образуют внешнее зацепление, а колеса 2 , 3 внутреннее. Согласно формуле (6.11) его передаточное отношение от колеса 1 на колесо 3 равно:
U1,3Н |
1 1 |
z2 z3 |
. (6.31) |
|
|||
|
|
z1 z2 |
|
Тогда для планетарного редуктора получим (6.21):
U1,3H |
1 U1,3H |
1 |
z2 z3 |
.(6.32) |
|
||||
|
|
|
z1 z2 |
|
Нужно отметить, что передаточное отношение данного механизма положительное. Его характеристики во многом подобны однорядному планетарному редуктору, но диапазон возможных передаточных отношений больше
2 U1,3H 15 .
228Лекция 12
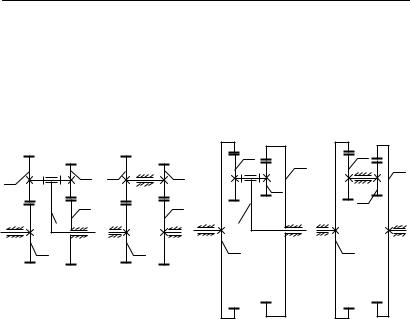
Впланетарном редукторе (рис. 6.10) сателлит входит в одно внешнее зацепление и в одно внутреннее. На рис. 6.12,а,в показаны модификации двухрядного планетарного редуктора, спаренный сателлит которого
входит |
или |
в |
два |
внешних |
зацепления |
(рис. 6.12,а) или в два внутренних (рис. 6.12,в). |
|
||||
2 |
А |
2 |
2 |
А |
2 |
|
Н |
3 |
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
а) б)
2 |
3 |
2 |
|
3 |
|
|
|
|
|
2 |
|
Н |
|
2 |
|
|
|
1 |
|
1 |
в) г)
Рис. 6.12.
Обращенные механизмы в обеих модификациях представляет собой ступенчатые зубчатые механизмы, в которых обе ступени образуют или внешнее зацепление (рис. 6.12,б) или внутреннее (рис. 6.12,г). Передаточное отношение обращенных механизмов от колеса 1 на колесо 3 будет одинаковым для обеих схем:
U |
Н |
|
z2 z3 |
. |
(6.33) |
1,3 |
|
||||
|
|
z1 z2 |
|
||
Тогда передаточное отношение этих планетарных редукторов будет равно:
U1,3H |
1 U1,3H |
1 |
z2 z3 |
. |
(6.34) |
|
|||||
|
|
|
z1 z2 |
|
|
Раздел 6. Многозвенные зубчатые механизмы. |
229 |
Из формулы (6.34) следует, что можно подобрать такие числа зубьев, при которых передаточное отношение
U |
3 |
будет |
мало отличаться |
|
от нуля. |
Например, при |
||||||||||
|
1,H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z3 101, z2 |
99, |
z2 z1 100: |
|
|
|
|
|
|
|
|
||||||
|
|
|
U |
Н |
|
z2 |
z3 |
|
|
99 101 |
|
9999 |
; |
|
||
|
|
|
|
1,3 |
|
z1 |
z2 |
100 100 |
10000 |
|
|
|||||
|
|
|
U1,3H |
1 U1,3H |
1 |
9999 |
|
1 |
. |
|||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
10000 |
10000 |
|
|||||
Однако механизм с указанным числом зубьев при входном колесе 1 практически не может быть приведен в движение вследствие самоторможения. При входном звене
– водиле Н , движение возможно, но с очень низким коэффициентом полезного действия.
Поэтому, несмотря на возможность получения очень больших или очень малых передаточных отношений, планетарные редукторы по этим схемам применяются только в маломощных передачах. Обычно входным звеном является водило, а передаточные
отношения UH3,1 выбираются в пределах от 30 до 100 (в
редких случаях до 1500). Преимущество отдается схеме с внутренним зацеплением (рис. 6.12,в), как имеющей несколько больший коэффициент полезного действия.
