
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
150Лекция 9
4.10.Силовой анализ начального звена (механизма I класса)
Принятое при анализе механизма начальное звено (механизм I класса) чаще всего совершает вращательное движение, т.е. является кривошипом. В результате выполненного силового анализа присоединенной к начальному звену группы Ассура, определена реакция в кинематической паре, которой эта группа присоединяется к начальному звену. Так, например, для механизма
изображенного на рис.4.11 реакция R12 в кинематической паре А, которой группа 2-3 присоединена к начальному звену 1, определена при силовом анализе этой группы
(рис.4.13,а).
Таким образом, на начальное звено 1 действуют
(рис. 4.14,а):
реакция R21 в точке А со стороны звена 2 на звено 1, которая равна по величине, но направлена противоположно R12 ;
реакция R01 в кинематической паре О от действия стойки на звено 1, величина и направление этой реакции неизвестны.
|
R21 |
А |
|
R21 |
|
R01 |
R01 |
hR |
А |
О |
1 |
|
|
|
|
Fy |
О |
1 |
My |
|
а) |
|
б) |
|
Рис. 4.14.
Под действием этих сил начальное звено, в общем случае, не будет находиться в равновесии. Чтобы имело

Раздел 4. Силовой анализ механизмов |
151 |
место равновесие звена 1, необходимо дополнительно к нему приложить силу Fy (рис. 4.14,а), или пару сил с моментом My (рис. 4.14,б), уравновешивающую действие
R21 и R01.
Сила Fy (момент My ) носит название
уравновешивающей силы (уравновешивающего момента).
Рассмотрим, какие же силы и моменты в машинах будут уравновешивающими.
Уравновешивающий момент на валу кривошипа рабочей машины создается двигателем (энергетической машиной), который приводит в движение данную машину. В свою очередь уравновешивающий момент на валу двигателя (энергетической машины) создается приводимой им в движение рабочей машиной.
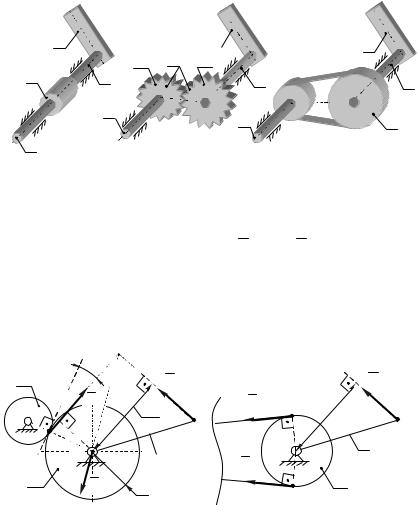
Если вал 2 кривошипа 1 рабочей машины (двигателя) соединен с главным валом двигателя (рабочей машины) 3 посредством муфты 4 (рис.4.15,а), то к кривошипу 1 будет приложен неизвестный уравновешивающий момент My и расчетная схема
начального звена имеет вид, показанный на рис.4.14,б.
Если же подвод (отвод) энергии от вала 3 к валу 2 кривошипа 1 осуществляется через зубчатую передачу 4 (рис.4.15,б), то к зубчатому колесу z1, насаженному на вал кривошипа, будет приложена неизвестная по модулю уравновешивающая F1y сила, как на рис.4.16,а.
Линия действия силы F1y определяется геометрией
зубчатой передачи – делительным радиусом r |
зубчатого |
колеса и углом зацепления W . (Вопросы |
усилий в |
152 |
Лекция 9 |
зубчатом зацеплении более подробно будут рассмотрены в разделе 5).
|
1 |
1 |
1 |
4 |
z2 |
4 z1 |
|
2 |
2 |
2 |
|
|
3 |
3 |
4 |
|
|
||
3 |
а) |
б) |
в) |
Рис. 4.15.
При ременной передаче (рис. 4.15,в) на шкив 4, насаженный на вал 2 кривошипа 1, действуют две неизвестные по модулю силы F1y и F2y (рис.4.16,б),
которые создаются натяжением ветвей ремня. Линии действия этих сил определяются положением ведущей и ведомой ветвей ремня передачи, а величины этих сил связанны между собой формулой Эйлера 1 .
z2 |
W |
|
R21 |
|
|
R21 |
F1y |
|
|
|
|||
|
hR |
А |
F |
|
hR |
|
|
h |
2y |
|
|
||
|
|
1 |
|
|
1 А |
|
|
О |
|
F1y |
О |
||
|
|
|
|
|||
z1 |
R01 |
r |
|
|
4 |
|
|
|
|
||||
|
|
|
|
|||
|
|
а) |
|
|
|
б) |
Рис. 4.16.
Таким образом, линии действия уравновешивающей силы полностью определяются конструкцией передаточного механизма от двигателя к рабочей машине.
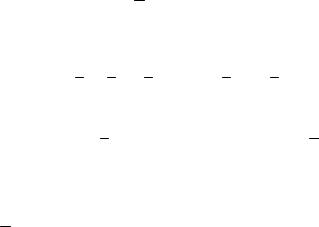
Раздел 4. Силовой анализ механизмов |
153 |
Рассмотрим случай соединения валов посредством муфты (рис.4.15,а).
Запишем уравнение равновесия моментов сил, действующих на звено 1, относительно точки О
(рис.4.14,б):
MO(Fk ) R21 hR l My 0.
1
Из этого уравнения получим величину уравновешивающего момента:
My R21 hR l ,
где l – масштабный коэффициент схемы звена 1;
hR – плечо реакции R21 относительно точки О.
Составляем геометрическое условие равновесия сил, действующих на звено 1:
Fk R21 R01 0 R01 R21.
1
Таким образом, при соединении валов посредством
муфты реакция R01 равна по модулю R21, но противоположна ей по направлению.
В случае зубчатого передаточного механизма (расчетная схема рис.4.16,а) величину уравновешивающей
силы F1y получим из уравнения равновесия моментов сил,
действующих на начальное звено, относительно точки О:
MO(Fk ) R21 hR l F1y h 0;
1
F |
|
R21 hR l |
|
R21 hR l |
, |
|
|
||||
1y |
|
h |
|
r cos W |
|
|
|
|
|||
где h r cos W .
154 |
Лекция 9 |
Величина и направление реакции R01 определяется
из геометрического условия равновесия сил, действующих на звено 1:
|
|
|
|
|
|
|
|
|
|
|
Fk |
F1y R21 R01 0. |
(4.19) |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
В уравнении (4.19) одна неизвестная величина – реакция R01. Решается уравнение построением плана сил,
подобно уравнению (4.18).
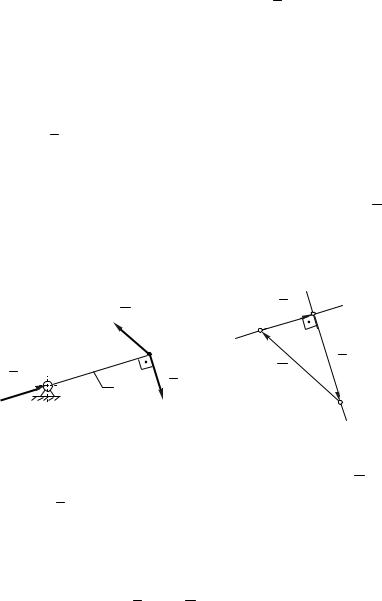
В том случае, когда конструкция передаточного механизма неизвестна, уравновешивающую силу Fy
прикладывают в точке А перпендикулярно кривошипу
ОА (рис. 4.17,а).
|
|
|
|
m |
|
|
|
|
R21 |
R |
b |
l |
|
|
|
01 |
|
|||
|
|
k a |
|
|
||
|
|
А |
|
Fy |
||
R01 |
О |
1 |
R21 |
|||
|
||||||
|
Fy |
|
p |
|||
|
|
|
|
|
||
|
|
а) |
|
б) |
n |
|
|
|
Рис. 4.17. |
|
|||
|
|
|
|
|
||
Для определения уравновешивающей силы Fy и
реакции R01 в этом случае воспользуемся известной из
теоретической механики теоремой о равновесии тела под действием трех сил, лежащих в одной плоскости. Согласно этой теореме, при равновесии тела под действием трех сил, линии действия этих сил пересекаются в одной точке.
Учитывая, что силы R21 и Fy приложены в точке А, то

|
Раздел 4. Силовой анализ механизмов |
155 |
||||||||||||||||||||
линия действия реакции |
|
|
01 |
так же должна пройти через |
||||||||||||||||||
R |
||||||||||||||||||||||
эту точку, т.е. |
линия действия реакции |
|
01 |
проходит по |
||||||||||||||||||
R |
||||||||||||||||||||||
оси кривошипа ОА. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Запишем векторное уравнение равновесия трех сил, |
|||||||||||||||||||||
действующих на звено 1: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Fk Fy R21 R01 0. |
|
(4.20) |
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решаем уравнение (4.20) |
|
путем построения плана |
|||||||||||||||||||
сил. Для этого из точки "p" |
|
(рис. 4.17,б) откладываем в |
||||||||||||||||||||
выбранном масштабе |
F силу |
|
|
21 в виде вектора |
|
|
. |
|||||||||||||||
|
R |
|
pa |
|||||||||||||||||||
|
Затем, |
через |
точку |
"p" |
|
|
проводим |
линию mn |
||||||||||||||
(перпендикулярно ОА), вдоль которой будет направлена уравновешивающая сила Fy , а через точку "a" линию kl
(параллельную ОА), вдоль которой будет направлена
реакция R01.
Пересечение этих линий в точке "b" определяет
величину и направление уравновешивающей силы Fy и
реакции R01. |
|
Из плана сил определяем: |
|
Fy (bp) F ; |
R01 (ab) F . |
Уравновешивающий момент, который будет создан на валу звена 1 передаточным механизмом:
My Fy lOA ,
где lOA – длина кривошипа.
В расчетах начального звена предполагалось, что массой кривошипа можно пренебречь, т.е. G1 0 и
Fи1 0.
156 |
Лекция 9 |
4.11. Рычаг Н.Е. Жуковского
Ранее отмечалось, что если при проведении силового анализа необходимо определить только величину уравновешивающей силы без вычисления реакций в кинематических парах, то для её определения можно воспользоваться рычагом Жуковского.
Определение уравновешивающей силы с помощью рычага Жуковского выполняется в следующей последовательности:
изобразить механизм в заданном положении и определить все внешние силы и моменты, включая силы инерции и моменты от сил инерции, действующие на его звенья;
построить в произвольном масштабе план скоростей механизма и повернуть его вокруг полюса (точки "p") на 90 в любом
направлении;
по правилу подобия на повернутом плане скоростей найти точки приложения определенных внешних сил;
в одноименных точках повернутого плана скоростей приложить силы, действующие на звенья механизма, сохраняя их направление;
если к звену механизма приложен момент, то его необходимо представить в виде пары сил, которые и перенести в соответствующие точки повернутого плана скоростей;
выбрать точку приложения |
и приложить |
||||
к |
повернутому |
|
|
плану |
скоростей |
уравновешивающую |
|
|
yж силу |
(как правило, |
|
F |
|||||
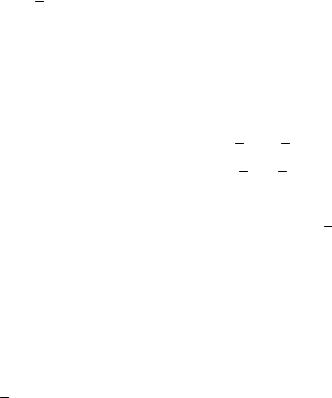
Раздел 4. Силовой анализ механизмов |
157 |
выбирают точку, в которой начальное звено присоединяется к дальнейшей схеме механизма);
рассматривая повернутый план скоростей как жесткий рычаг с точкой опоры в полюсе (точке "p"), составить уравнение равновесия этого рычага и найти величину уравновешивающей
Fyж силы.
Рассмотрим применение рычага Жуковского для нахождения уравновешивающей силы на примере кривошипно – шатунного механизма.
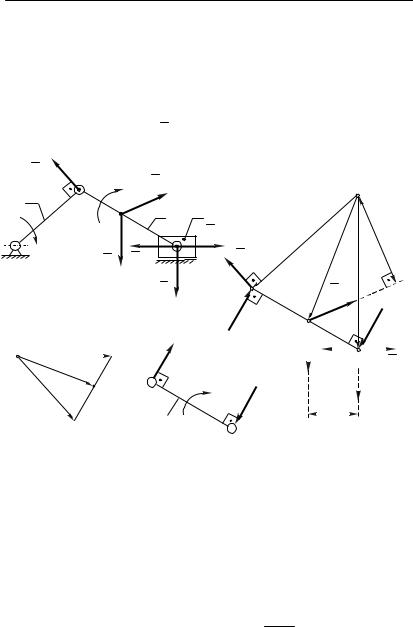
Пусть на звенья этого механизма действует система внешних сил (рис.4.18,а):
силы тяжести звеньев 2 и 3 – G2 и G3 ;
силы инерции звеньев 2 и 3 – Fu2 и Fu3 ;
момент от сил инерции звена 2 – Mи2 ;
сила производственного сопротивления – Fп.с. .
Вобщем случае под действием этих сил механизм как система, обладающая одной степенью подвижности, не находится в равновесии. Для приведения механизма в уравновешенное состояние надо в какой-либо точке механизма приложить уравновешивающую силу.
Вкачестве такой точки выберем точку А начального звена и зададимся направлением действия
силы Fyж (перпендикулярно оси кривошипа ОА).
План скоростей механизма (рис.4.18,б) поворачи-
ваем на 90 в направлении вращения начального звена 1
158 Лекция 9
(рис.4.18,г). Масштаб построения повернутого плана скоростей произвольный.
В одноименные точки повернутого плана скоростей (рис. 4.18,г) переносим, сохраняя направление, все силы, действующие на звенья механизма, в том числе и
уравновешивающую Fyж силу. |
|
|||||||
F |
ж |
A |
Mи2 |
|
|
|
|
|
y |
Fи2 |
|
|
p,o |
||||
1 |
|
|
|
|||||
|
|
|
|
2 |
|
3 |
|
|
|
|
|
S2 |
|
B |
Hи2 |
||
О |
|
|
|
|
F |
|||
|
|
|
|
|||||
1 |
|
|
|
|
|
и3 |
ж |
|
|
|
|
G |
Fп.с. |
|
F |
||
|
|
|
|
y |
||||
|
|
|
2 |
|
|
|
|
|
G3 |
a |
F |
а) |
|
и2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FMи2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mи |
|||
p,o |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||
|
|
FMи2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
2 |
|
|
F |
|
|
b F |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
s2 |
A |
|
|
|
Mи2 |
|
|
|
|
|
|
|
|
|
|
|
|
п.с. |
|
|
|
|
|
и3 |
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
Mи |
|
|
|
|
|
|
H2 |
|
G3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
б) |
|
|
|
|
|
|
в) |
|
|
|
|
|
г) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 4.18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Момент от сил инерции Mи2 представим парой сил |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
Mи2 и FM |
и2 , |
составляющие |
которой прикладываем в |
|||||||||||||||||||||||||||||
точках А и |
В звена 2, перпендикулярно АВ (рис.4.18,в). |
||||||||||||||||||||||||||||||||
Величину этих составляющих определяем из уравнения:
FMи2 FMи2 Ml и2 .
AB
Раздел 4. Силовой анализ механизмов |
159 |
||||
|
|
|
|
|
Mи2 |
Каждую составляющую пары F |
Mи2 |
и F |
|||
переносим в одноименную точку плана скоростей без изменения её направления.
Нужно отметить, что направление момента пары сил на плане скоростей может не совпадать с направлением того же момента на плане механизма.
Составляем уравнение равновесия моментов относительно полюса p всех перенесенных сил повернутого плана скоростей:
Mp(Fk ) G2 H2 Fu2 Hu2 Fи3 (pb)
Fп.с. (pb) FMи2 (ab) Fyж (pa) 0. (4. 21)
Вуравнении (4.21): H2 и Hи2 – соответственно
плечи сил G2 и |
Fu2 ; |
|
(pb) |
– плечо сил Fu3 |
и Fп.с. ; |
||||||
(pa) |
– плечо силы |
|
|
ж |
; |
(ab) |
– плечо пары сил |
F |
и |
||
F |
|||||||||||
|
|
|
|
|
y |
|
|
|
Mи2 |
|
|
|
|
Mи2 |
|
|
|
|
|
|
|
|
|
F |
(рис.4.18,г). |
|
|
|
|
|
|
|
|
||
Из уравнения (4.21) определяем величину уравновешивающей силы:
Fж |
1 |
G H |
|
F |
H |
|
F |
(pb) |
|
|
(pa) |
|
|
|
|||||||
y |
2 |
2 |
u2 |
|
u2 |
|
и3 |
|
|
|
|
|
|
|
|
F |
|
(pb) F |
(ab) . |
||
|
|
|
|
|
|
п.с. |
|
Mи2 |
|
|
Если величина уравновешивающей силы окажется положительной, то направление силы Fyж было выбрано правильно. При отрицательном значении – направление
Fyж необходимо изменить в противоположную сторону.
