
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf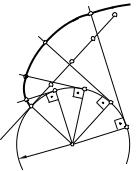
170 |
Лекция 10 |
5.4. Эвольвента круга и ее свойства
Как указывалось ранее, главная поверхность зуба является эвольвентной. Остановимся на вопросе о том, что собой представляет эвольвента круга и какими важными свойствами для зацепления она обладает.
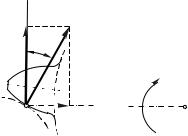
Эвольвентой круга называется траектория любой точки, например А (рис. 5.10), прямой линии n4 , которая без скольжения перекатывается по окружности радиуса rb .
Окружность радиуса rb называется основной окружностью, а прямая n4 – образующей прямой.
А4
4
А3 3 2
А2 1
1
А1 |
1 |
2 |
А0 3
n rb |
O |
4 |
|
|
|
Рис. 5.10. |
|
|
Построение эвольвенты осуществляется в следующем порядке (рис. 5.10).
Пусть задана окружность радиуса rb с центром в точке О.
Проведем к окружности касательную n4 в точке А0 и будем эту прямую
без скольжения катить по окружности.
|
Для |
построения |
эвольвенты |
круга |
делим |
отрезок |
|||||||
A04 на равные части |
(например, на четыре |
части). На |
|||||||||||
основной |
окружности |
откладываем |
дуги, |
равные |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соответствующим |
частям отрезка |
: |
|
|
|
||||||||
A04 |
A01 A01 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12 12 , |
23 23 и т.д. (при малых центральных углах |
||||||||||||
дуги можно заменить хордами). Через полученные на основной окружности точки проводим к ней касательные (перпендикуляры к радиусам O1, O2, O3, O4).
Тогда при качении прямой n4 без скольжения по окружности точки 1 , 2 , 3 , 4 прямой будут

Раздел 5. Зубчатые механизмы. |
171 |
|
|
|
|
последовательно совпадать с точками 1, 2, 3, 4 окружности. При этом точка A производящей прямой n4
будет занимать соответственно положения А1 A11 A01 ,
А2 A22 A02 , А3 A33 A03 и т.д.
Начерченная точкой A кривая A0 А4 называется
эвольвентой круга.
Эвольвента имеет две ветви, одна ветвь получается, если производящую прямую перекатывать по ходу часовой стрелки, а вторая – если против хода часовой стрелки.
Использование эвольвенты при проектировании профилей зубчатых колес объясняется совокупностью важных особенностей. Отметим основные:
эвольвента не имеет точек внутри основной окружности;
нормаль к любой точке эвольвенты направлена по касательной к основной окружности;
центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью;
эвольвента является кривой без перегибов, что важно при изготовлении режущего инструмента;
если радиус основной окружности устремить к бесконечности то и радиус кривизны эвольвенты также будет стремиться к бесконечности, т.е. эвольвента будет вырождаться в прямую линию.
5.5.Элементы эвольвентного зацепления.
1.Теоретическая линия зацепления. Допустим,
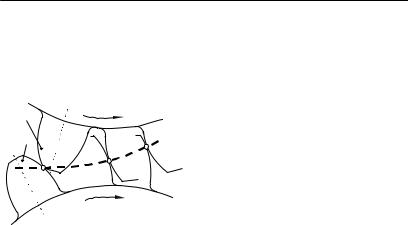
что в данный момент времени зубья двух колес касаются друг друга в точке A (рис.5.11). Если повернуть колесо 1по ходу часовой стрелки, то колесо 2 повернется против хода
172 Лекция 10
часовой стрелки. Зубья обоих колес передвинутся, и их
касание |
произойдет в новой |
точке A1 . При |
следующем |
||
повороте колеса 1 касание произойдет в точке A2 и т.д. |
|||||
|
|
|
|
Если |
объединить |
2 |
|
|
точки A, A1 , |
A2 и т.д. |
|
|
|
|
2 |
плавной кривой, то получится |
|
1 |
|
||||
|
|
||||
|
А2 |
некоторая линия, |
называемая |
||
|
|
|
|||
|
|
А |
А1 |
линией зацепления. |
|
|
|
Таким образом, линией |
|||
|
|
|
1 |
||
|
|
|
зацепления |
называется |
|
|
|
|
Рис. 5.11. |
геометрическое место точек |
|
|
|
|
касания зубьев двух колес на |
||
|
|
|
|
неподвижной плоскости. |
|
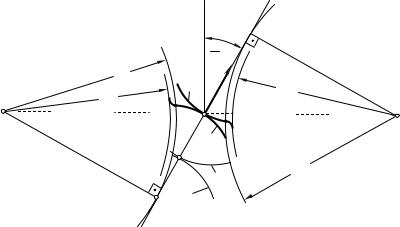
Определим вид линии зацепления в случае, если главные поверхности зубьев очерчены эвольвентами. На рис.5.12 точки О1 и О2 центры вращения зубчатых колес.
Радиусами rb1 и rb2 проведем основные окружности этих
колес и общую касательную KN к этим окружностям (точки касания A и В).
Рассмотрим, чем характерна эта линия. Если отрезок Kp (точка "p" - пересечение линий KN и О1О2 ) перекатить по основной окружности первого колеса, то точка "p"
начертит эвольвенту э1 зуба первого колеса. Если же отрезок Np перекатить по основной окружности второго колеса, то точка "p" начертит эвольвенту э2 зуба второго колеса, а касание эвольвент э1 и э2 будет находиться в точке "p".
Аналогично, для произвольной точки "с", перекатив Kс по основной окружности первого колеса, получим эвольвенту э1 зуба первого колеса, а перекатив Nс по
Раздел 5. Зубчатые механизмы. |
173 |
|
|
|
|
основной окружности второго колеса, получим эвольвенту э2 зуба второго колеса. Касание этих эвольвент будет находиться в точке "с".
N
w  B
B
rb |
э2 |
R12 |
|
1 |
rf2 |
|
|
rf1 |
O |
||
O1 |
p |
|
2 |
э1 |
|
||
|
|
|
|
|
с |
rb2 |
|
|
э1 |
э2 |
|
А |
|
|
|
K |
|
|
|
Рис. 5.12.
Отсюда можно сделать вывод о том, что точка касания эвольвентных поверхностей зубьев при вращении зубчатых колес все время находится на линии KN .
Линия AB , вдоль которой возможен контакт между зубьями зубчатых колес, находящихся в зацеплении,
называется теоретической линией зацепления. Точка "p"
пересечения теоретической линии зацепления AB с линией центров О1О2 называется полюсом зацепления.
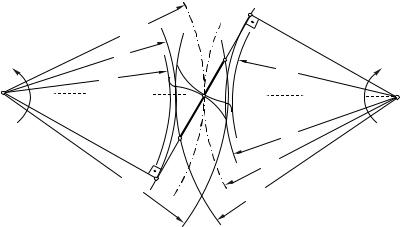
2. Практическая линия зацепления. Проведем радиусами rа1 и rа2 (рис.5.13) окружности вершин зубьев
первого и второго колеса.
Точка "a" (пересечение окружности вершин зубьев второго колеса с линией теоретического зацепления AB )
является точкой входа зубьев в зацепление. Точка "b" (пересечение окружности вершин зубьев первого колеса с
174 |
Лекция 10 |
линией теоретического зацепления AB ) является точкой выхода из зацепления зубьев, которые находились в зацеплении. (На участках Aa и bB линии теоретического зацепления соприкосновение зубьев невозможно, так как отсутствует эвольвента одного из зубьев в силу ограничения высоты зуба). Линия ab, на которой происходит соприкосновение между зубьями, называется
практической линией зацепления.
Для показанной на рис. 5.13 линии зацепления вращение первого зубчатого колеса происходит против хода часовой стрелки, а второго – по ходу. В случае изменения направлений вращения зубчатых колес, линия зацепления проходит по общей касательной к основным окружностям, для которой угол w (рис. 5.12) будет отсчитываться влево.
B |
rw1
1 |
rb1 |
b |
rf2 |
2 |
|
rf1 |
|
O |
|
O1 |
|
p |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
а |
rb2 |
|
|
rа1 |
А |
rw2 |
|
|
rа2 |
|
||
|
|
|
|
Рис. 5.13.
Согласно основной теореме зацепления [1, стр. 416] нормаль к поверхностям в точке соприкосновения элементов высшей кинематической пары качения и скольжения делит линию центров на части, обратно пропорциональные угловым скоростям.
Раздел 5. Зубчатые механизмы. |
175 |
|
|
|
|
В эвольвентном зацеплении нормаль в точке соприкосновения зубьев, которая направлена по касательной к основной окружности (вторая особенность эвольвенты), будет совпадать с линией зацепления, и пересечет линию центров О1О2 в полюсе p зацепления (рис 5.13).
Учитывая, что при вращении зубчатых колес точка "p" не меняет положения на линии центров, то
эвольвентное зацепление обеспечивает постоянное передаточное отношение (отношение угловых скоростей):
|
|
|
|
|
О p |
|
rw |
2 |
|
|
|
|
|
U |
12 |
|
|
1 |
|
2 |
|
|
. |
|
|
(5.4) |
|
|
2 |
O p |
r |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
w |
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Окружности радиусами |
rw |
и |
rw |
2 |
(рис.5.13), |
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
которые проходят через полюс зацепления |
p , |
называются |
|||||||||||
начальными окружностями.
Начальные окружности можно представить как две окружности зубчатого зацепления, которые без скольжения катятся одна по другой. Учитывая это, на начальных окружностях шаг одного зубчатого колеса равен шагу второго. Если зубчатые колеса передачи нулевые, то начальные окружности совпадают с делительными окружностями (rw1 r1, rw2 r2) .
3. Угол зацепления. Линия зацепления AB относительно перпендикуляра p к линии центров О1О2
(рис.5.12) отклонена на угол w , который называется углом зацепления.
Учитывая, что нормаль к любой точке эвольвенты направлена по касательной к основной окружности, т.е. вдоль линии зацепления, а реакция в высшей кинематической паре направлена по нормали к поверхности
176 |
|
|
|
|
|
|
|
|
|
Лекция 10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
(разд. 4.4), то усилие |
|
12 |
от первого зуба на второй будет |
|||||||||||||||||||||||
R |
||||||||||||||||||||||||||
направлено вдоль линии зацепления (рис.5.12). |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Усилие |
|
12 (рис.5.14) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
||||||||||||
|
|
|
|
|
|
|
|
|
12 |
|
раскладывается |
на |
две |
сос- |
||||||||||||
|
|
|
|
|
R |
|
||||||||||||||||||||
R |
|
|
|
|
|
|||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
тавляющие: окружную |
|
|
|
, |
|||||||||||
|
|
|
w |
|
|
|
|
|
|
|
|
R |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
которая |
|
|
вращает |
зубчатое |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
O2 |
колесо, |
и |
радиальную |
|
R |
r |
, |
|||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|||||
|
|
|
|
|
r |
которая |
|
|
воспринимается |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
R |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
12 |
|
|
|
опорами |
|
|
вала |
(подшип- |
|||||||||||||
|
|
|
|
|
|
Рис. 5.14. |
|
никами). |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Эти составляющие соответственно равны: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
cos |
w |
; |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rr |
|
R |
sin |
w |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4. |
|
|
Дуга зацепления. |
Какой |
|
либо |
зуб |
начинает |
||||||||||||||
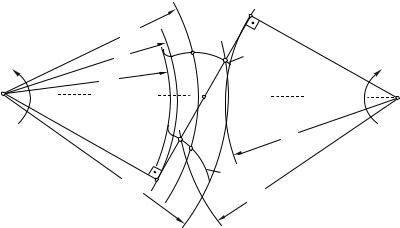
зацепление (касание с зубом второго колеса) в тот момент, когда линия его профиля эвх (рис. 5.15) проходит через
начало практической линией зацепления (точку "a"). При движении зуба точка касания будет перемещаться одновременно и по практической линии зацепления ab и по профилю зуба. Зуб заканчивает зацепление и перестает касаться зуба второго колеса, когда линия его профиля эвых
пройдет через точку "b". Эвольвента зуба эвх в точке входа зуба в зацепления и эвольвента эвых в точке выхода зуба из зацепления отсекают на делительной окружности радиусом r1 дугу сd , которая называется дугой зацепления.
Если дуга зацепления равна шагу зацепления на делительной окружности ( сd p), то при вращении колеса только одна пара профилей зубьев находится
Раздел 5. Зубчатые механизмы. |
177 |
|
|
|
|
одновременно в зацеплении. Если дуга зацепления будет меньше шага ( сd < p), то в зацеплении произойдет перерыв, и передача будет работать с ударами при входе в зацепление каждой новой пары профилей зубьев. Если, наоборот, дуга зацепления больше шага ( сd > p), то в зацеплении будет находиться всегда одна пара профилей, а в некоторые промежутки времени – две пары.
|
r1 |
B |
|
|
|
d b э |
|
|
|
|
r |
|
|
|
b1 |
вых |
2 |
||
1 |
rf1 |
|
|
|
|
|
|
O |
|
O1 |
|
p |
|
2 |
|
|
|
а |
rb |
с |
2 |
rа А |
эвх |
1 |
rа2 |
|
Рис. 5.15.
5.6. Качественные показатели зубчатого зацепления
К качественным показателям зубчатого зацепления относятся коэффициент перекрытия и удельные скорости скольжения зубьев.
1. Коэффициент перекрытия. Если первый зуб вышел из зацепления в точке b (рис. 5.15), то очевидно, что дальнейшее продолжение роботы зубчатой передачи возможно только за счет второго зуба этого колеса, следующего за первым на расстоянии шага р . При этом необходимо, чтобы второй зуб уже вошел в зацепление, т.е.

178 |
|
Лекция 10 |
|
|
|
|
|
|
|||
прошел точку а в тот момент, когда первый зуб проходит |
|||||||||||
точку b. |
|
|
|
|
|
|
|
|
|
||
|
Таким образом, при условии |
сd < p |
периодически |
||||||||
встречаются такие отрезки времени, когда в зацеплении |
|||||||||||
находится или пара зубьев, или две пары зубьев. Можно |
|||||||||||
сказать, что работа одной пары зубьев в этом случае |
|||||||||||
перекрывает работу другой пары. |
|
|
|
|
|
|
|||||
|
В соответствии с указанным, отношение дуги |
||||||||||
зацепления к шагу называется коэффициентом |
|||||||||||
перекрытия и обозначается |
: |
|
|
|
|
|
|
||||
|
|
|
|
cd cd . |
|
(5.5) |
|||||
|
|
|
|
p |
|
m |
|
|
|||
|
В |
правильно |
|
спроектированной |
передаче |
||||||
коэффициент перекрытия |
должен быть больше единицы. |
||||||||||
Обычно в прямозубой цилиндрической передаче |
|||||||||||
коэффициент перекрытия получается в пределах: |
|||||||||||
|
|
|
|
1,05 < 2. |
|
|
|
||||
|
Для |
увеличения |
|
коэффициента |
|
перекрытия |
|||||
используют передачи с косозубыми и шевронными |
|||||||||||
колесами (рис. 5.1.б,в). |
|
|
|
|
|
|
|
|
|||
|
|
В передаче с косозубыми колесами |
|||||||||
с |
e |
каждый зуб входит в зацепление не сразу по |
|||||||||
|
с |
всей длине, а постепенно. Благодаря наклону |
|||||||||
d |
зуба дуга зацепления |
сd |
по ширине колеса |
||||||||
|
|||||||||||
|
|
смещается в |
положение |
|
|
(рис. 5.16). |
|||||
|
d |
с d |
|
||||||||
|
Общая длина дуги зацепления при этом |
||||||||||
|
|
||||||||||
|
|
увеличивается на добавочную величину ec , |
|||||||||
|
которая зависит от ширины колеса b и угла |
||||||||||
|
b |
наклона зуба : |
|
|
|
|
|
|
|||
Рис.5.16. |
ed |
|
|
|
|
|
|
|
|
||
|
|
|
c d |
|
eс cd b tg . |
||||||
Раздел 5. Зубчатые механизмы. |
179 |
|||||||||
|
|
|
|
|
|
|
|
|
||
Коэффициент перекрытия |
для косозубого колеса |
|||||||||
равен: |
|
|
|
|
|
|
|
|
|
|
|
ed |
|
b |
|
b |
|
|
|||
|
|
|
cd |
|
tg |
tg , (5.6) |
||||
p |
|
|
|
|
||||||
|
|
|
p |
p |
m |
|||||
где – коэффициент перекрытия прямозубого колеса.
Коэффициент перекрытия можно рассматривать как число, показывающее, сколько пар зубьев в среднем находится в зацеплении. Так, если 1,6, то в среднем в зацеплении находится 1,6 пар зубьев, а фактически в течении 60% всего времени работы механизма в зацеплении находится две пары зубьев и в течении 40% всего времени – одна пара зубьев.
2. Удельные скорости скольжения зубьев.
|
В1 |
II |
|
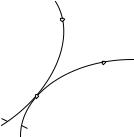
Рассмотрим две кривые |
I и |
|||||
|
|
(рис. 5.16) |
касающихся |
друг |
||||||
|
В2 |
друга. Обозначим точку касания на |
||||||||
|
кривой I |
как |
А , а |
на |
кривой |
|||||
|
А1 А |
II |
|
|
А2 . |
1 |
|
|
|
|
|
– |
как |
Через |
некоторый |
||||||
I |
2 |
промежуток |
времени эти |
кривые |
||||||
II |
||||||||||
|
будут соприкасаться в точках, |
|||||||||
|
|
|||||||||
|
Рис. 5.16. |
например В1 и В2 . |
|
|
|
|||||
|
При относительном перемещении кривых друг по |
|||||||||
другу возможны три случая: |
|
|
|
|
|
|
||||
|
1. дуга А1В1 |
равна |
дуге |
А2В2 . Такое |
движение |
|||||
называется чистым качением, т.е. кривые перекатываются друг по другу без скольжения;
2. дуга А1В1 не равна дуге А2В2 . Такое движение называется качением со скольжением.
