
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf120 |
Лекция 7 |
ЛЕКЦИЯ 7
СОДЕРЖАНИЕ
4.Силовой анализ механизмов.
4.1.Задачи силового анализа механизмов.
4.2.Методы силового анализа механизмов.
4.3.Силы инерции звеньев плоских механизмов.
4.4.Реакции в кинематических парах.
4.5.Статическая определимость кинематической цепи.
4.6.Последовательность силового анализа механизма.
4.1. Задачи силового анализа механизмов
При силовом расчете механизма обычно предполагаются заданными законы движения ведущих звеньев и часть внешних сил.
Основными силами, определяющими характер движения механизма, являются движущие силы, совершающие положительную работу, и силы полезного (производственного) сопротивления, возникающие в процессе выполнения механизмом полезной работы и совершающие отрицательную работу. К движущим силам относятся: силы давления рабочей смеси на поршень двигателя, момент, развиваемый электродвигателем на ведущем валу технологической машины, и т.д. Силы полезного сопротивления – это те силы, для преодоления которых предназначен механизм. Такими силами являются: силы сопротивления резанью в механизме жатки комбайна, силы давления газа в механизме поршневого компрессора и т.д. Кроме этих сил необходимо учитывать силы тяжести звеньев, производящие положительную или
Раздел 4. Силовой анализ механизмов |
121 |
отрицательную работу в зависимости от направления движения центра масс звеньев – вниз или вверх.
Все эти силы принято называть задаваемыми. При силовом анализе механизма движущие силы и силы производственных сопротивлений должны быть заданы. Эти силы обычно задаются в виде механических характеристик.
При работе механизма в результате действия всех приложенных к звеньям указанных сил в кинематических парах возникают реакции, которые непосредственно не влияют на характер движения механизма, но на поверхностях элементов кинематических пар вызывают силы трения. Эти силы являются силами вредного сопротивления.
Реакции в кинематических парах возникают не только вследствие воздействия внешних задаваемых сил на звенья механизма, но и вследствие движения отдельных масс механизма с ускорением. Составляющие реакций, возникающие в результате движения звеньев механизма с ускорением, называются дополнительными динамическими нагрузками.
Поэтому, первая задача силового анализа состоит
в определении реакций в кинематических парах механизмов, или, иначе говоря, давлений, возникающих в местах соприкосновения элементов кинематических пар.
Для обеспечения принятого при анализе механизма закона движения начального звена (например, равномерного) к нему необходимо приложить, или движущий момент (в технологической машине), или момент сил полезных сопротивлений от потребителей (в энергетической машине). При проведении силового анализа действие этого момента принято заменять
122 |
Лекция 7 |
приложенной к начальному звену силой, которую называют уравновешивающей. Момент этой силы относительно оси вращения начального звена равен приложенному к нему моменту.
Таким образом, вторая задача силового анализа
состоит в определении величины уравновешивающей силы.
4.2.Методы силового анализа механизмов
Втеории механизмов и машин широкое применение получил метод силового анализа механизмов основанный на принципе Даламбера:
если к каждой точке материальной системы кроме заданных внешних сил и реакций связей, приложить ещё силы инерции этой точки, то полученная система сил будет находиться в равновесии и к ней можно будет применить все уравнения статики.
Основанный на принципе Даламбера силовой метод анализа, который состоит в перенесении методов статики для решения задач динамики механизмов, называется
кинетостатическим расчетом механизмов в отличие от статического расчета, при котором силы инерции звеньев не учитываются.
Таким образом, если закон движения всех звеньев механизма известен, то, прикладывая к звеньям этого механизма кроме задаваемых сил и реакций в кинематических парах, силы инерции, можно рассматривать этот механизм условно находящимся в равновесии и определять неизвестные силы методом статики, т.е. с помощью уравнений равновесия.
Раздел 4. Силовой анализ механизмов |
123 |
Данный метод силового анализа позволяет определить реакции в кинематических парах механизма и величину уравновешивающей силы.
Если при проведении силового анализа необходимо определить только величину уравновешивающей силы без определения реакций в кинематических парах, то применяется метод силового анализа, основанный на
принципе возможных перемещений:
Согласно этому принципу, если на какую-либо механическую систему действуют силы, то, прибавляя к заданным силам силы инерции и давая всей системе возможные для данного ее положения элементарные перемещения, получаем ряд элементарных работ, сумма которых должна равняться нулю.
Отсюда вытекает, что элементарная работа уравновешивающей силы, приложенной к начальному звену, в сумме с элементарными работами всех остальных сил, действующих на звенья механизма, в том числе и сил инерции, должна быть равна нулю.
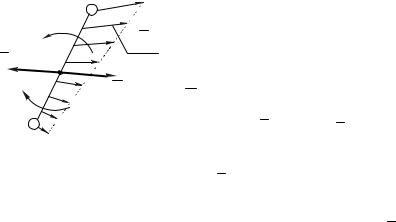
Графическая интерпретация данного метода получила название рычага Жуковского.
Рычаг Жуковского представляет собой повернутый
на 90 в любую сторону план скоростей, в одноименные точки которого, не изменяя величины и направления, перенесены все заданные силы, действующие в рассматриваемый момент времени на звенья механизма, силы инерции и уравновешивающая сила. Рассматривая повернутый план скоростей как некоторый рычаг с опорой в полюсе плана скоростей, находящийся в равновесии под действием всех приложенных сил, из уравнения моментов всех перенесенных сил относительно полюса определяется величина и направление уравновешивающей силы.
124 |
Лекция 7 |
4.3. Силы инерции звеньев плоских механизмов
Силы инерции, возникающие при движении звеньев механизма, зависят от характера движения рассматриваемого звена.
Движение звена по кинематическому признаку разделяют на три вида:
плоское;
вращательное (колебательное);
поступательное.
Звено АВ совершает плоское движение
|
|
В |
|
|
dFиi |
аS |
|
|
|
S |
|
Mи |
|
Fи |
А |
|
|
|
|
Рис. 4.1. |
Все точки звена АВ (рис.4.1) совершают движения с различными по величине и направлению ускорениями. К каждой точке звена приложена элементарная сила инерции
dFиi , равная:
|
|
dFи dmi |
ai , |
|
|
i |
|
где dmi |
– |
масса точки; |
|
ai |
– |
ускорение точки. |
|
Все элементарные силы инерции звена АВ могут быть сведены к главному вектору сил инерции – Fи ,
приложенному в центре масс S звена, и к главному моменту сил инерции – Mи (рис.4.1), величины которых равны, соответственно:
Fu m aS ; |
Mи JS , |
(4.1) |
где m – масса звена;
aS – ускорение центра масс S звена;
Раздел 4. Силовой анализ механизмов |
125 |
JS – момент инерции звена относительно оси, перпен-
дикулярной плоскости движения звена и проходящей через его центр масс S ;
– угловое ускорение звена.
Учитывая, что:
масса звена m измеряется в кг , а ускорение aS
центра масс звена – в м с2 , то модуль главного вектора сил инерции Fи будет иметь размерность:
с2 , то модуль главного вектора сил инерции Fи будет иметь размерность:
Fи m a кг м с2 Н ;
с2 Н ;
момент инерции JS имеет размерность кг м2 ,
угловое ускорение – 1 c2 , то главный момент
c2 , то главный момент
Mи сил инерции будет иметь размерность:
Ми JS кг м2 с2 Н м .
с2 Н м .
Главный вектор |
Fи |
сил инерции |
направлен |
||
противоположно направлению ускорения |
a |
S |
центра масс |
||
звена, а главный момент |
Mи |
сил инерции направлен в |
|||
сторону, противоположную направлению углового ускорения звена.
Вращательное движение звена
1. Звено вращается вокруг оси, проходящей через его центр масс (рис.4.2).
В этом случае ускорение центра масс звена равно нулю aS 0 и, следовательно, главный вектор сил инерции равен нулю:
Fи m aS 0.
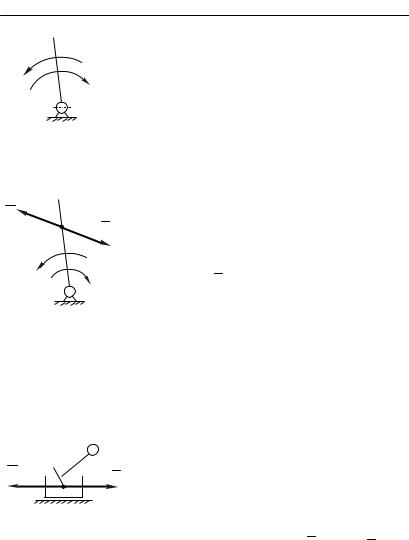
126 |
|
|
|
Лекция 7 |
|
|
|
|
|
|
|
|
Mи |
|
|
|
Если угловое ускорение звена |
не |
|||||||
|
|
равно |
нулю |
( 0), |
то |
к |
звену |
|||||
|
|
|||||||||||
|
|
прикладывается только главный момент |
||||||||||
С |
S |
|
||||||||||
|
сил инерции (рис.4.2), модуль которого |
|||||||||||
Рис. 4.2. |
|
равен: |
Mu ЈS . |
|
|
|
|
|
|
|||
2. Звено совершает вращательное движение вокруг |
||||||||||||
оси, не проходящей через его центр масс (рис.4.3). |
|
|
||||||||||
Fи |
S |
|
|
В этом случае, как и при |
||||||||
аS |
плоском |
движении |
|
звена, |
|
все |
||||||
Mи |
|
|
элементарные |
|
силы |
|
инерции |
|||||
|
|
сводятся |
к |
главному |
|
вектору |
|
сил |
||||
С |
|
инерции |
Fи |
и к |
главному моменту |
|||||||
|
|
|||||||||||
Рис. 4.3. |
|
Mи |
сил инерции, |
величины которых |
||||||||
|
определяются по формулам (4.1). |
|
|
|||||||||
|
|
|
|
|
||||||||
Поступательное движение звена
Если звено движется поступательно (рис.4.4) с ускорением, то ускорения всех его точек равны ускорению центра масс S .
С
S
Fи 
 аS
аS
Рис. 4.4.
Так как в этом случае угловое ускорение звена равно нулю 0 ,
то главный момент сил инерции равен нулю (Mи 0) и все силы инерции сведутся к главному вектору сил инерции: Fu m aS .
4.4. Реакции в кинематических парах
Реакции в кинематических парах по отношению ко всему механизму в целом являются силами внутренними, но по отношению к каждому звену, входящему в кинематическую пару, являются силами внешними.

Раздел 4. Силовой анализ механизмов |
127 |
Как было показано в разделе 1.4, в плоских кинематических цепях могут использоваться только кинематические пары IV и V классов, причем кинематические пары IV класса только высшие.
Учитывая, что реакция, как и любая другая сила, характеризуется величиной, направлением и точкой приложения, то в дальнейшем рассмотрим определение этих характеристик.
Для реакций, возникающих между элементами кинематических пар, примем следующие обозначения: реакцию со стороны звена "k" на звено "n" обозначим
как Rkn . Очевидно, что Rkn Rnk .
Рассмотрим действие сил в кинематических парах при отсутствии трения.
Высшая кинематическая пара IV класса
|
|
Как известно из теоретической механики, реакция |
|||||||||
двух |
соприкасающихся тел |
при |
отсутствии |
трения |
|||||||
|
|
|
|
|
|
|
(рис.4.5.) направлена по |
общей |
|||
|
|
|
|
|
|
n |
нормали |
к |
соприкасающимся |
||
|
|
|
|
|
|
|
поверхностям и приложена в точке |
||||
|
|
А |
|
|
12 |
их соприкосновения (точке А). |
|||||
|
|
R |
|||||||||
n |
|
|
2 |
|
Следовательно, |
в |
высшей |
||||
|
|
|
кинематической |
паре |
IV |
класса |
|||||
1 |
|
|
|
|
|||||||
|
|
Рис. 4.5. |
|
|
|
|
неизвестной |
является |
только |
||
|
|
|
|
|
|
величина реакции. |
|
|
|||
Вращательная кинематическая пара V класса
Сила взаимодействия звеньев R32, образующих низшую пару, представляет собой равнодействующую элементарных сил q32 , распределенных по поверхности соприкосновения звеньев (рис.4.6).

128 |
Лекция 7 |
R |
В |
q32 |
32 |
|
|
2

 3
3
Рис. 4.6.
Поскольку линия действия каждой из элементарных сил при отсутствии трения проходит через центр вращательной кинематической пары (точку В), то элементарные силы образует систему сходящихся сил.
Как известно из теоретической механики, систему сходящихся сил можно свести к одной результирующей
R32, точкой приложения которой будет точка пересечения линий действия элементарных сил (центр шарнира В).
Таким образом, во вращательной кинематической паре известна только точка приложения реакции, а величина и направление неизвестны, так как они зависят от величин и направлений заданных сил, приложенных к звеньям.
При силовом расчете полную
R32  R32n
R32n
 В
В
2 3
 А
А
Рис. 4.7.
реакцию R32 во вращательной
кинематической паре, например В (рис.4.7), раскладывают на две
составляющие R32n и R32 .
Составляющую реакции R32n ,
направленную по оси звена, называют нормальной реакцией, а составляющую
R32 , направленную перпендикулярно нормальной, тангенциальной реакцией.
При таком представлении реакции во вращательной паре число неизвестных не изменяется, неизвестными
только становятся величины реакций R32n и R32 .
Раздел 4. Силовой анализ механизмов |
129 |
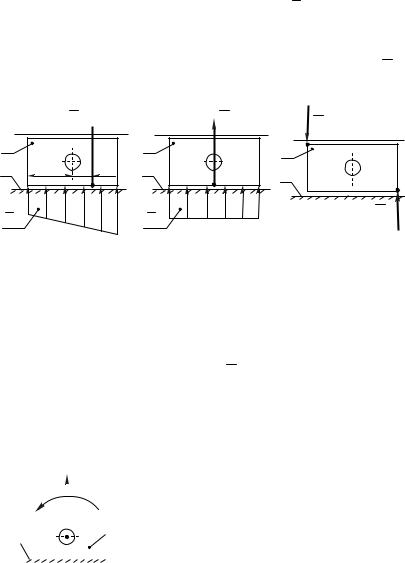
Поступательная кинематическая пара V класса
Система элементарных сил q05 (рис.4.8,а),
распределенных по поверхности соприкосновения звеньев, представляет собой систему параллельных сил, которую
можно свести к одной результирующей |
R05, |
направленной перпендикулярно опорной поверхности.
R05
5 |
|
D |
0 |
l |
b |
q05 |
а) |
|
R05 |
|
R |
|
5 |
|
|
05 |
|
D |
5 |
D |
||
0 |
||||
0 |
||||
|
||||
|
|
|
||
q05 |
|
|
|
|
|
|
R05 |
б) в)
Рис. 4.8.
Неизвестными считаются точка приложения реакции (плечо b) и её величина.
При силовом расчете, используя известную из теоретической механики лемму о параллельном переносе
силы, реакцию, например R05 (рис.4.9), сохраняя
направление, переносят в известную точку на ползуне (как правило, в центр установленного на ползуне шарнира), при этом добавляют пару сил с неизвестным моментом M05.
|
|
|
|
|
|
|
|
|
|
|
Величина |
момента M |
05 |
опре- |
||||||
M05 |
R05 |
|
|
|
|
|||||||||||||||
|
|
|
деляет |
положение |
реакции |
|
|
|
|
|||||||||||
|
|
|
|
|
|
R |
05 |
|||||||||||||
|
|
|
|
|
|
|
|
5 |
относительно |
центра |
шарнира |
|
D. |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
D |
|
|
Если |
M05 0, |
то |
линия |
действия |
||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
реакции |
|
|
будет проходить через |
|||||||
|
|
|
|
|
|
|
R |
05 |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
Рис. 4.9. |
|
|
||||||||||||||||
|
|
|
|
|
центр шарнира D (рис.4.8,б), |
а эпюра |
||||||||||||||
