
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
20 |
Лекция 2 |
ЛЕКЦИЯ 2
СОДЕРЖАНИЕ
1.4.Особенности плоской кинематической цепи.
1.5.Степень подвижности кинематической цепи.
1.6.Принцип образования механизмов.
1.7.Структурная классификация плоских
механизмов.
1.7.1.Механизм I класса.
1.7.2.Механизм II класса.
1.7.3.Механизмы III и IV классов. 1.8. Формула строения механизма.
Контрольные вопросы к теме 1
1.4.Особенности плоской кинематической цепи
Большинство механизмов используемых в сельскохозяйственных машинах принадлежат к плоским, т.е. движение их звеньев происходит в одной или нескольких параллельных плоскостях. Такое движение звеньев накладывает ряд ограничений на кинематические пары, которые могут использоваться в плоской кинематической цепи.
у |
|
B |
|
C |
|
A |
|
O |
x |
Рис. 1.7. |
|
Каждое свободное звено на плоскости обладает тремя степенями свободы (рис. 1.7): два поступательных движения вдоль осей координат Ox ,Oy и вращение в этой плоскости (вокруг оси Oz, перпендикулярной к плоскости движения звена).

Раздел 1. Структурный анализ плоских механизмов 21
Следовательно, в состав плоских кинематических цепей не могут входить кинематические пары I, II и III классов, так как число их степеней свободы более и равно (соответственно 5, 4 и 3) числа степеней свободы у тела на плоскости.
Если в составе плоского механизма использовать, например сферическую пару (таблица 1.2), которая допускает вращение вокруг трех осей координат, то будет использоваться только вращение вокруг оси Oz, а две другие степени свободы будут заблокированы схемой механизма. Таким образом, в плоской кинематической цепи сферическая пара будет соответствовать вращательной паре V класса.
Учитывая, что класс пары определяется количеством ограничений, которое накладывается на относительное движение звеньев, то пара V класса на плоскости накладывает 2 ограничения (допускает одно независимое движение), а пара IV класса – одно (допускает два независимых движения).
Используемые в плоских цепях кинематические пары IV класса могут быть только высшими. В низших парах одно из возможных движений будет блокироваться плоской кинематической цепью. Так, например, низшая цилиндрическая кинематическая пара IV класса С , образованная поверхностью поршня и стенками цилиндра двигателя внутреннего сгорания (рис. 1.1,б), допускает два независимых движения – перемещение вдоль одной оси и вращение вокруг этой оси (таблица 1.2). Плоской схемой механизма двигателя возможность вращения вокруг оси движения поршня блокируется. Поэтому эта кинематическая пара соответствует поступательной кинематической паре V класса.

22Лекция 2
Кнаиболее распространенной паре IV класса, которая широко используются в плоских механизмах, относится пара, образованная двумя цилиндрическими поверхностями с параллельными осями (рис. 1.8,а).
В этой паре один цилиндр может перекатываться по поверхности второго со скольжением, постоянно соприкасаясь по линии. Скольжение вдоль образующих цилиндров блокируется плоской схемой механизма. Эта пара в сечении плоскостью, перпендикулярной к образующим цилиндров, дает две соприкасающиеся кривые (рис.1.8,б).
1 |
|
Такая |
кинематическая |
||
|
пара имеет место, например, при |
||||
2 |
|
||||
|
соприкосновении |
зубьев |
двух |
||
|
|
зубчатых колес |
в зубчатом |
||
|
|
механизме |
или |
при |
|
а) |
б) |
соприкосновении |
ролика |
с |
|
поверхностью |
кулачка |
в |
|||
Рис. 1.8. |
|
||||
|
кулачковом механизме. |
|
|||
1.5. Степень подвижности кинематической цепи
Рассмотрим вопрос об определении степени подвижности плоской кинематической цепи (механизма).
При исследовании движений звеньев механизма рассматриваются их абсолютные перемещения относительно одного звена, которое принимают за неподвижное (стойку).
Пусть цепь (механизм) состоит из n подвижных звеньев. Если рассматривать эти звенья без связи друг с другом, то все подвижные звенья будут иметь 3n степеней свободы. Однако все звенья попарно образуют

Раздел 1. Структурный анализ плоских механизмов 23
кинематические пары, которые уменьшают число степеней свободы (возможных движений) этих звеньев.
Соединение звеньев в кинематические пары накладывает различное число ограничений на относительное движение звеньев, зависящее от класса пар.
Если число пар пятого класса равно Р5 , а число пар
IV класса – Р4 , то из 3n степеней свободы, которыми обладали звенья до их вхождения в кинематические пары, необходимо исключить те степени свободы, которые отниматься вхождением звеньев в кинематические пары. Тогда число степеней свободы W , которыми обладает кинематическая цепь, равно:
W 3n 2P5 P4 .
Записанное равенство носит название формулы подвижности или структурной формулы плоской кинематической цепи. Впервые формула была предложена П.Л.Чебышевым в 1869 году и носит его имя.
Так как механизм представляет собой кинематическую цепь со звеньями, имеющими вполне определенные движения, то необходимо выяснить вопрос о том, как связана однозначность движений звеньев механизма с его степенью подвижности. Если степень подвижности механизма равна единице, т.е. его подвижные звенья имеют одну степень свободы относительно звена, принятого за неподвижное (стойку), то достаточно одному из звеньев механизма задать вполне определенный закон движения (электродвигателем, давлением газов в цилиндре и т.д.) относительно стойки. При этом все остальные звенья механизма получат вполне определенные движения.

24Лекция 2
Вслучае, если механизм обладает двумя степенями подвижности, то необходимо задать относительно стойки по одному независимому движению двум звеньям и т.д.
Если степень подвижности равна нулю, то ни одно из звеньев не может двигаться относительно неподвижного звена и кинематическая цепь превращается в ферму, т.е. получают неподвижную конструкцию.
Следовательно, можно сказать, что механизм – это
кинематическая цепь, у которой заданы движения такому количеству звеньев, при котором все остальные звенья начали совершать вполне определенные движения.
После составления структурной схемы механизма для проектируемой машины конструктор во избежание возможных ошибок должен проверить число степеней свободы механизма. Определив число и типы кинематических пар и звеньев, следует по формуле Чебышева найти степень подвижности, которая должна соответствовать числу входных звеньев механизма и числу выбранных начальных звеньев при выполнении анализа механизма.
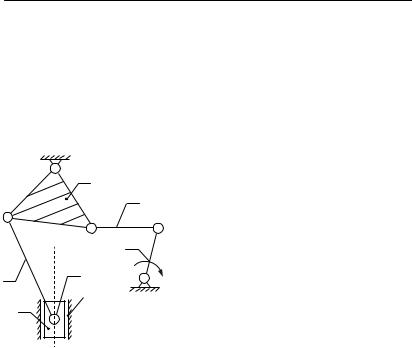
Исследуем структуру шарнирного трехзвенника, изображенного на рис. 1.9.
Число степеней свободы
Аопределим относительно одного из
3 |
звеньев, |
например |
1. |
Поскольку |
||||||
|
1 |
|
|
|
|
кинематическая |
цепь, |
присое- |
||
|
||||||||||
|
2 |
|
|
диненная к 1 звену, состоит из двух |
||||||
|
|
С звеньев |
n 2 |
и |
трех |
кине- |
||||
В |
||||||||||
|
Рис. 1.9. |
матических пар V |
класса |
P5 3, |
||||||
|
Р4 0 , то по формуле Чебышева: |
|||||||||
|
|
|
|
|
|
|||||
W 3n 2P5 P4 3 2 2 3 0.
Раздел 1. Структурный анализ плоских механизмов 25
Следовательно, шарнирный трехзвенник не имеет относительной подвижности частей и представляет собой не механизм, а одно звено. Если в дальнейшем в составе механизмов будет встречаться шарнирный трехзвенник, то его всегда будем считать за одно звено. Трехзвенник служит основой неподвижных сооружений.
D |
3 |
|
|
|
2 |
E |
С |
В |
|
1 |
|
|
|
|
4 |
F |
А |
5 |
G |
|
|
|
Рис. 1.10.
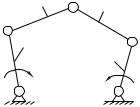
Воспользуемся формулой Чебышева для определения числа степеней свободы механизма, изображенного на рис.1.10. Механизм содержит 5 подвижных звеньев и 7 кинематических пар V класса.
Звенья 0–1, 1–2, 2–3, 0–3, 3–4 и 4–5 образуют вращательные пары A, B, C , D, E, и F , а звенья 0–5 – поступательную пару G .
Для рассматриваемого механизма
n 5, |
P4 0, |
P5 7 , |
следовательно, степень подвижности равна
W 3n 2P5 P4 3 5 2 7 1.
Как видим, рассматриваемый механизм обладает одной степенью подвижности. Это означает, что при заданном положении одного из его звеньев остальные звенья также будут занимать вполне определенные положения. Если одно из звеньев механизма заставить двигаться по какому-либо определенному закону, то все его остальные звенья также получат вполне определенные движения, являющиеся функциями заданного.
26 |
|
|
|
|
|
|
|
|
|
|
Лекция 2 |
|
|
|
|
3 |
2 |
|
|
|
Механизм |
изображенный |
|||||||
D |
|
|
||||||||||||
С |
|
|
В |
на |
рис.1.11. |
содержит |
4 |
|||||||
4 |
|
|
|
|
|
|
подвижных звена |
(n 4) и |
5 |
|||||
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
кинематических пар V класса. |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
E |
|
|
|
|
|
Звенья 0–1, 1–2, 2–3, 3–4 и 4–0 |
||||||||
|
|
|
|
А образуют вращательные пары A, |
||||||||||
|
|
|
|
Рис. 1.11. |
|
B, C , D и E (P4 0, P5 5). |
|
|||||||
Таким образом:
W 3n 2P5 P4 3 4 2 5 2.
Для однозначного определения движений звеньев такого механизма необходимо задать независимые законы движения относительно стойки двум звеньям.
1.6. Принцип образования механизмов
Основной принцип образования механизмов был впервые сформулирован в 1914 г. русским ученым Л.В.Ассуром.
Им был предложен и развит метод образования механизмов путем последовательного наслоения
кинематических цепей, обладающих определенными структурными свойствами.
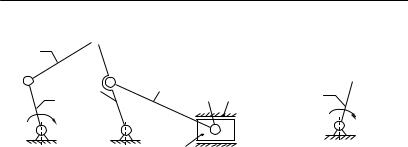
Метод Ассура проследим, рассматривая механизм грохота, изображенный на рис.1.12.
Механизм содержит 5 подвижных звеньев (1, 2, 3, 4, 5) и 7 кинематических пар V класса ( A, B, C , D, E, F , G ), т.е. n 5, P5 7 . По формуле Чебышева степень подвижности механизма равна:
W 3n 2P5 3 5 2 7 1.
Раздел 1. Структурный анализ плоских механизмов 27
2  С
С
В |
D |
3 |
|
1 |
|
А |
E |
|
4 |
G |
1 |
F |
|
|
5 |
|
А |
|
|
Рис. 1.12. Рис. 1.13.
Учитывая что, данный механизм обладает одной степенью подвижности, то достаточно привести в движение одно звено и все остальные звенья начнут совершать однозначно определяемые движения.
Теперь определим степень подвижности механизма изображенного на рис. 1.13. Механизм содержит одно подвижное звено (1) и одну кинематическую пару V класса ( A), т.е. n 1, P5 1. По формуле Чебышева степень подвижности такого механизма равна:
W 3n 2P5 3 1 2 1 1.
Если сравнить механизм грохота с рис. 1.13, то в составе грохота есть такая же группа, включающая стойку 0 и звено 1, к которой кинематической парой B присоединена кинематическая цепь, состоящая из четырех звеньев. Так как степень подвижности группы 0–1 равна единице, то, следовательно, степень подвижности кинематической цепи состоящей из звеньев 2,3,4 и 5 равна нулю.
Таким образом, механизмы образуются путем
присоединения к начальному звену и стойке (степень подвижности равна единице) кинематической цепи со степенью подвижности равной нулю.
28 |
Лекция 2 |
Кинематическая цепь с нулевой степенью подвижности носит название группы Ассура.
Группой Ассура называется кинематическая цепь с нулевой степенью подвижности относительно тех звеньев, с которыми входят в кинематические пары свободные элементы её звеньев и не распадающуюся на более простые цепи, обладающие также нулевой степенью подвижности.
Кинематическая цепь состоящая из звеньев 2, 3, 4, 5 (n 4) и кинематических пар B, C , D, E, F , G (P5 6)
механизма грохота (рис. 1.12) имеет степень подвижности равную нулю:
W 3 4 2 6 0,
но не является группой Ассура, так как она распадается на две кинематические цепи, состоящие из звеньев 2, 3 (кинематические пары B, C , E) и 4, 5 (кинематические пары D, F , G ), каждая из которых обладает нулевой степенью подвижности:
W2,3 3 2 2 3 0; |
W4,5 3 2 2 3 0. |
Процесс образования механизма грохота можно представить как последовательное присоединение к начальному звену 1 и к стойке 0 (степень подвижности равна единице) кинематической цепи BCЕ , состоящей из звеньев 2 и 3 (рис.1.14).
Полученный механизм ABCЕ , обладает одной степенью подвижности:
W 3n 2P5 3 3 2 4 1 (n 3, P5 4).
Далее, к звену 3 механизма ABCЕ и стойке 0 присоединяется кинематическая цепь DFG, состоящая из звеньев 4 и 5.
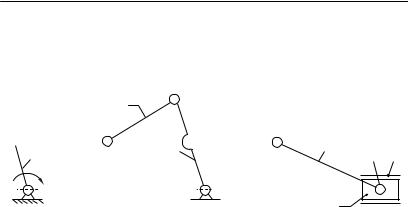
Раздел 1. Структурный анализ плоских механизмов 29
В результате получается шестизвенный механизм, обладающий одной степенью подвижности.
2 |
С |
|
|
В |
3 |
D |
|
1 |
4 F G |
||
|
А |
E |
|
5 |
||
|
||
|
Рис. 1.14. |
Следовательно, механизм, изображенный на рис.1.12, образован присоединением к начальному звену 1
истойке 0 двух групп Ассура:
первая группа состоит из звеньев 2 и 3;
вторая группа состоит из звеньев 4 и 5.
Установим закономерность образования механизма:
любой механизм имеет одно неподвижное звено (стойку – 0);
механизм должен иметь число начальных звеньев (которым задается закон движения), равное числу его степеней подвижности;
дальнейшее развитие схемы механизма происходит путем присоединения групп Ассура.
При последовательном присоединении групп Ассура необходимо руководствоваться определенными правилами.
При образовании механизма с одной степенью подвижности первая группа присоединяется свободными элементами звеньев к начальному звену и к стойке.
