
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
30 |
Лекция 2 |
Последующие группы могут присоединяться к любым звеньям полученного механизма только так, чтобы звенья группы обладали подвижностью друг относительно друга.
|
2 |
С |
|
В |
|
1 |
1 |
|
А |
3 |
D |
А |
|
а) б)
H |
2 |
E |
С |
|
3 |
||||
|
|
|||
В |
|
|
5 |
|
1 |
|
|
G |
|
|
|
4 |
||
|
|
F |
||
А |
|
D |
||
|
|
|
||
|
|
в) |
|
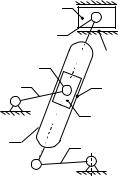
Рис. 1.15.
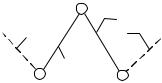
К начальному звену 1 и стойке 0 (рис.1.15,а) присоединяется группа 2–3 (рис.1.15,б). Следующая группа (4–5) присоединяется к любым двум разным звеньям механизма (например, 2 и 3), но не к одному и тому же звену. В случае EFH (рис.1.15,в) образованный звеньями контур будет жестким, т.е. будет фермой.
1.7. Структурная классификация плоских механизмов
1.7.1. Механизм I-го класса
Механизмом I-го класса условно называется
начальное звено и стойка, образующие кинематическую
1 |
|
|
|
|
|
|
|
|
пару 5 класса. |
|
|
|
||
|
|
|
А |
|
|
|
На |
рис. |
1.16 |
изображены |
||||
|
|
|
|
|
|
|
|
|||||||
А |
|
|
1 |
|
|
|
|
механизмы |
I-го |
класса, |
начальные |
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
звенья которых со |
стойкой образуют |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
а) |
|
|
|
|
|
б) |
|
вращательную |
(рис.1.16,а) |
или |
|||
|
|
|
Рис. 1.16. |
|
поступательную (рис. 1.16,б) пару. |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||

Раздел 1. Структурный анализ плоских механизмов 31
Нетрудно определить, что степень подвижности механизма I-го класса равна единице.
Изображение схемы механизма, как на рис.1.16,а, будет справедливым для электродвигателя, паровой или гидравлической турбины, центробежного насоса. У электродвигателя подвижным звеном является якорь, который вращается в опорах неподвижного корпуса. У паровой или гидравлической турбины подвижным звеном является ротор с лопатками, воспринимающими энергию струи пара или воды, который вращается в опорах неподвижного статора.
Схемное изображение парового молота, который состоит из неподвижного парового цилиндра и подвижного молота, будет соответствовать рис. 1.16,б.
Для того чтобы получить более сложные механизмы нужной степени подвижности необходимо к механизму (механизмам) I-го класса присоединить систему звеньев, представляющую одну или несколько кинематических цепей с нулевой степенью подвижности. Например, механизм грохота (рис. 1.12, 1.14) в своем составе имеет один механизм I-го класса, а механизм изображенный на рис. 1.11 – два.
1.7.2. Механизм II-го класса
Число звеньев и пар в кинематической цепи, присоединяемой к механизму I-го класса, можно определить из формулы Чебышева.
Пусть в состав кинематической цепи входят только кинематические пары V класса. Тогда степень подвижности группы Ассура равна:
WA 3n 2P5 0.
32 |
Лекция 2 |
Это уравнение является структурной формулой
группы Ассура.
Из формулы следует: |
|
|
|
|
P |
3 |
n. |
(1.1) |
|
2 |
||||
5 |
|
|
Так как числа звеньев и пар могут быть только целыми, то последнему условию удовлетворяют только следующие сочетания чисел звеньев и кинематических пар, входящих в группу (табл. 1.3).
Таблица 1.3 Сочетания чисел звеньев и кинематических пар
в группе Ассура.
№ п.п. |
1 |
2 |
3 |
4 |
n |
2 |
4 |
6 |
8 |
P5 |
3 |
6 |
9 |
12 |
Задаваясь различными сочетаниями этих чисел, можно получить группы различного вида.
Все полученные таким образом группы можно разбить по классам.
Простейшие сочетания чисел звеньев и пар, удовлетворяющих условию (1.1), будет: n 2, P5 3.
Так как любая группа после своего присоединения к начальному звену и стойке образует замкнутую кинематическую цепь, то можно сделать вывод, что число
элементов, которыми группа присоединяется, не может быть меньше двух.
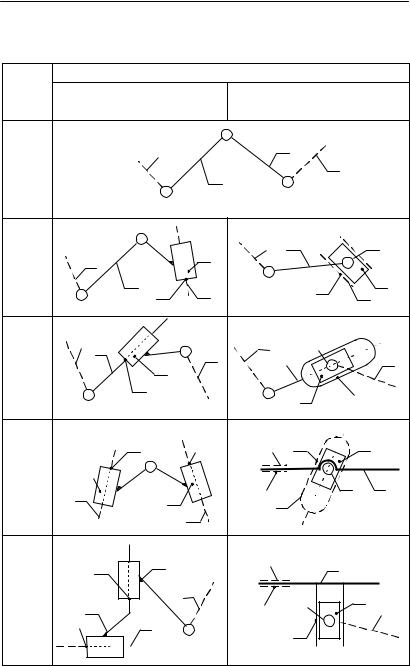
Тогда в рассматриваемой простейшей группе (n 2,P5 3) по одному элементу B и D кинематических пар на каждом звене остаются свободными, а два других
Раздел 1. Структурный анализ плоских механизмов |
|
33 |
|||||
C |
3 |
соединяются между |
собой, |
||||
образуя внутреннюю |
пару |
C |
|||||
k |
m |
||||||
|
2 |
|
группы (рис.1.17). |
|
|
|
|
|
Эта группа может |
быть |
|||||
B |
D |
||||||
присоединена элементами |
B |
и |
|||||
Рис. 1.17 |
|||||||
D к двум любым звеньям |
k |
и |
|||||
|
|
|
m механизма. |
|
|
|
|
Так как концевыми элементами B и D группа не должна присоединяться к одному и тому же звену то, при присоединении группы к одному механизму I класса элементом B группа присоединяется к начальному звену 1, а элементом D к стойке (рис. 1.15,б). Та же группа элементами B и D может быть присоединена к двум механизмам I класса (рис. 1.11), но в этом случае механизм обладает степенью подвижности, равной двум.
Группа, имеющая 2 звена и 3 кинематические пары V класса, называется группой II класса 2 порядка,
или 2-х поводковой группой, так как присоединение этой группы к основному механизму производится двумя поводками ВС и ВА.
Порядок группы определяется числом элементов, которыми группа присоединяется к основному механизму.
Группы Ассура II класса, состоящие из 2 звеньев и 3 кинематических пар, делятся на виды в зависимости от числа и расположения вращательных и поступательных пар (табл.1.4).
Группа, в состав которой входят только вращательные кинематические пары называется первым видом.
Все последующие виды группы II класса могут быть получены путем замены отдельных вращательных пар поступательными.
34 |
|
|
Лекция 2 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.4. |
||
|
Схемы групп Л. В. Ассура II |
класса |
||||||
Вид |
|
|
Схема группы |
|
|
|||
|
Общая |
|
Наиболее часто |
|||||
|
|
|
используемая |
|||||
|
|
|
|
|||||
1 |
|
1 |
B |
|
3 |
4 |
|
|
|
|
2 |
C |
|
||||
|
|
|
|
|||||
|
|
A |
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
1 |
B |
3 |
1 |
2 |
|
B |
|
2 |
|
|
|
|
|
|||
2 |
|
A |
|
|
3 |
|||
|
|
|
C |
|||||
|
A |
4 |
|
|||||
|
C |
|
|
|
4 |
|||
|
1 2 |
|
C |
1 |
2 |
B |
4 |
|
3 |
|
3 |
4 |
|
|
|||
|
|
|
|
|
|
|||
|
A |
B |
|
A |
3 |
C |
||
|
|
|
|
|||||
|
|
A |
C |
4 |
A |
|
2 |
|
4 |
2 |
B |
|
C |
|
B |
3 |
|
1 |
3 |
1 |
||||||
|
|
|
|
|
||||
|
|
|
4 |
|
|
|
|
|
|
B |
2 |
|
4 |
|
3 |
|
|
5 |
3 |
|
1 |
C |
A |
|
2 |
|
|
4 |
|
|
|
|
1 |
||
|
C |
|
|
B |
|
|
||
|
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
||

Раздел 1. Структурный анализ плоских механизмов 35
Во втором виде поступательной парой заменена одна из крайних вращательных пар A или C .
В третьем виде – поступательной парой заменена средняя вращательная пара B.
Четвертый вид – две крайние вращательные пары A и C заменены двумя поступательными парами.
Пятый вид – поступательными парами заменены крайняя C и средняя B вращательные пары.
Механизмы, в состав которых входят группы Ассура класса не выше второго, называются механизмами II класса.
Большинство современных механизмов, применяемых в технике, принадлежат к механизмам класса.
1.7.3. Механизмы III и IV классов
Второе сочетание чисел звеньев и пар: n 4, P5 6. Для этого сочетания могут быть получены два типа кинематических цепей.
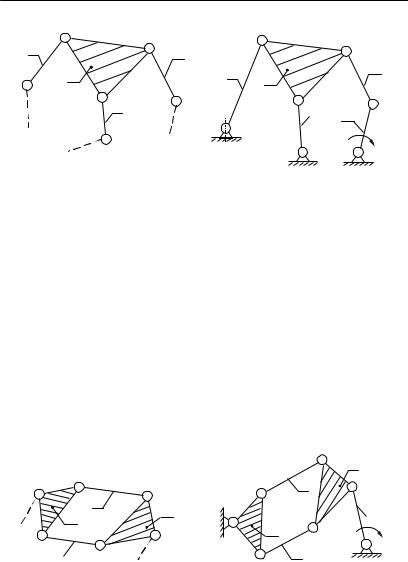
Первая кинематическая цепь, показанная на рис.1.18,а, состоит из базового звена 2 (пары С ,E,D), от которого идут три поводка 1, 3 и 4.
Такая сложная незамкнутая кинематическая цепь называется группой III класса третьего порядка. К
основному механизму группа присоединяется элементами B, H и F поводков CB, EF и DH .
Один из способов присоединения группы показан на рис. 1.18,б. Элементом пары B она присоединена к механизму I класса, а элементами пар F и H – к стойке.
36 |
|
|
Лекция 2 |
|
|
|
|
D |
|
С |
D |
|
|
|
С |
3 |
|
1 |
|
|
|
||
2 |
|
|
5 |
3 |
|
|
2 |
|
|
|
|
|
|||
H |
|
|
|
|
|
|
|
E |
4 |
В |
H |
E |
4 |
1 |
В |
|
F |
|
|
F |
|
|
|
|
|
|
|
А |
|
||
|
|
|
|
|
|
а) |
б) |
Рис. 1.18.
Механизмы, в состав которых входят группы Ассура не выше групп III класса третьего порядка, называются механизмами III класса.
Вторая возможная кинематическая цепь из четырех звеньев и шести пар показана на рис. 1.19,а.
Эта замкнутая кинематическая цепь присоединяется к другим звеньям механизма не элементами поводков, а свободными элементами В и F , принадлежащих базисным звеньям ВСЕ и FDH (рис. 1.19,б). Данная группа кроме двух базисных звеньев имеет один подвижный четырехсторонний замкнутый контур CEHD.
F |
D |
|
|
D 3 |
|
С 2 |
С |
|
|
В |
|||
|
3 |
F |
|
|
1 |
|
5 |
2 |
|
|
|||
|
5 |
|
||||
H |
|
В |
|
E |
А |
|
|
|
4 |
||||
4 |
E |
H |
||||
|
|
|
|
|
||
|
|
а) |
Рис. 1.19. |
|
б) |
|
|
|
|
|
|
|
Группа, показанная на рис. 1.19, является группой
IV класса второго порядка.

Раздел 1. Структурный анализ плоских механизмов 37
Механизмы, в состав которых входят группы Ассура не выше групп IV класса второго порядка, называются механизмами IV класса.
Если в состав механизма входят группы Ассура различных классов, то класс механизма определяется по той группе, которая относится к наивысшему классу.
Например, если механизм образован двумя группами II класса и одной группой III класса, то он должен быть отнесен к механизмам III класса.
1.8. Формула строения механизма
Как было показано выше, любой механизм независимо от его сложности и структуры может быть образован путем последовательного присоединения групп Ассура разных классов и порядков к основному механизму (механизмам) I-го класса.
Поэтому, кинематический и динамический анализ любого механизма, независимо от его сложности, может быть сведен к последовательному отделению и анализу отдельных групп Ассура, входящих в его состав.
При расчленении механизмов на группы можно рекомендовать придерживаться такой последовательности.
Сначала определяется степень подвижности механизма и выбираются начальные звенья (механизмы I-го класса). Число начальных звеньев равно степени подвижности механизма.
Разложение механизма на группы Ассура начинают с попытки выделения групп II класса. При этом необходимо каждый раз после выделения группы проверять, обладает ли оставшаяся кинематическая цепь той же степенью подвижности, что и первоначальный
38 |
Лекция 2 |
механизм, и чтобы не оставалось вообще элементов звеньев, не входящих в кинематические пары.
Если кинематическая цепь не разлагается на группы II класса, то следует переходить к группам III класса и т.д.
После выделения всех групп должны остаться стойка и звенья, выбранные начальными.
При выборе начальных звеньев нужно руководствоваться тем, что класс механизма должен быть минимальным. Класс же механизма, как было показано выше, определяется высшим классом группы Ассура, которая входит в его состав. Это объясняется тем, что чем выше класс механизма, тем сложнее его кинематический и силовой анализ.
В заключение темы рассмотрим пример структурного анализа механизма Шепинга (рис.1.20).
Состав и последовательность присоединения групп Ассура в механизме выразим формулой строения.
Механизм состоит |
из пяти |
|
|
|
подвижных |
звеньев, неподвижного |
|
5 |
|
звена – стойки и 7 кинематических |
|
F |
||
пар. |
|
|
|
|
|
|
|
E |
|
Подвижные звенья: 1 – криво- |
|
|||
|
А |
|||
шип; 2, 5 – ползуны; 3 – кулиса; 4 – |
О 1 |
В |
||
коромысло. |
Входным |
звеном, |
|
2 |
которому сообщается движение при |
|
|||
|
|
|||
работе |
механизма, |
является |
3 |
4 |
кривошип 1. Выходным звеном, |
|
|||
С |
D |
|||
совершающим требуемое движение, |
|
|||
будет ползун 5, к которому крепится
Рис. 1.20.
резец строгального станка.

Раздел 1. Структурный анализ плоских механизмов 39
Все кинематические пары механизма относятся к V
классу, |
вращательные: О(0 1); |
А(1 2); |
С(3 4); |
D(4 0); |
F(3 5), поступательные: |
B(2 3); E(5 0). |
|
По формуле Чебышева степень подвижности механизма равна:
W 3n 2P5 3 5 2 7 1,
т.е. механизм обладает одной степенью подвижности и,
следовательно, должен иметь одно начальное звено
(механизм I класса).
За начальное звено, связанное со стойкой, можно выбрать одно из следующих звеньев: кривошип 1, коромысло 4 и ползун 5. Определим класс механизма для каждого из этих звеньев.
1. Начальное звено – кривошип 1
Разложение начинаем с отделения механизма I-го класса включающего стойку и кривошип 1, связанных вращательной кинематической парой О (рис.1.21,а).
|
Оставшуюся |
кинема- |
|
|
|
5 |
|||
тическую цепь (рис.1.21,б), |
|
|
|
||||||
состоящую из звеньев 2, 3, 4 |
|
|
|
F |
|||||
и 5, нельзя разложить на |
|
|
|
E |
|||||
группы II класса. Действи- |
|
|
|
А |
|||||
тельно, |
при |
отделении |
О |
1 |
|
В |
|||
группы 4-3 остаются два не |
2 |
||||||||
связанных звена 2 и 5, а при |
|
|
|
||||||
|
|
|
|
||||||
отделении |
группы |
5-3 |
|
|
3 |
4 |
|||
остаются |
не |
|
связанные |
|
|
|
|||
|
|
|
С |
D |
|||||
звенья 2 и 4. Следовательно, |
|
|
|
||||||
а) |
|
|
б) |
||||||
оставшаяся |
кинематическая |
|
|
||||||
цепь |
(n 4, |
P5 6) |
будет |
|
|
Рис. 1.21. |
|
||
