4.3.1.Внутренняя норма доходности. Функция чиствндох()43

Внутренняя норма доходности⁴⁴ (internal rate of return - IRR) является наиболее широко используемым критерием эффективности инвестиций.

Под внутренней нормой доходности понимают процентную ставку, при которой чистая современная стоимость инвестиционного проекта равна нулю.

Внутренняя норма доходности определяется путем решения следующе­го уравнения:

( 4‑0)

Нетрудно заметить, что при NPV = 0, современная стоимость проекта (PV) равна по абсолютной величине первоначальным инвестициям I₀, следо­вательно они окупаются. В общем случае, чем выше величина IRR, тем больше эффективность инвестиций. На практике величина IRR сравнивается с заданной нормой дисконта r. При этом если IRR > r, проект обеспечивает положительную NPV, и доходность, равную IRR – r. Если IRR < r, то затраты превышают доходы и проект будет убыточным.

Величина IRR может быть найдена:

• из формулы ЧИСТНЗ() с использование процедуры "Подбор параметра…" (подбирается величина ставки, при которой NPV=0;

• использованием функции ЧИСТВНДОХ()⁴⁵

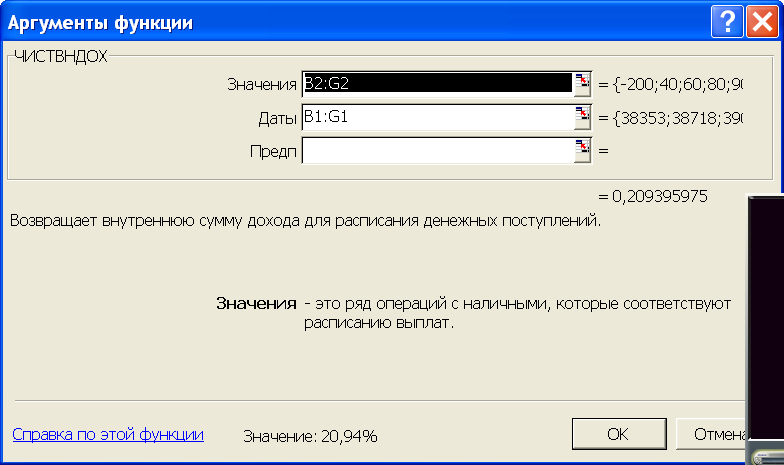
Рис. 4‑60 Диалоговое окно функции ЧИСТВНДОХ()

Пример 4‑58

Фирма намерена 1 января 2005г. инвестировать 200 млн. руб. в проект, ожидаемые доходы по которому в последующие 5 лет составят 40, 60, 80, 90 и 100 млн. руб.

Определите внутреннюю норму дохода по проекту, если поступление доходов будет производится 1 января каждого года

Оцените экономическую эффективность проекта, если рыночная норма дохода составляет 10%

Р ешение

Вариант 1. Использование операции "Подбор параметра…" для определения величины IRR

В ячейках "В3" и "С3" размещается формула вычисления чистого дисконтированного потока =ЧИСТНЗ(10%;B2:G2;B1:G1)т и =ЧИСТНЗ(C4;B2:G2;B1:G1), соответственно

установите курсор в ячейку "С3" и выполните команду СЕРВИС­­_Подбор параметра...;

Рис. 4‑61 Диалоговое окно «Подбор параметра»

в открывшемся диалоговом окне сделайте необходимые установки:

"Установить в ячейке" - $C$3;

"Значение" - 0;

"Изменяя значение ячейки" $C$5.

После щелчка на кнопке "ОК" в ячейку С5 будет возвращено найденное значение IRR =20.94%

Вариант 2. Использование функции ЧИСТВНДОХ()

В ячейку "С6" введите формулу =ЧИСТВНДОХ(B2:G2;B1:G1), возвращающую значение IRR=20,94%

?Таким образом, при рыночной ставке дисконта менее 24% инвестирование проекта – целесообразно.

4.3.2.Модифицированная внутренняя норма доходности. Функция мсвд()

В отличие от NPV, критерий внутренней нормы доходности (IRR) неявно предполагает реинвестирование получаемых доходов по ставке IRR. Если финансирование проекта в рассмотренной выше задаче осуществляется за счет банковской ссуды под 10% годовых, то получаемые в процессе его реализации доходы должны быть реинвестированы по ставке 24,94% годовых, т.е. в 2,5 раза превы­шающей ставку по долгосрочным кредитам! Очевидно, что это вряд ли осу­ществимо в реальной практике.

Для корректного учета предположения о реинвестировании в ППП EXCEL реализована функция МВСД().

Функция МВСД() вычисляет вычислить модифицированную внутреннюю норму доходности (modified internal rate of return - MIRR) при заданной ставке реинвестирования .

Пример 4‑59

Предположим, что в задаче 4.5 имеется возможность реинвестиро­вания получаемых доходов по ставке 8% годовых. Определить модифицированную норму доходности.

Решение

Модифицированная внутренняя норма доходности составит:

=МВСД(B2:G2;10%;8%) =16,02%

Рис. 4‑62 Диалоговое окно функции МСВД (MIRR)

Нетрудно заметить, что полученная модифицированная норма рента­бельности ниже предыдущей, однако выше заданной, поэтому даже при пессимистичной оценке реальных условий проект можно считать прибыльным.