3.3.Расчет периодических платежей
Функции Excel помимо расчета наращенной и приведенной стоимости позволяют выполнить основные расчеты, связанные с оценкой периодических платежей:
Периодические постоянные по величине платежи, осуществляемые на основе постоянной процентной ставки (функция ПЛТ());
Платежи по процентам за конкретный период (функция ПРПЛТ());
Сумму платежей по процентам за несколько периодов, идущих подряд друг за другом (функция ОБЩПЛАТ());
Основные платежи по займу (за вычетом процентов) за конкретный период (функция ОСНПЛАТ());
Сумму основных платежей за несколько периодов, идущих подряд (функция ОБЩДОХОД()).
Наиболее часто все эти величины используются при составлении плана (схемы) равномерного погашения займа. Если заем погашается равными платежами в конце (начале) каждого периода , то будущая стоимость этих платежей ( при его полном погашении) будет равна сумме займа с начисленными процентами к концу последнего расчетного периода. В тоже время текущая стоимость выплат по займу должна быть равна настоящей сумме займа.
Если известна величина займа, срок на который он был выдан и процентная ставка, то можно легко, используя функцию ПЛТ(), определить величину периодических платежей, необходимых для равномерного погашения займа.
Вычисленные платежи включают в себя сумму процентов по непогашенной части займа и основную выплату по нему. Эти величины зависят от номера периода и могут быть рассчитаны с помощью функций ПРПЛТ(), ОСНПЛАТ(). Накопленные суммы могут быть определены с помощью функций ОБЩПЛАТ(), и ОБЩДОХОД().
3.3.1.Определение будущей (наращенной) стоимости потока платежей. Функция бс()
Наращенная
сумма – сумма всех платежей с
начисленными на них процентами к концу
срока ренты. Это может быть обобщенная
сумма задолженности, итоговый объем
инвестиций и т.п.
Рис. 3‑25 Логика финансовой операции наращения финансовой ренты
Методику определения будущей стоимости аннуитета покажем на следующем примере.
Пример 3‑39
На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит владельцу счета.
Решение
FVn=CF*(1+r)n-1+
CF*(1+r)n-2+…+
CF =
( 3‑0)
FV5 =
=4521,55
Таким образом, сумма всех взносов с начисленными процентами будет равна 4521.545 руб.
F
При
использовании финансовых функций Excel
=БС(30%;5;-500;;0)=4521.55
Рис. 3‑26 Решение примера с использованием функции БС()
Как мы уже отмечали ранее, платежи могут осуществляться j-раз в году (ежемесячно, ежеквартально и т.д.). Наиболее распространен случай, когда число платежей в году совпадает с числом начислений процентов, В этом случае общее число платежей за n-лет будет равно m*n, процентная ставка – r/m, а величина платежа – CF/m. Тогда, выполнив преобразования над (5-1), получим:
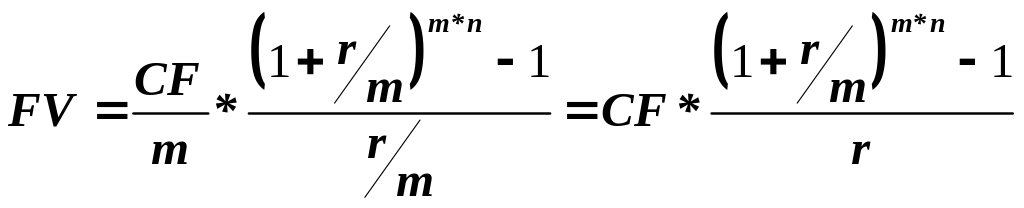( 3‑0)
Пример 3‑40
Предположим, что каждый год ежемесячно в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце каждого месяца. Какова будет величина вклада к концу 4-го года ?
Общее количество платежей за 4 года равно: 4* 12 = 48. Ежемесячная процентная ставка составит: 12% / 12 = 1%.
Решение:
=61222,61
FПри использовании финансовых функций Excel
=БС(12%/12;4*12;-1000)= 61222,61
Рис. 3‑27 Решение примера 3-2