2.2 Реальная динамика тела в среде

При малых значениях скорости сила сопротивления среды пропорциональна скорости, при больших- начинает сильнее зависеть от нее. Восстановление силы сопротивления динамической системы является сложной экспериментальной задачей и, обычно, в моделировании используется степенное разложение при условии, что изменение знака проекции скорости меняет знак проекции силы, т.е. F=Av+B|v|v+Cv³+...

При решении задач предпочтительнее разложение в ряд по нечетным степеням аргумента, для нечетных функций, причем нелинейные задачи, как правило, не имеют аналитичес­кого решения. Заметим, что в широком диапазоне чисел Рейнольдса ~10²- 10⁶ сила сопротивления является квадратичной функцией скорости . Здесь С~0.5 для шара, - плотность среды, S- площадь поперечного сечения тела.

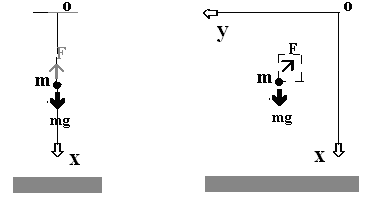
(а) (б)

Рис.2. Динамика тела с учетом сопротивления среды

Рассмотрим простой одномерный случай падения тела в вязкой среде вдоль оси X, без начальной скорости (рис. 2 а). Начало координат поместим в точку О, из которой начинается движение тела. На тело действуют две силы: сила тяжести mg и сила сопротивления воздуха F=-kv.

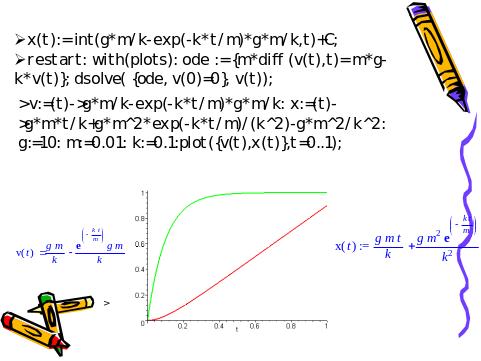
Слайд 8. Динамический метод на компьютере

По второму закону Ньютона имеем дифферен­циальное уравнение для неизвестной функции скорости v(t): . Разделяя переменные, находим , или . Далее, после интегрирования получаем: . Произвольную постоянную С определяем из на­чальных условий v(0)=0: C = Ln(mg/k). После несложных преобразований на­ходим закон изменения скорости тела: . Из полученного решения видно, с ростом времени t скорость стремится к своему максимальному значению , т.е. установившее­ся движение тела в вязкой среде является равномерным.

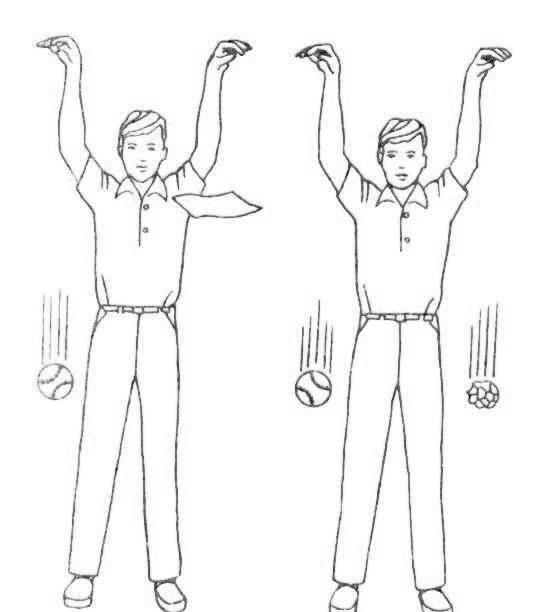
Рис.3. Демонстрационный эксперимент в физике

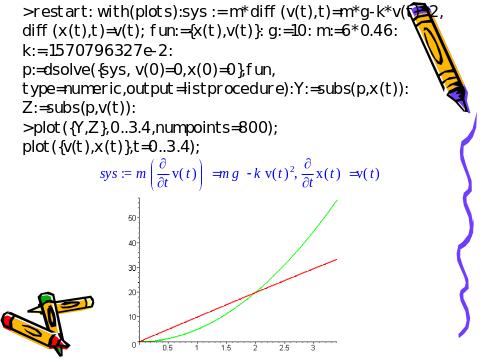
Слайд 9. Численное моделирование методом Рунге-Кутты 4-го порядка точности

Так как закон изменения скорости известен, то, решая обратную задачу кине­матики , можно найти закон движения x(t) по заданному началь­ному условию x(0)=0.

Решение задачи для квадратичной силы сопротивления приводится в учебном пособии [19]. Дифференциальное уравнение движения имеет вид:

. Решение представлено уравнениями:

Интегрирование гиперболических функций в формулах представляет трудности для компьютера, поэтому воспользуемся численными методами (слайд 9).

2.3 Цепная линия и метод кратных скобок Пуассона

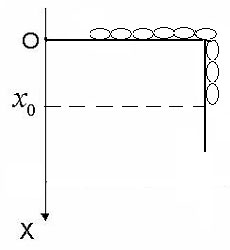
Рассмотрим задачу. Однородная цепочка длиной l свисает на величину x₀ c края горизонтального стола, по которому она может скользить без трения. Найти зависимость x(t), если v₀=0.

Эта задача имеет точное решение. Уравнение движения цепочки записывается в виде:

Решение уравнения при x>l соответствует равноускоренному дви-жению:

,

где t  момент времени, в который вся цепочка принимает вертикальное положение, а v_{1 } ее скорость в этот момент времени.

Далее удобно ввести . Общее решение уравнения движения при записывается в виде:

.

При заданном начальном условии решение принимает вид: где момент времени t₁ определяется соотношением , а значение v₁ определяется следующим образом:

.

Интересно сопоставить это решение с решением, получаемым методом кратных скобок Пуассона в теоретической физике [7].

Записав функцию Гамильтона в виде:

и т. д.

Рис.4. К определению гиперболических функций

В результате получим разложение:

,

которое соответствует общему выражению при произвольных начальных условиях: .

Тогда

.

В частности, при заданных в условии задачи начальных условиях данное разложение сводится к известному выражению для гиперболического косинуса (цепной линии) .

Данная задача особенно ценна для студентов, ибо подобная задача в более простой постановке, когда требуется определить скорость цепочки как функцию длины ее свисающего конца, традиционно предлагается на занятиях по физике в средней школе. Заметим, что процедура вычисления и суммирования кратных скобок Пуассона может быть автоматизирована в среде символьной математики [7].