3.6 Хаотическое поведение маятника и отображение Пуанкаре

Фазовая плоскость определяется как множество точек (x,v). (Иногда вместо скорости v используется импульс p=mv). Когда движение периодично его орбита описывает в фазовой плоскости замкнутую кривую. Вынужденные колебания нели­нейной системы с кубичным упругим элементом могут иметь орбиту с самопересечениями, но, тем не менее, замкнутую. В этом случае следует ожидать присут­ствие субгармоник.

Напротив, орбиты хаотических движений никогда не бывают замкнутыми, не повторяются. Такие орбиты стремятся заполнить некоторую область фазового пространства. Хотя подобное блуждание орбит указывает на хаос, непрерывные графики на фазовой плоскости мало информативны, и следует использовать более совершенный метод исследования фазовых портретов, называемый отображени­ем Пуанкаре.

При математическом исследовании динамических систем отображением на­зывают временную выборку данных , для которой вводят обоз­начение Понятие отображения переносится и на боль-шее число переменных. В простом детерминированном случае отображение представляет систему разностных уравнений. Если и , то эта последова­тельность точек фазового пространства представляет собой двухмерное отобра­жение:

.

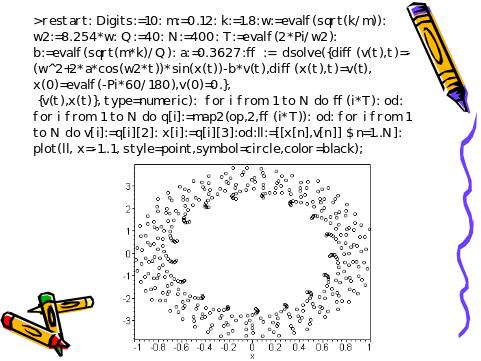
Слайд 18. Отображение Пуанкаре в нелинейной динамике

Если моменты выборки подчиняются определенному правилу, например, кратны характерному периоду системы, это отображение называется отображением Пуанкаре [45].

Для многих механических систем характер движения можно определить приблизительно, комбинируя аналитические и численные методы. При определенных условиях детерминированные системы проявляют хаотическое поведение, чувствительное к начальным данным и к приближениям, сделанным в ходе вычисления траектории. В данном случае мы не в состоянии предсказать долговременное поведение динамической системы.

Указание. Исследовать поведение нелинейного маятника на фазовой плоскости с вертикально осциллирующей точкой подвеса. Уравнение движения имеет вид (Маклафлин, Персиваль, Ричардс (1981 г.):

.

3.7 Циклоидальный маятник

Обратимся к задаче, решение которой позволило нидерландскому ученому Х. Гюйгенсу сконструировать в 1673 г. «точные» часы. Эта задача заключается в построении в вертикальной плоскости такой кривой, чтобы время, необходимое для спуска по ней до фиксированного горизон

та материальной точки, находящейся в начальный момент времени в состоянии покоя, не зависело от исходного положения точки на этой кривой. Как показал Гюйгенс, такой изохронной кривой оказалась циклоида: [3].

Циклоида обладает многими интересными свойствами (например, длина арки циклоиды выражается через диаметр целым числом 4), имеющими исключительное значение для физики и техники. В частности, профили зубьев шестерен, очертания многих типов эксцентриков, кулачков и иных деталей машин имеют форму именно циклоиды.

Р ис.24. Изохронные колебания циклоидального маятника

Практически решение этой задачи можно провести, используя парамет-рические уравнения циклоиды: .

Пусть координаты исходного положения шарика, т.е. точки М, а соответствующее ей значение параметра (рис.24).

Когда шарик скатится из положения М в некоторое положение , он снизится по вертикали на расстояние h, которое определится следующим образом: и, соответственно, скорость тела . С другой стороны, и для циклоиды , и поэтому дифференциальное уравнение принимает вид: .

Слайд 19. Колебания на циклоиде

Интегрируя это уравнение в соответствующих пределах, получаем, что . Если не учитывать трение, то из закона сохранения энергии шарик будет совершать колебания с периодом . Отличительным свойством циклоидального маятника по сравнению с обычным (круговым) является то, что период его колебаний не зависит от амплитуды (изохронные колебания).

При малых колебаниях контур циклоиды можно считать круговым и, положив L= 4r, получаем период малых колебаний математического маятника .