4.1 Нормальное распределение и статистический критерий

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в науке и занимает среди других законов распределения особое положение. Это- наиболее часто встречающийся в теории и практике закон распреде­ления, например, в оптике или атомной спектроскопии (рис.33, 34). Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Отметим, что расширенные средства графики распространенных математических пакетов обеспечивают наглядность при изучении вероятностно- статистических моделей и методов с помощью компьютера.

Рис. 33. Иллюстрация гауссова пучка в оптике

Согласно центральной предельной теореме сумма достаточно большого числа незави­симых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному за­кону, и это выполняется тем точнее, чем большее количество слу­чайных величин суммируется.

Большинство встречающихся на прак­тике случайных величин, таких, например, как ошибки физических измерений, могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых- элементарных оши­бок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.

Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономер­ностей, фактически существующих в массовых случайных явлениях природы.

Оперируя такими понятиями, как события и их вероят­ности, случайные величины, их законы распределения и числовые характеристики, теория вероятностей дает возможность теоретиче­ским путем определять вероятности одних событий через вероятности других, законы распределения и числовые характеристики одних случайных величин через законы распределения и числовые характе­ристики других. Такие косвенные методы позволяют значительно экономить время и средства, затрачиваемые на эксперимент, но отнюдь не исключают самого эксперимента. Каждое исследование в области случайных явлений, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений.

Разработка методов регистрации, описания и анализа статисти­ческих экспериментальных данных, получаемых в результате наблю­дения массовых случайных явлений, составляет предмет специальной науки- математической статистики. Все задачи математической статистики касаются вопросов обра­ботки наблюдений над массовыми случайными явлениями, но в зави­симости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут прини­мать ту или иную форму.

Закономерности, наблюдаемые в массо­вых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин.

Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с огра­ниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат боль­ший или меньший элемент случайности.

Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и про­являются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обра­ботки экспериментальных данных следует предъявить такие требо­вания, чтобы она, по возможности сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного мате­риала. В связи с этим возникаем характерная для математической статистики задача сглаживания или выравнивания стати­стических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.

Рис. 34. Модель доплеровского уширения спектральных линий атомов

Если говорить о статистической проверке статистических гипотез, то наиболее распространенным критерием является критерий К. Пирсона.

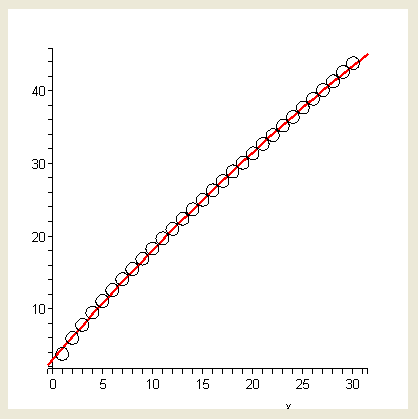
Рис. 35. Интерактивная аппроксимация критических точек - распределения в среде Maple 9.5

Для распределения составлены специальные таблицы (сумма по числу частных интервалов гистограммы измерений (рис. 36). Пользуясь этими таблицами, можно для каждого зна­чения числа степеней свободы r найти вероятность р того, что величина, распределенная по закону превзойдет это значение. В таблице входными данными являются значение вероятности р и число степе­ней свободы r. Числа, стоящие в таблице, представляют собой соот­ветствую-щие значения .

Распределение дает возможность оценить степень согласованности теоретического и статистического распределений. Будем исхо­дить из того, что величина X действительно распределена по закону F(x).

Тогда вероятность p определенная по таблице, есть вероятность того, что за счет чисто случайных причин мера расхож­дения теоретического и статистического распределений будет не меньше, чем фактически наблюдаемое в данной серии опытов значений . Если эта вероятность весьма мала настолько, что событие с такой вероятностью можно считать практически невозможным, то результат опыта следует считать противоречащим гипотезе Н о том, что закон распределения величины X есть F(x). Эту гипотезу следует отбросить как неправдоподобную.

Напротив, если вероятность р сравнительно велика, можно признать расхождения меж­ду теоретическим и статистическим распределениями несущественными и отнести их за счет случайных причин. Гипотезу Н о том, что величина X распределена по закону F(x) можно считать правдо­подобной или, по крайней мере, не противоречащей опытным данным [1].

В учебной литературе, например, в учебниках [10, 17] дается разная интерпретация данного статистического критерия. В методике учебного физического эксперимента представляет интерес компьютерный вариант реализации критерия согласия теории c опытными данными без использования специальных таблиц и терминов, с помощью универсальной программы. Заметим, что критерий представленный в [10] для программирования предпочтительнее; он не требует дополнительной аппроксимации таблично заданных функций (рис. 35).

Зная плотность распределения - , где Г(r/2)- гамма- функция, искомую вероятность критерия находим интегрированием (рис. 36). Отметим аналитические возможности системы символьной математики Maple, позволяющие вычислить интеграл в явном виде:

, где - Whittaker- функция. К сожалению, полученная формула применима не при всех значениях , представляющих практический интерес.

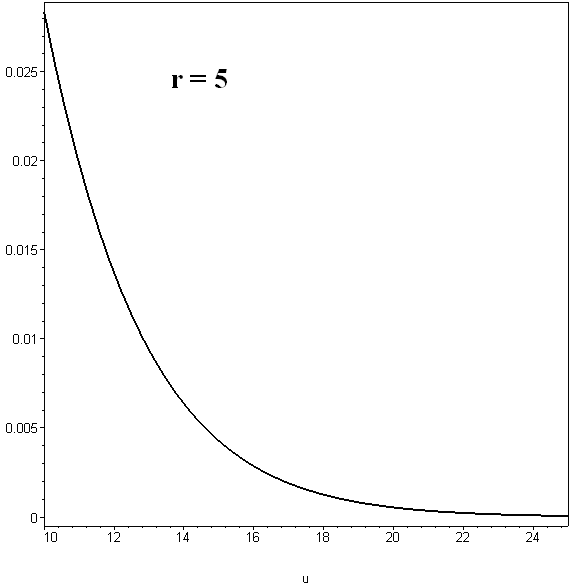
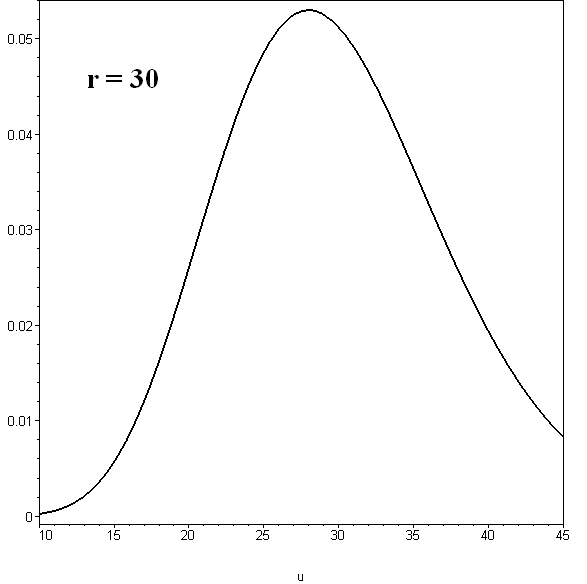
Рис.36. Плотность распределения в проверке статистических гипотез