3.8 Задача с соударениями

Рассматриваются упругие соударения шарика с равномерно движущейся стенкой. Шарик упруго отскакивает между двумя стенками. В случае неподвижных стенок скорость при отскоке будет одинаковая. Если одна из стенок движется, то скорость шарика после отскока от нее будет изменяться, в зависимости от направления движения стенки. При сближении стенок расстояние между ними уменьшается, скорость отскока- увеличивается, а произведение I=Lv – практически cохраняется (с точностью до 0,5%), т.е. I = inv.

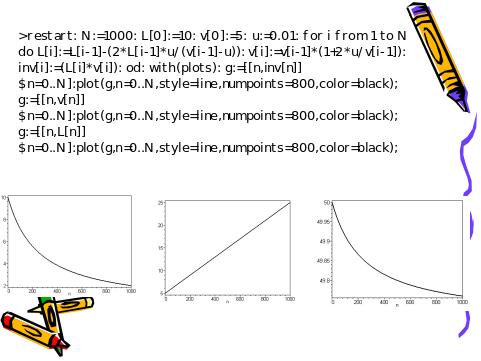
Слайд 20. Иллюстрация точности адиабатического инварианта

Указание. В программу включить цикл по числу соударений i=1...N для следующей системы уравнений:

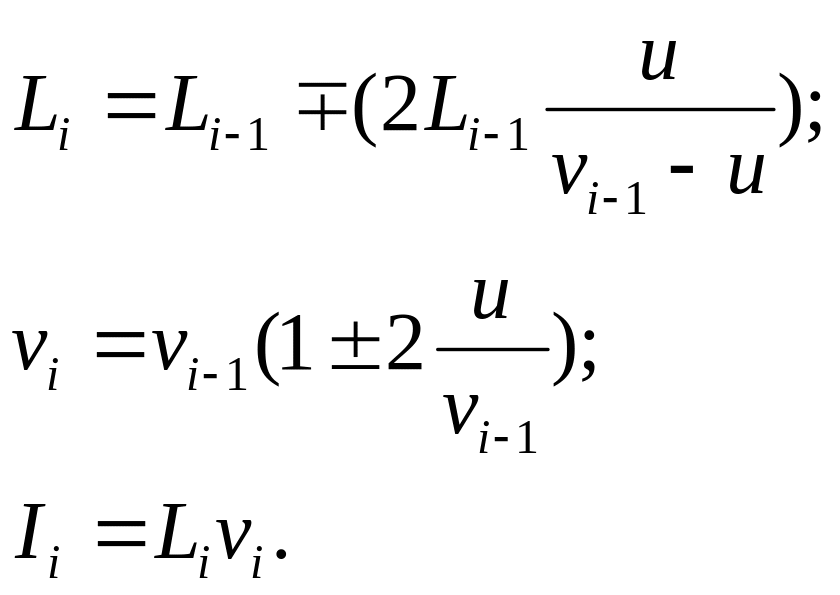
Знак в уравнениях зависит от направления движения стенки, причем, U<<V. Параметры задачи: N=1000, L_o =10 м, V_o =5 м/с, U=0.01 м/с .

3.9 Хаотические колебания при соударениях

Рассматривается нелинейная математическая модель, в которой шарик подскакивает на колеблющейся опоре (модель ускорения частиц в электромагнитном поле). Сделав некоторое предположение о потерях энергии при каждом соударении, мож­но получить следующие разностные уравнения (двумерное отображение):

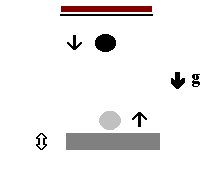
Рис.25. Модель Ферми ускорения космических лучей

Здесь ф- фаза опоры в момент соударения, v- безразмерная скорость после соударения, к- поте­ри энергии при соударении, величина А пропорциональна амплитуде колеблющейся опоры [45].

Случай консервативного хаоса исследован Лихтенбергом и Либер-маном как модель ускорения электронов в электромаг­нитных полях. По решениям системы уравнений временной контур координаты гравитирующей массы восстанавливается по законам кинематики. В эксперименте необходимо варьировать начальные условия.

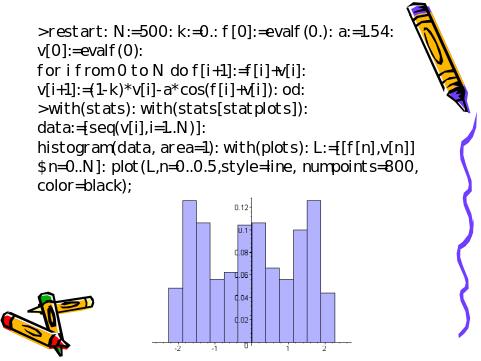
Слайд 21. Гистограмма измерений в динамике хаотических колебаний

3.10 Представление колебаний рядом Фурье

Рассматриваются колебания шарика при упругих отскоках от неподвижной опоры (слайд 22).

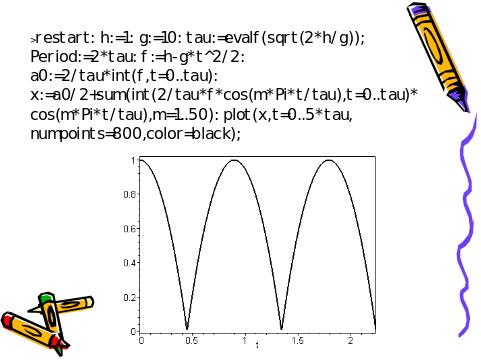
Слайд 22. Разложение периодической функции в ряд Фурье

Указание. Определите период колебаний по формулам кинематики и постройте график координаты от времени, используя разложение функции в ряд Фурье. Данные ввести самостоятельно.

3.11 Два тела на пружине

Решение в общем виде допускает задача о движении системы, состоящей из двух взаимодействующих частиц. Рассмотрим наиболее простую систему двух тел (материальных точек) соединенных легкой пружиной.

В качестве предварительного шага к решению этой задачи покажем, каким образом она может быть упрощена путем рассмотрения движения системы частиц относительно центра масс с учетом обобщенного принципа инерции. Другими словами задачу двух тел можно свести к задаче движения одного тела приведенной массы в потенциальном поле.

Потенциальная энергия взаимодействия двух частиц зависит лишь от расстояния между ними. Поэтому функция Лагранжа системы имеет вид .

Введем расстояние между точками и поместим начало координат в центре масс, что дает . Из двух последних равенств находим: ; . Нетрудно видеть, что функция Лагранжа , где , - приведенная масса.

Функция L формально совпадает с функцией Лагранжа одной материальной точки с приведенной массой m, движущейся в потенциальном поле, в нашем случае, , симметричном относительно неподвижного начала координат. Поэтому собственная частота колебаний материальных точек определяется по известной формуле пружинного маятника .

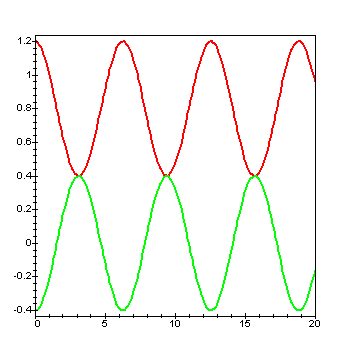
Рис.26. Колебания в формализме Лагранжа

Неизменность законов механики по отношению к линейным преобразованиям координат и времени в ИСО предполагает неизменность вида функций от координат, скоростей и ускорений, фигурирующих в уравнениях, т.е. инвариантность к заданному преобразованию, например, к сдвигу координаты (однородность пространства). Такие уравнения называются ковариантными относительно группы преобразований. Примером может служить система динамических уравнений в рассматриваемой задаче двух тел на основе дифференциальных законов Ньютона: , где L- длина ненагруженной пружины. Результат численного интегрирования системы уравнений для равных масс на компьютере приведен на рис. 26. Заметим, что при более сложных преобразованиях исходной системы отсчета, например, при переходе к полярным координатам ковариантность уравнений движения в форме Ньютона утрачивается.

Указание. Провести вычислительный эксперимент при разных параметрах и начальных условиях. Проверить теорему о движении центра масс.