4.12 Модели плоских фигур

Вычислить массу, центр масс, момент инерции диска с заданной плотностью. Данные ввести самостоятельно.

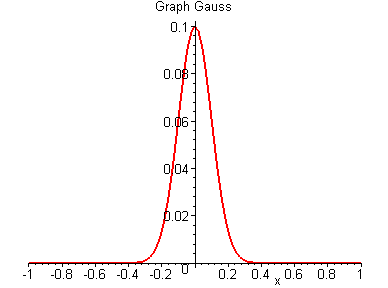
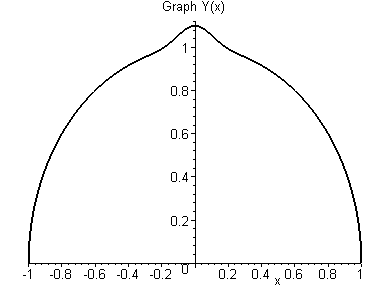
Рис.48. Вычисление площади круга с малым возмущением

Слайд 29. Оценка точности метода Монте-Карло для площади круга

4.13 Площадь круга с малым возмущением

Для оценки точности и чувствительности метода Монте-Карло в задачах интегрирования внесем в круг малое гауссово возмущение с помощью функции Хевисайда (единичной ступени):

(рис. 48 , слайд 29).

Указание. Вычислить площадь круга с малым возмущением. Данные ввести самостоятельно.

4.14 «Игла Бюффона»

Требуется найти длину «иглы» многократным случайным подбрасыванием. В другой формулировке задачи при известной длине «иглы» определяем число . [32]

Будем бросать «иглу» на параллельные линии ширины 2a>2L, где L- длина иглы. Причем, положении «иглы» определим двумя случайными величинами ; х- расстояние от центра «иглы» до ближайшей линии, - угол наклона (рис. 49 а).

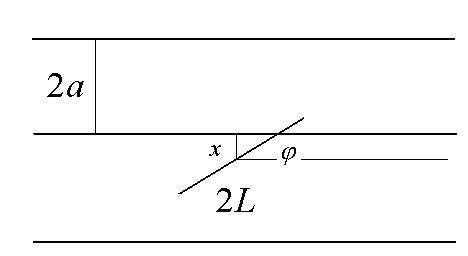
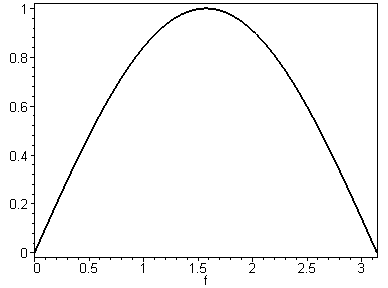
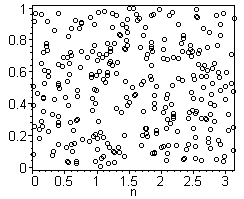
а) б) в)

Рис.49. Геометрия задачи «Игла Бюффона»

Указание. Задача обсуждается в журнале [32]. Определите число с помощью «иглы» Бюффона» генерируя случайные числа на плоскости ( ,х) при a=L=1 (рис. 49 в). Оцените точность, время счета и оптимальное число бросков (испытаний) для минимальной погрешности.

Слайд 30. Определение числа с помощью «иглы Бюффона»

Из геометрии задачи следует условие попадания на линию . Заметим, что геометрическая вероятность определяется отношением площадей (рис. 49 б).

Учитывая, что , находим число , где m- число попаданий на линию (под график синуса), n- общее число случайных бросков.

4.15 Выделение сигнала на фоне «шумов»

Зададим некоторый двухчастотный сигнал, имеющий, например, 2¹⁰=1024 точек отсчета. Далее, с помощью генератора случайных чисел с нормальным распределением (математической модели реальных физических помех) наложим на полезный сигнал «шум» (рис. 50).

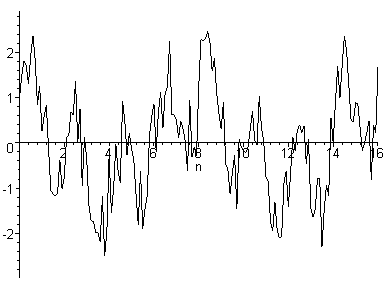
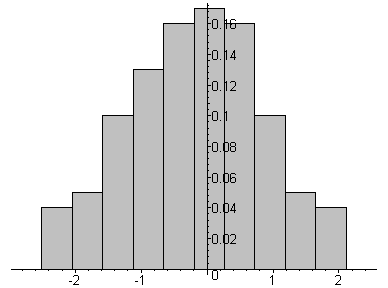
Рис. 50. Математическая модель реального сигнала с нормально-распределенным «шумом»

Нетрудно заметить, что теперь форма сигнала замаскирована «шу-мом» и можно лишь с трудом догадываться, что сигнал имеет периодические составляющие.

Выполнив операции вычисления амплитудного спектра, восстановим полезный сигнал с двумя гармониками:

(рис. 51).

Указание. Используйте программу быстрого преобразования Фурье FFT из математического пакета Maple [20].

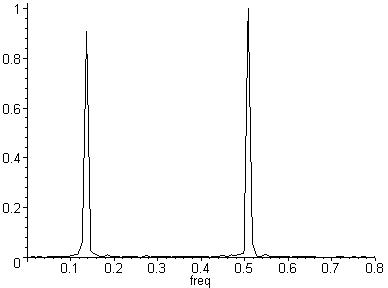
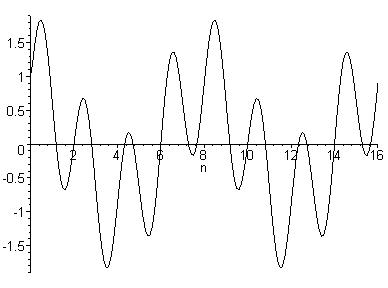
Рис. 51. Спектральный анализ сигнала на ПК

Слайд 31. Выделение колебаний на фоне «шумов»

4.16 Регрессионная модель эксперимента и метод наименьших квадратов

Переходя от реальных экспериментальных условий к математическому описанию можно говорить о математической модели эксперимента.

С появлением ПК возникла методология имитационного моделирования, направленная не на изучение природы, а на изучение достаточно сложной имитационной модели. Такая модель часто требует имитации случайности и широкий класс имитационных экспериментов укладывается в схему получения реализаций случайной функции при заданной выборке измерений.

В связи с планированием принято выделять следующие типы эксперимента. Экстремальный эксперимент, задача которого состоит в определении экстремальных значений функции регрессии. Эксперимент по проверке конкретной статистической гипотезы (дискриминирующий эксперимент). Отсеивающий эксперимент, задача которого состоит в выделении значимых факторов. Компьютерный имитационный эксперимент связан с имитацией изучаемого явления на компьютере, позволяющей воспроизводить измерения с приемлемой точностью.

Специфической задачей теории планирования эксперимента является конструирование критерия его оптимальности с учетом априорной информации, находящей свое отражение в гипотезе модели изучаемого явления, например, в рамках регрессионного анализа с методом наименьших квадратов.

Первая работа, в которой использовался метод наименьших квадратов (МНК), принадлежит Лежандру («Новые методы определения орбит комет», 1805 г.). В работе Р.Адрейна «Исследования, касающиеся вероятностей ошибок, которые появляются при измерениях» (1808 г.) показано, что при нормальном распределении ошибок метод наименьших квадратов дает наиболее правдоподобное решение для неизвестных параметров некоторой линейной формы. В 1809 г. Гаусс дал второе обоснование нормального распределения ошибок. Кроме того, он отста-ивал приоритет МНК с 1795 г. Начиная с 1810 г. метод наименьших квадратов использовали Лаплас, Бессель и позже Энке. В 1831 г. Коши предложил другой критерий минимакса.

Дальнейшее развитие метода связано с именем Лапласа, который в 1812 г. в работе «Аналитическая теория вероятностей», доказал, что этот метод позволяет найти несмещенные оценки безотносительно к типу исходного распределения. Гаусс опубликовал свои соображения в 1821 г. о несмещенных оценках параметров и независимости от типа распределения. В более общем виде эта теорема была доказана в 1912 г. А.Марковым и известна как теорема Гаусса-Маркова. Заметный вклад в развитие метода был внесен в 1934 г. Эйткеным, который обобщил теорему на случай коррелированных результатов наблюдений с различными дисперсиями [58].

Стандартный метод оценки линии регрессии основан на использовании линейной относительно параметров модели:

в схеме Гаусса-Маркова Причем, для полиномиальной зависимости матрица системы нормальных уравнений и ковариационная матрица (матрица ошибок) приводятся в книге [58]: . В книге Дерека Худсона рассматривается пример математической модели реальных измерений с нормально- распределенной ошибкой (нормальный регрессионный анализ). К значениям параболической функции были добавлены случайные ошибки с единичной дисперсией.

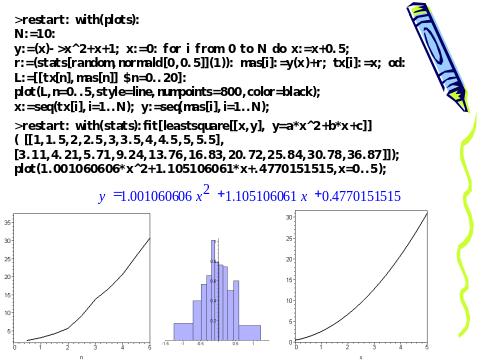
Слайд 32. Нормальный регрессионный анализ в программе Maple

В методическом аспекте заметим, что стандартные функции математических пакетов, обычно, не вычисляют ковариационные матрицы с дисперсиями искомых параметров (линейной несмещенной оценки МНК). Поэтому учебные компьютерные регрессионные модели целесообразны в плане развития исследовательской культуры.

Указание. Сформулируйте и решите задачу линейной регрессии. Оцените погрешность искомых параметров. Данные ввести самостоятельно.