4.5 Статистическое распределение с бесконечной дисперсией

Рассмотрим следующую задачу. Фонарь установлен на единичном расстоянии от длинной стены и случайным образом мерцает. Найти плотность распределения светлых пятен на стене при равномерном вращении источника света вокруг вертикальной оси.

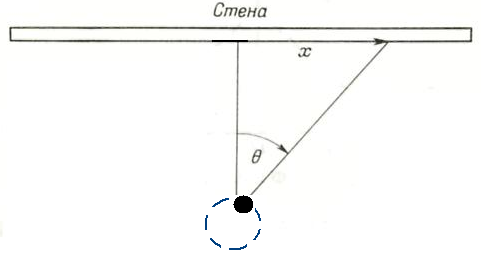
Рис. 37. Иллюстрация задачи, приводящей к бесконечной дисперсии

В силу того, что все значения углов падения лучей равновероятны, для случайного угла имеем равномерное распределение на интервале от до : . Поскольку , то . Таким образом, плотность распределения случайной координаты светлого пятна на стене выражается функцией . Это экзотическое распределение Коши имеет бесконечную дисперсию. В этом легко убедиться с помощью расчетов на компьютере.

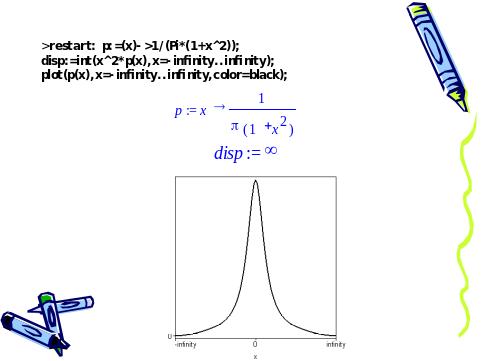
Слайд 26. Статистическое распределение с бесконечной дисперсией

4.6 Закон больших чисел и центральная предельная теорема

Как известно, в эксперименте нельзя заранее уверенно пред­видеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих слу­чайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы распо­лагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. Но, оказывается, что при некото­рых сравнительно широких условиях суммарное поведе­ние достаточно большого числа случайных величин почти утрачивает случайный характер и становится законо­мерным.

Для практики очень важно знание условий, при вы­полнении которых совокупное действие очень многих слу­чайных причин приводит к результату, почти не завися­щему от случая, так как позволяет предвидеть ход явле­ний. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим [1].

Сущность теоремы Чебышева состоит в том, что хотя от­дельные независимые случайные величины могут прини­мать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случай­ных величин с большой вероятностью принимает значе­ния, близкие к определенному постоянному числу, а именно к математическому ожиданию. Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных вели­чин, но можно предвидеть, какое значение примет их среднее арифметическое. Теорема Чебышева справедлива не только для дискрет­ных, но и для непрерывных случайных величин.

Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифме­тическое принимают в качестве искомого.

К физическим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же ма­тематичес-кое ожидание, 3) дисперсии их равномерно огра­ничены.

Первое требование выполняется, если результат каж­дого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произ­ведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы. Третье требо­вание выполняется, если прибор обеспечивает определен­ную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено.

Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства . Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отли­чается от истинного значения измеряемой величины.

Итак, теорема Чебышева указывает условия, при ко­торых описанный способ измерения может быть приме­нен. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точ­ности. Дело в том, что сам прибор (методика эксперимента) дает показания с конечной точностью ограничивающей точность эксперимента.

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положитель­ный ответ на этот вопрос дает теорема, доказанная Яко­бом Бернулли (опубликована в 1713 г.), которая полу­чила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л.Чебышевым в 1846 г. Итак, теорема Бернулли утверждает, что сходится по вероятности при . Другими словами, например, можно предсказать относительную частоту падение тела в заданную точку при случайных порывах ветра обобщая решения типовых физических задач.

Известно, что нормально распределенные физические величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдаю­щимся русским математиком А.М.Ляпуно-вым (централь­ная предельная теорема): если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

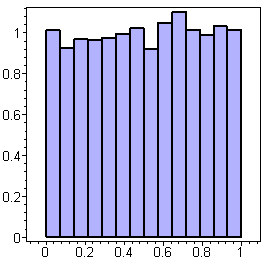
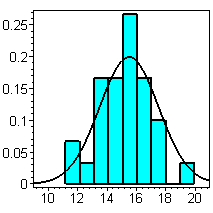
Рис. 38. Иллюстрация вероятностных теорем на компьютере

В частности, если все случайные величины одинаково распределены, то к этой последовательности применима центральная предельная Теорема, если диспер­сии всех величии конечны и отличны от нуля. А. М. Ляпунов доказал, что если для при отношение Ляпунова , где стремится к нулю (условие Ляпунова), то к последова­тельности применима центральная предельная теорема.

Для иллюстрации вероятностных теорем воспользуемся компьютерным генератором случайных чисел и наглядной графикой, которая дает представление о законах распределения случайных измерений, гистограмме, о правиле «трех сигм» для нормального распределения (рис. 38).