1.4 Сопротивление бесконечной электрической цепи

В силу симметрии добавление или исключение звена в бесконечной цепочке сопротивлений не меняет общего сопротивления цепи:

. Решая квадратное уравнение для , получаем (рис.1) [9].

Рис.1. Физическая симметрия в задаче о сопротивлении

электрической цепи

1.5 Сопротивление конечной электрической цепи

Сопротивление цепочки из n звеньев выражается рекуррентной формулой 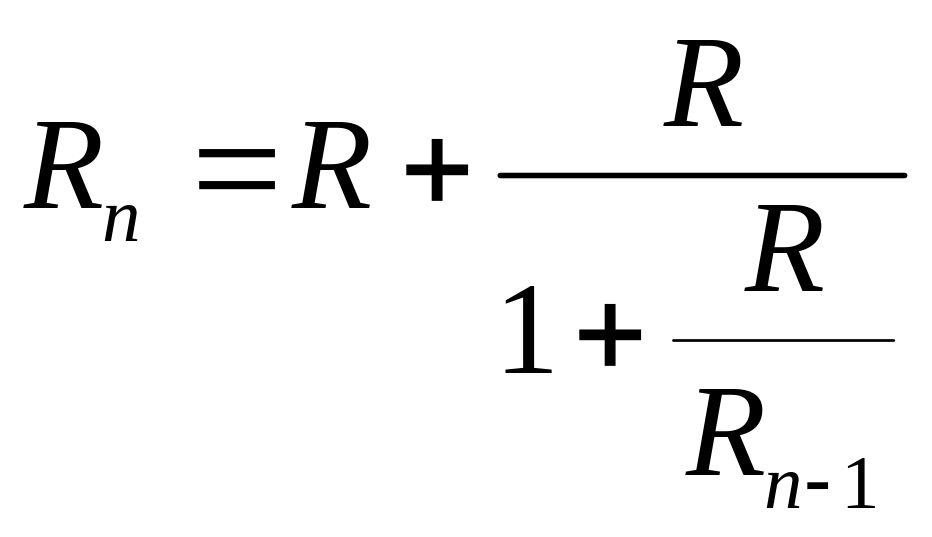, R₁=2R. (cлайд 4)

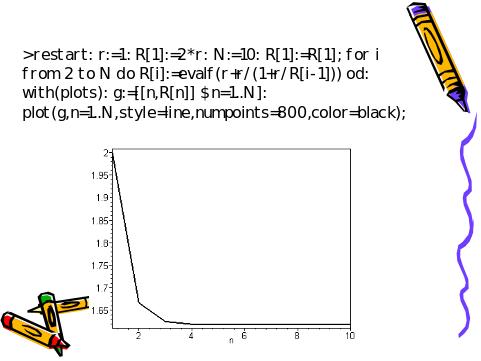
Слайд 4. Сопротивление конечной электрической цепи

1.6 «Золотое сечение» в поле тяготения

Известно, что ускорение силы тяжести при удалении от земной поверхности описывается следующей формулой (докажите!):

,

где h- высота над поверхностью Земли, R- ее радиус. При опускании тела в глубь Земли характер зависимости g от расстояния меняется:

.

Зададимся вопросом, когда . Ясно, что одним из решений будет [26]. Второе реше­ние (которое мы можем найти на компьютере, написав строчку Maple- программы):

(слайд 5).

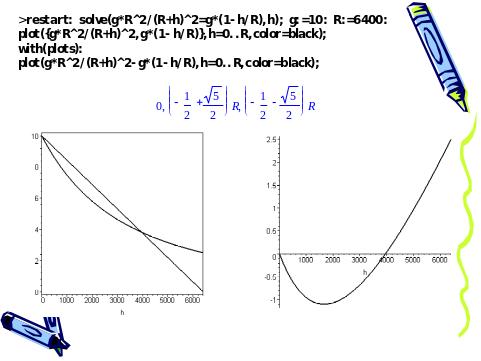
Слайд 5. Графический метод в физике

Указание. Решить уравнения графическим методом [25]:

2. Динамическое моделирование и вычислительный эксперимент

В соответствии со вторым законом Ньютона дифференциальное уравнение движения: . Сумма проекций сил в правой части может быть постоянной, а мо­жет зависеть от координаты, скорости, времени, параметров. Это дифференциаль­ное уравнение, которое аналитически легко решается только в простейших слу­чаях. Численный приближенный метод основан на замене дифферен­циальных уравнений конечно-раз-ностными алгебраическими уравнениями с заданной точностью. Наиболее распространенными до сих пор являются методы Рунге-Кутты реализованные в стандартных процедурах современных математических пакетов.

В 1885 г. К. Рунге высказал основную идею метода численного ре-шения систем дифференциальных уравнений, которую в 1901 г. развил и усовершенствовал В. Кутта. На этой основе была разработана серия вычислительных методов различной степени точности, ориентированных на случай дифференциальных систем [47].

Следует обратить внимание на то, что, в зависимости от содержания, задачи могут решаться в разных системах единиц, а также в безразмерных величинах.

1. Равенство тяжелой и инертной массы в свободном падении

Масса является физической величиной, характеризующая взаимодействие тел, определяет инертные и гравитационные свойства. Под инертностью материальных тел понимается их способность сохранять состояние покоя или равномерного и прямолинейного движения. Инерт-ная масса является мерой этой способности, т.е. мерой инертности тела. Она определяется как коэффициент пропорциональности между силой и ускорением в уравнении движения классической механики: . Инертная масса является также коэффициентом пропорциональности между импульсом (количеством движения) тела и его скоростью: .

Под гравитационным свойством материальных тел понимается их способность создавать в окружающем пространстве гравитационное по­ле и испытывать воздействие полей тяготения, создаваемых другими материальными телами. В этом отношении они аналогичны электрически заряженным телам, создающим вокруг себя электрическое поле и ис­пытывающим воздействие электрических полей, создаваемых другими за­ряженными телами. Гравитационная масса выступает как гравитационный заряд. Согласно закону всемирного тяготения сила гравитационного взаимодействия точечных тел пропорциональна произведению их гравитационных масс m₁^(g) и m₂^(g) и обратно пропорциональна квадрату расстояния между ними .

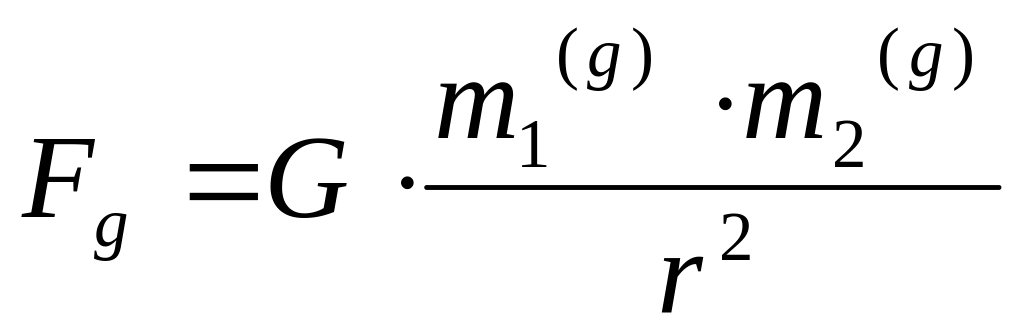Инерция тел и их способность возбуждать в окружающем простран­стве гравитационные поля не могут априори (до опыта) рассматри­ваться как взаимосвязанные и тем более тождественные свойства тел. Поэтому возникает вопрос, какова взаимосвязь между инертной и гравитационной массами тел? Равны эти массы или пропорциональны друг к другу- эти утверждения не из каких теоретических положений механики не вытекают. Этот вопрос может быть решен только опытным путем.

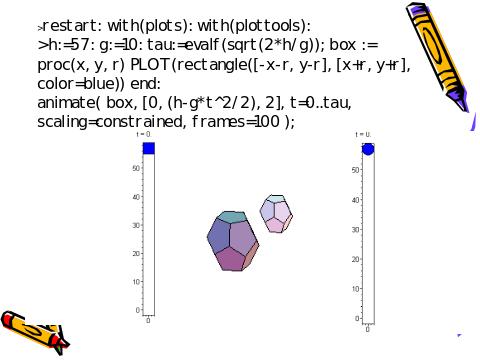
Слайд 6. Визуальное моделирование

свободного падения с графическими примитивами

Слайд 7. Pascal- программа измерения ускорения свободного падения

Рассмотрим свободное падение тел в однородном поле тяготения Земли. Так как тела падают под действием силы тяжести, то по второму закону Ньютона m⁽ⁱ⁾a=m^(g)g. Тогда ускорение, с которым тела падают на Землю: .

Опытным путем можно установить закон, согласно которому все тела свободно падают на Землю с одинаковым ускорением а, равным g=9,8 м/с², из чего следует, что инертная и гравитационная массы равны. Кроме того, используя компьютер можно измерить время и ускорение свободного падения, а также проиллюстрировать исторический закон нечетных чисел Галилея.