5.5 «Перевернутая» игра Баше

На столе лежат n монет. Два игрока по очереди берут со стола от 1 до К монет. Проигравшим считается тот, кто возьмет последние монеты.

Указание: Выигрышная стратегия игры приводится в журнале [23]. Количество оставляемых монет должно при делении на 4 давать остаток 1. Составить программу игры на алгоритмическом языке высокого уровня.

5.6 Игра в 15

В плоской квадратной коробочке лежат 15 шашек с номерами. «Нор­мальное» расположение шашек пока­зано на рис. 56, а также по­казано другое расположение; шашки с номерами 14 и 15 переставлены. Нужно, передвигая по очереди по одной шашке, перевести это располо­жение в «нормальное». Шашки пе­редвигают на свободное соседнее ме­сто, вынимать их из коробочки не разрешается.

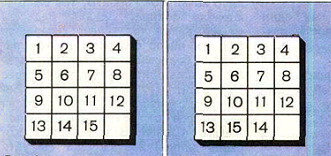
Рис.56. Игра в 15

Игру в 15 изобрел в семидесятых годах XIX века Сэм Лойд. По­вальное увлечение игрою быстро охватило Англию, а потом перекинулось и через Ла-Манш. Свой рассказ об этом Мартин Гарднер иллюстрирует цитатой из самого Лойда: «Люди буквально помешались на этой головоломке. Из уст в уста пере­давались рассказы о лавочнике, за­быв-шем открыть свою лавку, о свя­щеннике, простоявшем под уличным фонарем долгую зимнюю ночь в на­дежде припомнить, как ему удалось решить задачу... Один известный редактор из Бал­тимора рассказывает, что один раз он ушел в полдень на ленч и лишь поздней ночью был обнаружен вко­нец отчаявшимися сотрудниками га­зеты сидящим за столом и гоняющим взад- вперед по тарелке маленькие кусочки пирога!» [30]

Указание. Математическая теория игры разбирается в журнале [31].

Разработать программу игры в 15 на алгоритмическом языке высокого уровня.

5.7 Игра «Покер»

Диалоговый режим работы на ПК при использовании языка программирования высокого уровня позволяет реализовать игровые программы, в которых компьютер генерирует случайные числа, необходимые практически в любой игре.

В описываемой игре «Покер» используется пять кубиков (костей) с пронумерованными от 1 до 6 гранями.

Естественно, что при бросании кубика каждая грань появляется случайным образом с определенной вероятностью. Количество играющих необходимо задать в начале партии. Цель игры – набрать как можно больше очков.

Правила игры и программа на языке БЕЙСИК приведены в журнале [22]. Основные правила игры.

Очередность: за один круг каждый игрок получает право на бросок костей, состоящий из одного, двух или трех ходов (по желанию).

Результат хода: верхние грани брошенных костей образуют комбинацию из пяти чисел, например, 2, 5, 2, 6, 1.

Цель броска: добиться выигрышной комбинации из значений костей. Очки за бросок состоят из очков за комбинацию и премий.

Очки за комбинацию: сумма значений костей, образующих комбинацию.

Премии: если комбинация выброшена с первого хода, то сумма очков комбинации умножается на 2. За комбинацию покер (все пять одинаковых) к сумме очков прибавляется 50.

Комбинации: существует 15 комбинаций, образующих две группы: обязательные (школа) и необязательные.

Необязательные:

1. Сумма- любой набор костей (стоит: сумма значений костей);

2. Двойка- две одинаковые кости есть в наборе (3 5 6 1 3);

3. Тройка- три одинаковые кости (4 1 5 4 4);

4. Две двойки- две пары одинаковых костей (1 6 5 6 1);

5. Каре- четыре одинаковые кости (3 3 3 5 3);

6. Стрит малый- фиксированная комбинация от 1 до 5 (2 3 5 1 4);

7. Стрит большой- фиксированная комбинация от 2 до 6(2 3 4 5 6);

8. Фулл- двойка и тройка (6 6 5 5 5);

9. Покер- все пять одинаковых (4 4 4 4 4).

Школа: шесть фиксированных комбинаций: три единицы; три двойки; три тройки; три четверки; три пятерки; три шестерки.

Победитель: игрок, набравший наибольшее количество очков.

Указание: написать программу игры на алгоритмическом языке высокого уровня.