4.2 Распределение расстояний между молекулами газа

Пространство заполняет газ. Вероят­ность встретить молекулу газа внутри бесконечно малого объема dv равна adv. Для любой молекулы в любой момент времени найдется какая-то молекула- ближайший сосед. Расстояние до ближайшего соседа есть случайная вели­чина. В разные моменты времени она различна. Найти плотность распределения расстояния молекулы до ближайшей частицы [1].

Для того чтобы ближайший сосед нахо­дился на расстоянии, заключенном между r и r + dr, не­обходимо, 1) чтобы расстояние до ближайшего соседа было не меньше r- вероятность этого события равна ; 2) чтобы внутри сферического слоя 4πr²dr была молекула- вероятность этого события равна a4πr²dr. Так как эти два события взаимно независимы, то вероят­ность, что произойдет и то, и другое, равна произведению их вероятностей. Следовательно, . Дифференцируя по r и имея в виду , получаем

. Деля обе части на и интегрируя, находим . Постоянная интегрирования находится из условия норми­ровки, т.е. .

Из полученного выражения следует, что при возрастании r плотность ве­роятности расстояния до ближайшего соседа растет от нуля, достигает максимума при , а затем убывает, стремясь к нулю.

4.3 Радиоактивный распад изотопа

Вероятность распада ядра не зависит от того, как долго ядро существует, не распадаясь. Какова вероятность распада изотопа в момент времени t ? Найти зависимость между постоянной распада и временем полураспада Т_1/2. Найти плотность распределения времени распада радиоактивного изотопа и среднее время распада.

Если - вероятность распада в единицу времени, то вероятность того, что ядро не распа­дается за время dt, равна 1 - . В промежутке времени t промежуток времени dt содер­жится t/dt раз. Вероятность того, что в момент времени t изотоп распадется, равна, согласно теореме умножения вероятностей, произ­ведению t/dt множителей (вероятностей того, что изотоп не распадется до данного момента времени), т.е. .

Считая dt бесконечно малым, получим после предельного перехода . Полагая , приходим к закону радиоактивного распада .

Если вероятность того, что изотоп распадется за время Т_1/2, равна 1/2, то Т_1/2 называется временем полурас­пада. Таким образом, находим .

Вероятность того, что распад произой­дет в интервале времени [t + dt], равна вероятности того, что изотоп не распадается за время t, умноженной на вероятность того, что он распадается за следующий проме­жуток времени dt. Следовательно, и , а среднее время распада изотопа .

4.4 Флуктуации и биномиальный случай

Любое физическое измерение производится с определенной точностью. Причем точность измерения, как правило, определяется конструкцией прибора и методикой измерений. Но существуют принципиальные физические ограничения точности измерений связанные с флуктуацией физических величин [28].

Например, макроскопические параметры термодинамической системы в тепловом равновесии не являются строго постоянными, а испытывают малые беспорядочные колебания вблизи некоторых средних значений. Флуктуации- это хаотические отклонения физических величин от их средних значений, вызываемые тепловым движением образующих систему частиц [2].

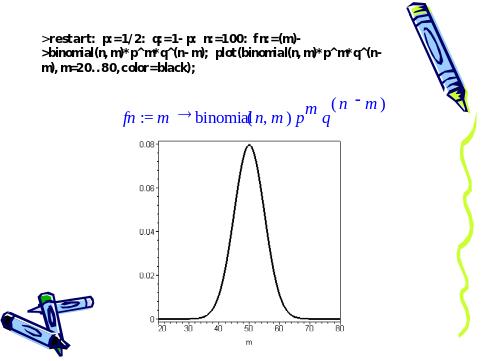
Слайд 25. Асимптотика биномиального распределения вероятностей для газа с n=100

Основные закономерности флуктуаций видны на примере пространственного распределения молекул идеального газа внутри сосуда в состоянии термодинамического равновесия.

Вероятность того, что в половине сосуда находится m частиц из полного их частиц n, можно найти в предположении, что вероятность нахождения одной молекулы в определенной половине сосуда равна ½ и не зависит от положения других частиц. В этом случае применима модель независимых случайных испытаний с биномиальным распределением вероятностей (или схемой Бернулли) , где q=1-p.

Заметим, что при больших n пользоваться формулой Бернулли затруднительно, поэтому удобнее воспользоваться асимптотикой Лапласа , где , а , т.е. огибающая распределения переходит в нормальное распределение Гаусса (слайд 24).

Вероятность того, что в n независимых испытаниях событие появится от m₁ до m₂ раз определяется интегральной теоремой Лапласа , где , а [17].

Флуктуация физической величины характеризуется стандартным отклонением распределения, т.е. корнем из дисперсии. Причем, с увеличением n флуктуация растет , а относительная флуктуация убывает .