Моделирование движения микрочастицы в свободном пространстве с помощью интегрального пакета прикладных программ MathCad

Рассмотрим движение электрона, обладающего энергией E=10 эВ и двигающегося в направлении оси x. Для моделирования электрона воспользуемся выражением (25) для волновой функции микрочастицы, связанной с вероятностью нахождения электрона в объеме пространства с координатой x в момент времени t. Запишем исходные данные:

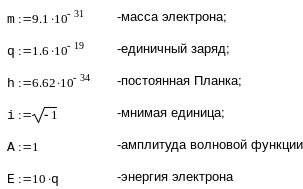
Для определения угловой частоты воспользуемся формулой Планка для энергии фотона:

Для определения волнового числа k воспользуемся выражением для энергии электрона E через импульс p и формулой де-Бройля для импульса электрона p через волновое число k:

Полагая, что произведения k·x и не превышают единицы, оценим порядки x и t:

Зададимся интервалом изменения переменной x:

.

Выберем два момента времени ,

где

.

Волновая функция для выбранных моментов времени запишется:

.

Построим графики действительной части волновой функции и

Рис.1. График изменения действительной части волновой функции свободно двигающейся частицы от пространственных координат и времени

Вероятность нахождения частицы в объеме пространства с ко-ординатой x определится как квадрат действительной части волновой функции . Построим эти графики для моментов времени t₁ и t₂:

Рис.2. Графики плотности вероятности нахождения частицы в объеме пространства с координатой x в заданный момент времени

Моделирование волнового пакета Определение волнового пакета

Монохроматическая волна, представляющая собой либо плоскую волну, либо сферическую волну, которые включают в себя одну час-тотную компоненту, является физической абстракцией. В реальных условиях с распространением любого волнообразного процесса связа-но распространение волнового пакета, состоящего из группы волн, ко-торые близки по своей длине и направлению распространения. Простейшим примером группы волн может являться импульс света, который можно сформировать с помощью затвора, открываемого на ограниченный промежуток времени . Пространственные размеры импульса света будут определяться расхождением пучка лучей после прохождения отверстия, закрываемого затвором.

В том случае, если затвор остается открытым в течение времени, при котором пространственная длина импульса света с будет много больше диаметра пучка, то можно полагать, что это одномерный слу-чай, так как изменение импульса в направлении, перпендикулярном направлению распространения, не происходит.

В общем случае импульс является трехмерным. Его пространст-венная длина определяется скоростью распространения, а диаметр размером отверстия затвора.

Другим примером волнового пакета является распространение группы частиц, каждая из которых будет формировать монохромати-ческую волну. Эти волны будут близки по своей длине и направлению распространения.