
- •Введение
- •Уравнение Шредингера для стационарного случая
- •Собственные волновые функции и собственные значения оператора Гамильтон
- •Уравнение Шредингера для свободной частицы, двигающейся в направлении оси
- •Моделирование движения микрочастицы в свободном пространстве с помощью интегрального пакета прикладных программ MathCad
- •Моделирование волнового пакета Определение волнового пакета
- •Волновая функция волнового пакета
- •Моделирование волнового пакета
- •Заключение
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа №2 движение микрочастиц в поле потенциальных сил. Движение микрочастиц через потенциальный барьер Определение потенциального барьера
- •Уравнение Шредингера для частицы двигающейся через потенциальный барьер
- •Коэффициенты отражения и прозрачности.
- •Туннельный эффект
- •Лабораторное задание
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа № 3
- •Исследование зонной структуры твердых тел
- •Строение вещества и коллективизированные электроны
- •В кристалле
- •Приближения при решении уравнения Шредингера для кристалла
- •Приближение слабосвязанных электронов.
- •Движение электрона в кристаллической решетке Модель Кронига-Пенни
- •Уравнение Шредингера для модели Кронига-Пенни
- •Решение уравнения Шредингера
- •Определение волнового числа
- •Зоны Бриллюэна. Модель приведенных зон
- •Заполнение зон электронами и классификация энергетическихзон
- •Зонная структура и электрические свойства твердых тел
- •Энергетическая структура алмазоподобных полупроводников.
- •Лабораторное задание
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа №4 исследование статистических свойств носителей заряда в полупроводниках и металлах Химический потенциал невырожденного идеального газа. Энергия Ферми.
- •Распределение Ферми-Дирака при абсолютном нуле
- •Вычисление энергии Ферми
- •Изменение энергии Ферми при изменении температуры
- •Собственные и примесные полупроводники
- •Ec ev δEg запрещенная зона валентная зона зона проводимости
- •Статистика носителей заряда в собственном полупроводнике
- •Статистика носителей заряда в примесных полупроводниках
- •Уровень Ферми носителей заряда в примесном полупроводнике n-типа
- •Статистика носителей заряда в примесном полупроводнике p-типа
- •Уровень Ферми носителей заряда в примесном полупроводнике p-типа
- •Лабораторное задание:
- •Контрольные вопросы
- •Расчет концентраций равновесных носителей заряда в приконтактной области
- •Расчет уровней Ферми электронов и дырок в приконтактной области
- •Расчет потенциального барьера контакта двух полупроводников
- •Расчет концентрации неравновесных носителей заряда контакта двух полупроводников.
- •Расчет ширины области обедненной носителями заряда.
- •Расчет барьерной емкости контакта двух полупроводников
- •Расчет диффузионной длины носителей зарядов контакта двух полупроводников
- •Расчет тока проводимости контакта двух полупроводников
- •Расчет диффузионной емкости контакта двух полупроводников
- •Лабораторное задание
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа №6 исследование электропроводности транзисторной структуры Физические процессы в транзисторной структуре
- •Расчет коэффициента передачи тока транзисторной структуры
- •Расчет концентрации неосновных носителей в области базы
- •Расчет плотности тока неосновных носителей в области базы
- •Расчет токов эмиттерного и коллекторного переходов
- •Эквивалентная схема биполярного транзистора
- •Эквивалентная схема биполярного транзистора в виде четырехполюсника
- •Эквивалентная схема биполярного транзистора
- •Расчет параметров элементов эквивалентной схемы транзисторной структуры
- •Математическая модель биполярного транзистора и расчет переходов
- •Расчет электрических параметров схемы с биполярным транзистором с использованием эквивалентной схемы
- •Лабораторное задание
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа №7 физические процессы в полевых транзисторах Конструктивные особенности полевых транзисторов с изолированным затвором
- •Физические процессы в транзисторе
- •Эффективная подвижность носителей заряда в канале
- •Концентрация подвижных носителей в области канала
- •Напряжение отсечки
- •Ширина канала полевого транзистора
- •Вольтамперная характеристика полевого транзистора
- •Входная и выходная характеристики полевого транзистора
- •Лабораторное задание
- •Содержание
Расчет коэффициента передачи тока транзисторной структуры
Коэффициент передачи тока транзисторной структуры опреде-ляется отношением полного тока коллектора ik к полному току эмит-тера iэ:
![]() .
(1)
.
(1)
С другой стороны, полные токи коллектора и эмиттера могут быть определены через такие параметры, как эффективность эмитте-ра, коэффициент переноса и коэффициент умножения в коллекторе.
Эффективность
эмиттера
![]() определяется как отношение элек-тронного
тока эмиттера inэ
к полному току эмиттера:
определяется как отношение элек-тронного
тока эмиттера inэ
к полному току эмиттера:
![]() .
(2)
.
(2)
Коэффициент
переноса
![]() характеризует количество электронов,
оставшихся после рекомбинации в базе,
и определяется отношением электронного
тока коллектора inк
к электронному току эмиттера:
характеризует количество электронов,
оставшихся после рекомбинации в базе,
и определяется отношением электронного
тока коллектора inк
к электронному току эмиттера:
![]() .
(3)
.
(3)
Коэффициент
умножения в коллекторе
![]() показывает, во сколько раз полный ток
коллектора iк
больше электронного тока коллектора:
показывает, во сколько раз полный ток
коллектора iк
больше электронного тока коллектора:
![]() .
(4)
.
(4)
Рассматривая совместно все эти выражения, получим для коэффициента передачи тока:
![]() .
(5)
.
(5)
Расчет концентрации неосновных носителей в области базы
Для расчета концентрации электронов в области базы воспользу-емся уравнением непрерывности, полагая, что кроме тепловой генера-ции носителей заряда в области базы, другие виды генерации отсутст- вуют.
 ,
(6)
,
(6)
где npo – равновесная концентрация электронов в области базы;
Ln – диффузионная длина электронов.
Решение уравнения непрерывности может быть записано в виде:
![]() ,
(7)
,
(7)
где A и B – постоянные интегрирования.
Для определения постоянных A и B запишем решение уравнения непрерывности в виде гиперболических функций:
![]() ,
(8)
,
(8)
где C и D – постоянные.
Выберем начало
координат оси x
между эмиттером и коллекто-ром в
области базы. Если ширину базы
обозначить
![]() ,
то границы эмиттера и коллектора будут
иметь координаты
,
то границы эмиттера и коллектора будут
иметь координаты
![]() и
и
![]() соответст-венно. В этом случае решение
уравнения непрерывности эквивалент-но
следующему выражению:
соответст-венно. В этом случае решение
уравнения непрерывности эквивалент-но
следующему выражению:
 ,
(9)
,
(9)
где G и F могут быть найдены из граничных условий.
Граничными условиями, могут быть значения концентрации элек-тронов в эмиттерной и коллекторной областях, которые определяют-ся:
![]() ,
(10)
,
(10)
![]() ,
(11)
,
(11)
где uЭБ и uКБ – постоянные напряжения на эмиттерном и коллекторном переходах.
Подставляя в решение уравнения непрерывности вместо текущей координаты значение координат эмиттерного и коллекторного перехо-дов, получим:
![]() ,
(12)
,
(12)
![]() .
(13)
.
(13)
Из этих выражений постоянные F и G определяются:
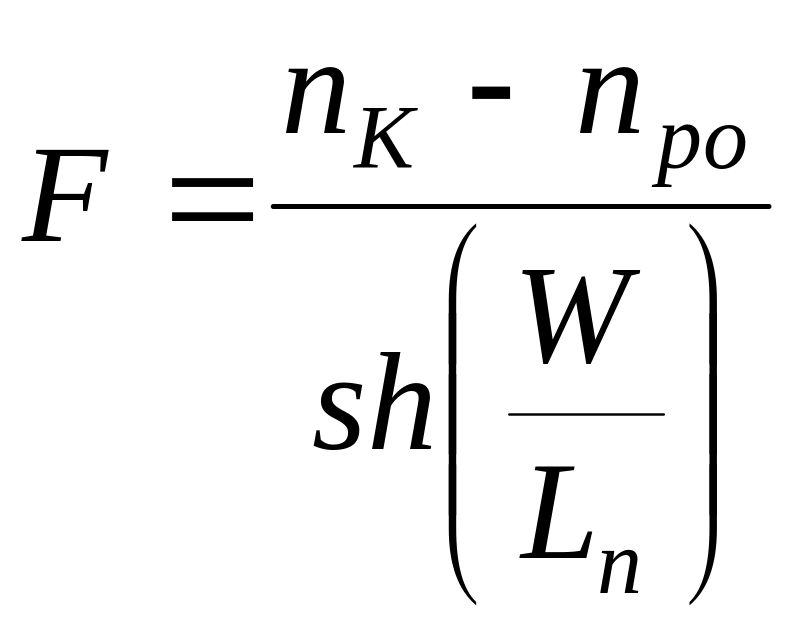 ,
(14)
,
(14)
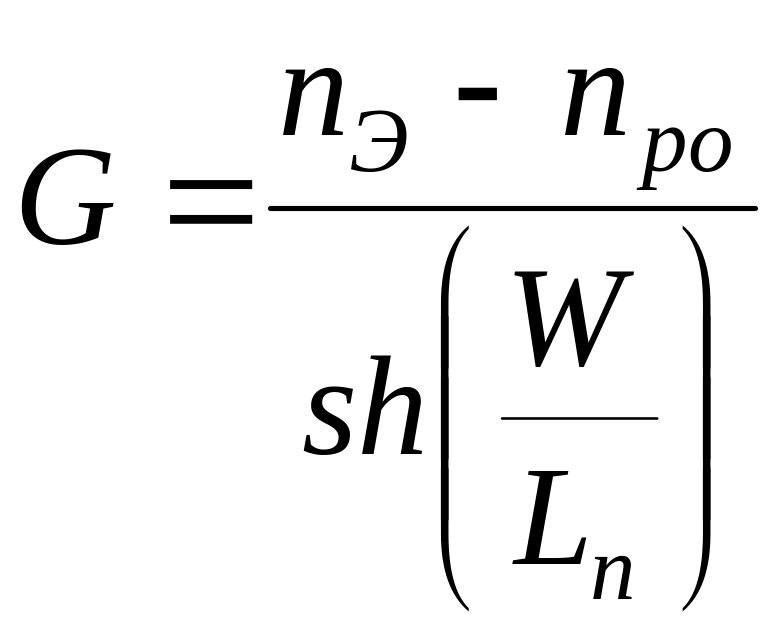 .
(15)
.
(15)
