7. Функция распределения

Очевидно, число частиц в единице объема, скорости которых лежат в некотором интервале от до тем больше, чем больше интервал , т.е.

, (3.39)

где - коэффициент пропорциональности. Надо отметить, что зависит и от самой скорости. При одинаковых по величине интервалах , но при разных абсолютных значениях скорости число частиц будет различным. Это означает, что коэффициент пропорциональности в формуле (3.39) должен быть функцией скорости:

.

Кроме того, должно быть также пропорционально числу частиц в единице объема и, таким образом, окончательно получаем:

. (3.40)

Эту формулу также записывают в виде

, (3.41)

где - доля частиц, скорости которых лежат в интервале от до .

Функцию называют функцией распределения. Если , то .

8. Таким образом, функция распределения численно равно доле частиц, скорости которых лежат в единичном интервале скоростей вблизи . Существуют несколько методов определения функции распределения . Функция распределения молекул по компонентам скорости можно получить из барометрической формулы (см. учебники Кикоин И.К., Кикоин А.К. "Молекулярная физика"). Она имеет вид:

, (3.42)

где - так называемая нормировочная постоянная. Знание функции позволяет определить, какая часть молекул в единице объема обладает скоростями от до , т.е.

. (3.43)

Эта величина не зависит от того, каковы составляющие скоростей молекул по осям Х и У. Поскольку в пространстве нет выделенных направлений, соотношение вида (3.43) справедливо для осей Х и У, т.е.

, (3.44)

.

Найдем значение , входящее в выражения (3.43) и (3.44). Для этого перепишем одно из них, например, (3.43) в виде:

.

- это число молекул в единице объема, составляющие скорости которых по оси лежат в пределах от до . Если просуммировать это выражение по всем возможным значениям от -¥ до +¥, то получим общее число молекул в единице объема, т.е. , поскольку каждая молекула обладает какой-либо составляющей скорости по оси . Таким образом,

,

откуда

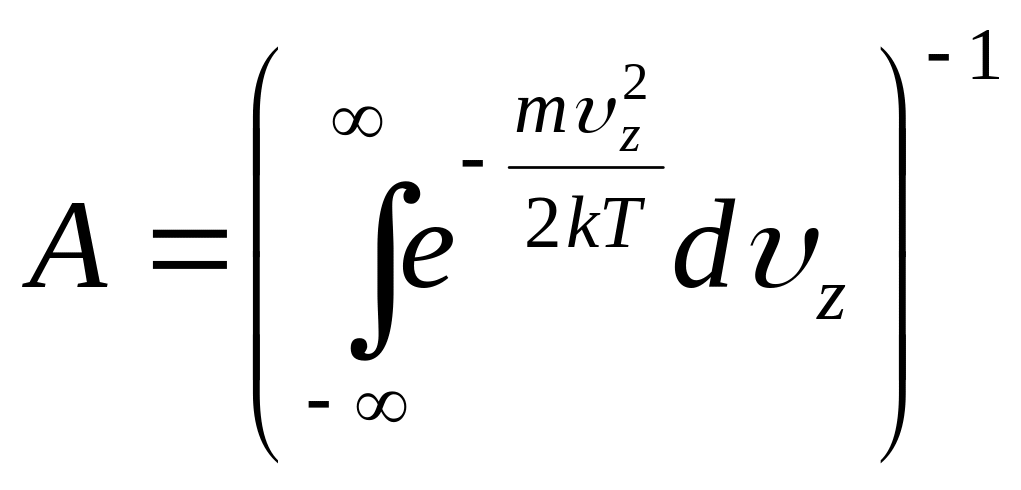. (3.45)

Для вычисления интеграла (3.45) введем новую переменную .

Тогда

и .

Отсюда

.

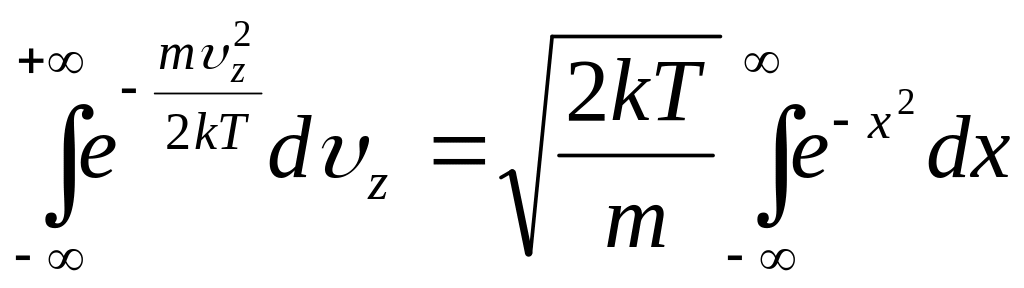Известно, что . Тогда из (3.45) имеем:

. (3.46)

Следовательно, выражение для примет теперь вид:

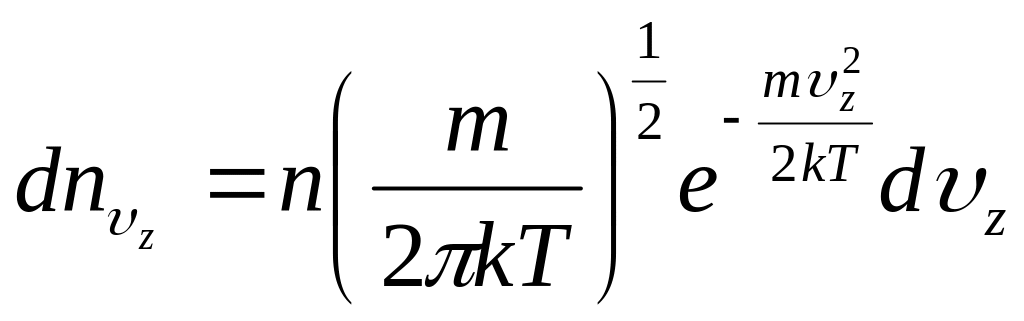. (3.47)

Определим число молекул в единице объема, обладающих скоростями, составляющие которых по трем осям координат лежат в пределах от до (по оси Х), от до (по оси У) и от до (по оси Z). Будем рассуждать следующим образом. Отберем сначала из всех молекул в единице объема те молекулы, составляющие скоростей которых по оси Х лежат в пределах от до . Число таких молекул согласно (3.44), равно

.

По осям У и Z составляющие скоростей этих молекул могут быть любыми (от

- до + ). Какая часть из этого числа имеет скорости, составляющие которых по оси У лежат в пределах от до при любых . Согласно (3.44) для определения этого числа надо умножить на . Значит, число молекул, у которых составляющие скорости по оси Х лежат в пределах от до и в то же время по оси У в пределах от до равно:

.

Рассуждая таким же образом можно получить выражение для числа молекул , компоненты скорости которых одновременно лежат в пределах , ,

.

Подставляя в полученную формулу выражение (3.46) для , получим окончательно:

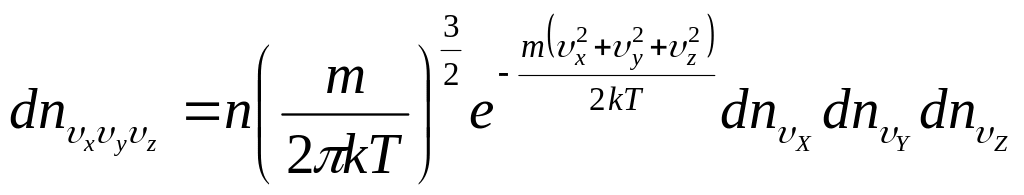. (3.48)

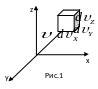
Дадим геометрическое истолкование этой формулы. Представим, что все молекулы, компоненты скоростей которых заключены в указанном выше интервале скоростей, собраны в начале координат и выпущены. Через одну секунду они все окажутся на расстоянии от начального положения в кубике со сторонами ,т.е. в объеме . Концентрация молекул в этом кубике равна:

, (3.49)

где .

_ _____________________________________________