9. Формула Максвелла

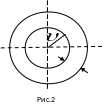Концентрация, определяемая формулой (3.49) не может зависеть от направления вектора скорости . Поэтому мы можем найти функцию распределения молекул по скоростям, независимо от их направления. Действительно, если собрать все молекулы единицы объема, скорости которых лежат в пределах от до , независимо от их направления и выпустить их, то они, разлетаясь по всем направлениям, через одну секунду окажутся равномерно распределенными в шаровом слое толщиной и радиусом . Это шаровой слой сложится из тех «кубиков», о которых говорилось выше. Плотность числа молекул или концентрация будет определяться опять формулой (3.49).Число молекул в шаровом слое будет равно произведению плотности молекул (формула (3.49) на объем шарового слоя , т.е

(3.50)

Если сравнить эту формулу с выражением (3.40), получим следующее выражение для функции распределения молекул по скоростям:

. (3.51)

Эта функция называется функцией распределения Максвелла.

В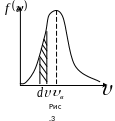 ид этой функции приведен на рис. 3. Как видно из графика, функция обращается в нуль при и , т.е. число неподвижных молекул, как и число молекул, движущихся с очень большой скоростью, равна нулю. Из кривой видно, что существует такая скорость , которой обладает максимальная доля молекул. Эта скорость называется наивероятнейшей скоростью.

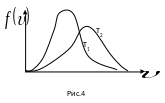
Пользуясь кривой распределения Максвелла, можно графически определить число молекул, обладающих скоростями в заданном интервале и . Это число выражается площадью с основанием и высотой . Распределение молекул по скоростям по формуле (3.51) зависит от температуры газа. Эта зависимость приведена на рис.4, из которого следует, что с повышением температуры скорости молекул возрастают, и вся кривая смещается в сторону больших скоростей. Площади, ограниченные этими кривыми и осью скоростей, пропорциональны общему числу частиц и не могут изменяться с температурой. Вследствие этого, максимумы кривых с повышением температуры понижаются. Надо отметить, что распределение Максвелла по скоростям является равновесным распределением. При отклонении система от состояния равновесия, максвелловское распределение нарушается. При возвращении в состояние равновесия благодаря столкновениям устанавливается опять максвелловское распределение.

Распределение Максвелла связано хаотичным движением молекул. Движение молекул полностью хаотично, если они распределены по скоростям в соответствии с формулой Максвелла. В противном случае, движением молекул является частично упорядоченным.

10. Средняя арифметическая, средняя квадратичная и наивероятнейшая скорости молекул

Используя функцию распределения Максвелла можно вычислить значение средней скорости молекул. Согласно определению, средняя скорость определяется выражением

,

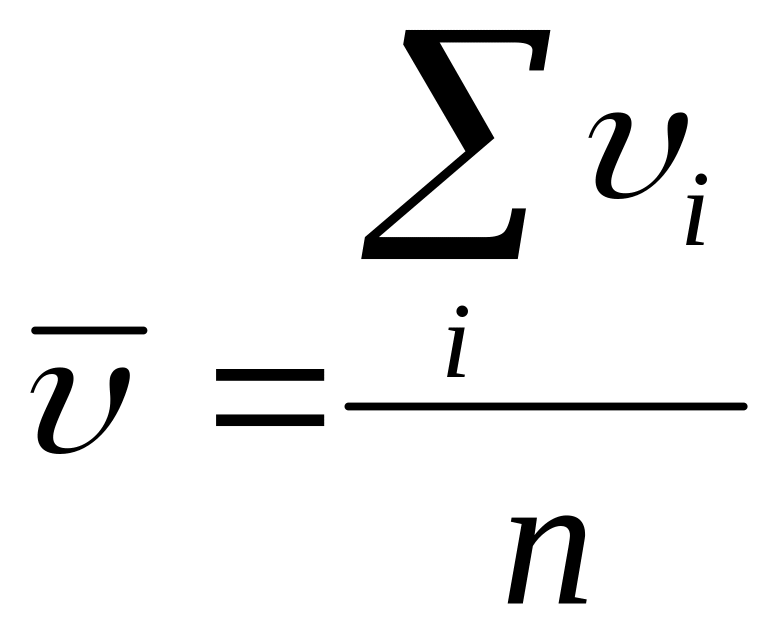где - скорость той молекулы. Сумму скоростей молекул можно найти из следующих соображений: - это число молекул единицы объема, скорости которых заключены в интервале от до вблизи значения . Умножив это выражение на , получим сумму скоростей этих молекул, равную . Тогда представляет сумму скоростей всех молекул в единице объема. Следовательно, средняя арифметическая скорость равна:

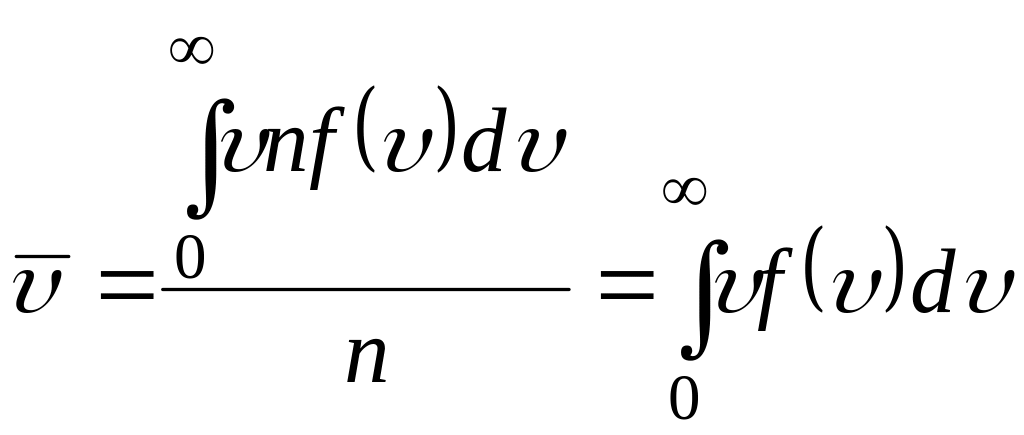. (3.52)

Используя выражение (3.51) для функции распределения Максвелла , можем записать:

.

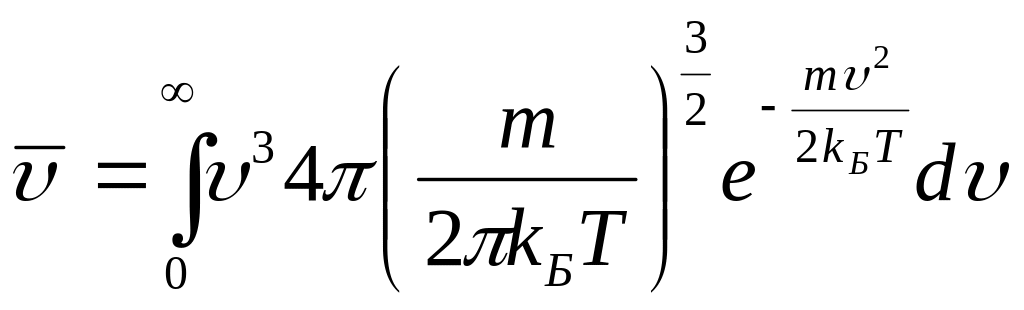Интегрируя по частям, имеем:

.

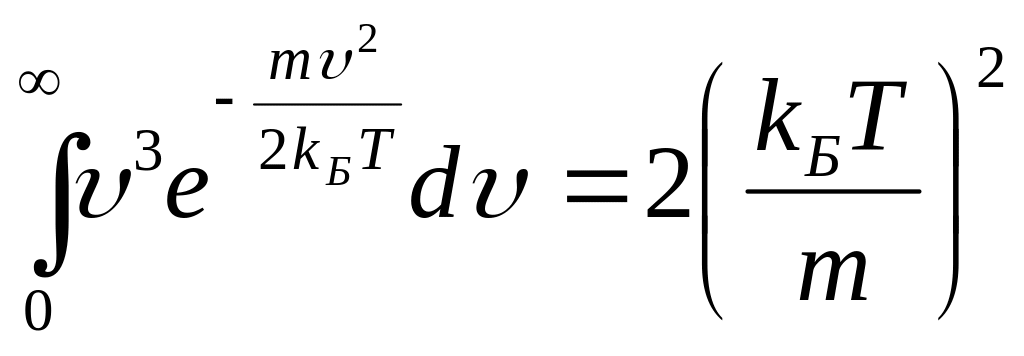Подставляя это значение интеграла в формулу (3.52), получим:

. (3.53)

Для определения среднеквадратичной скорости, воспользуясь формулой (3.52), определим среднее значение квадрата скорости :

.

Поставив в эту формулу выражение для функции распределения Максвелла, получим:

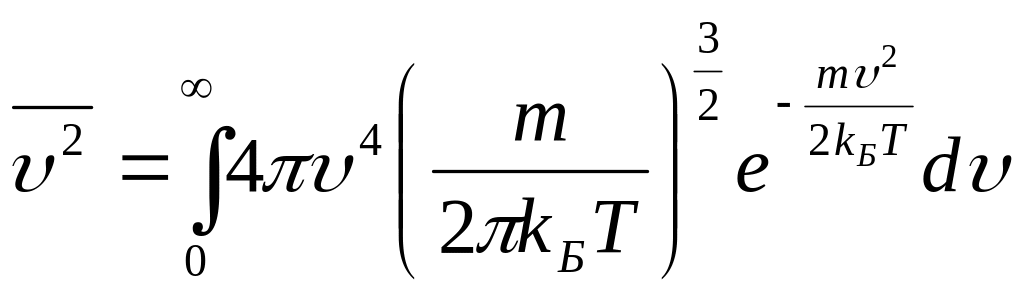. (3.54)

Интегрируя по частям, можно показать, что

,

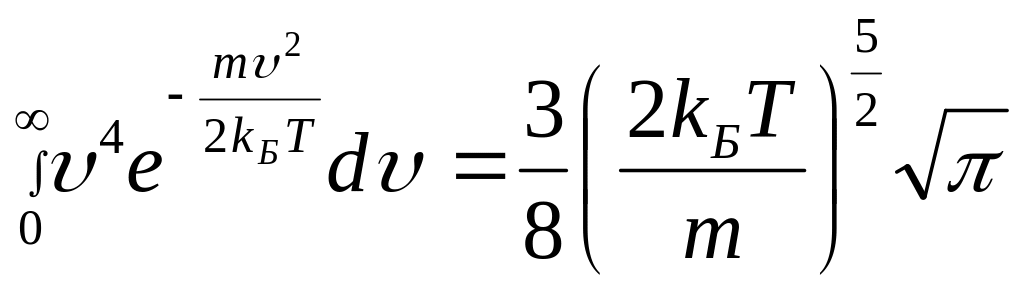откуда

.

Тогда среднеквадратичная скорость будет равна:

= . (3.55)

Вычислим теперь наивероятнейшую скорость молекул , которую имеют наибольшее число молекул газа. При этой скорости кривая распределения Максвелла проходит через максимум. Для определения напишем условие максимума функции распределения Максвелла:

.

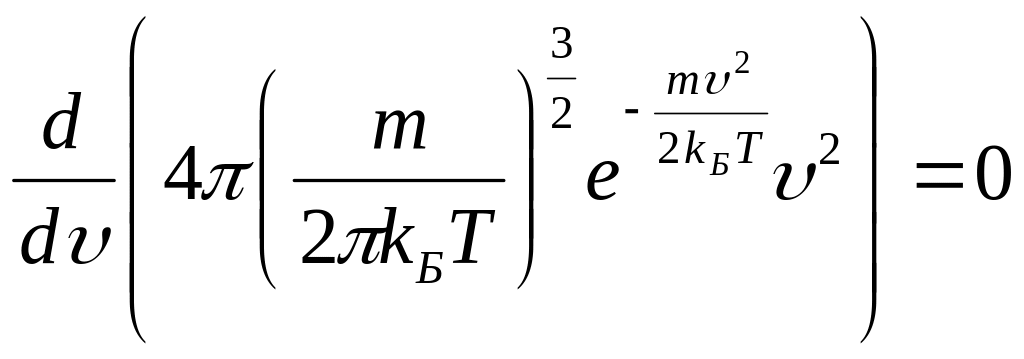Дифференцируя это выражение, получим:

,

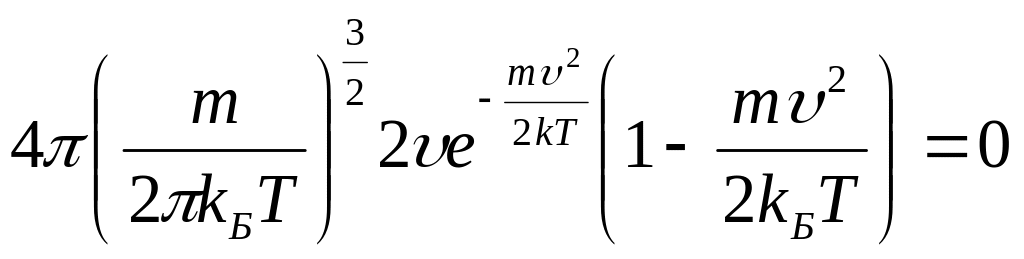Это равенство может быть выполнено либо при , либо при , или при условии . Очевидно, что первые два случая не соответствуют максимуму кривой. Следовательно, наивероятнейшая скорость определяется из условия , откуда

. (3.56)

Сравнивая выражения (3.53), (3.55) и (3.56), найдем соотношения между тремя вычисленными скоростями:

.