52. Условия равновесия на границе двух сред. Краевой угол

Рассмотрим условия, возникающие на границе соприкосновения двух несмешивающихся друг с другом жидкостей.

Пусть капля жидкости 2 помещена на поверхности другой жидкости 1 (рис.2). В зависимости от видов жидкостей капля второй жидкости может иметь вид чечевицы или же образовать пленку. Рассмотрим, при каких условиях образуется чечевица, а при каких - тонкая пленка. В рассматриваемом случае граничат друг с другом следующие среды: жидкость 1 граничит с жидкостью 2, жидкости 1 и 2 граничат со средой 3. Среда 3 – это смесь паров жидкостей 1 и 2 с воздухом. Границей соприкосновения трех сред является окружность, ограничивающая чечевицу. На элемент длины этой окружности действуют три силы поверхностного натяжения:

- сила на границе между жидкостями 1 и 2;

- сила на границе жидкость 1-газ;

- сила на границе жидкость 2-газ.

Каждая из этих сил направлена по касательной к поверхности соприкосновения соответствующих сред. Чтобы жидкость 2 находилась в равновесии, необходимо, чтобы сумма проекций всех трех сил на оси координат равнялись нулю, т.е.

, , (6.4)

или

, . (6.5)

Возведя оба эти равенства в квадрат, и сложив их, получим:

),

или

. (6.6)

У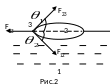 равнениями (6.5) и (6.6) определяются углы и . Углы называются краевыми углами. Краевые углы определяются соотношением трех коэффициентов . В частности, соотношение между коэффициентами может быть таким, что , т.е. . Тогда жидкость 2 растекается тонким слоем по поверхности жидкости 1. В этом случае говорят, жидкость 1 полностью смачивается жидкостью 2. Физически это означает, что сила по величине больше равнодействующей сил , или . Если , то жидкость будет стягиваться до тех пор, пока не станет равной . Это и есть условие образования чечевицы.

53. Силы, возникающие на кривой поверхности жидкости

Кривизна поверхности жидкости приводит к появлению сил, действующих на жидкость под этой поверхностью.

Р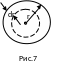 ассмотрим сферическую каплю радиусом (рис.7).

При увеличении радиуса сферы растет площадь его поверхности, а вместе с ней и поверхностная энергия. А это может происходить только за счет совершения работы внешними силами. Наоборот, при уменьшении радиуса капли поверхностная энергия уменьшается. Это значит, что работа производится силами, действующими в самой капле. Если на каплю не действуют внешние силы, то они стремятся занять наименьший объем, т.е. объем жидкости под сферической поверхностью всегда несколько сжат. Это приводит к тому, что жидкость в капле испытывает дополнительное давление, направленное радиально перпендикулярно к ее поверхности. Пусть под действием этого давления жидкий шар уменьшит объем на . При этом производится работа сжатия жидкости за счет уменьшения поверхностной энергии капли. Работа сжатия равна:

, (6.7)

а уменьшение поверхностной энергии равна:

, (6.8)

где - уменьшение поверхности шара, связанное с уменьшением радиуса капли на . Для шара и . Отсюда следует:

.

Подставляя эти значения для и в (6.7) и (6.8) и принимая во внимание, что , получаем:

,

откуда имеем для давления, оказываемого на жидкость ее кривой поверхностью следующее выражение:

. (6.9)

Если поверхность жидкости цилиндрическая, то

,

где - длина цилиндра. Соответственно

.

Подставляя эти значения и в формулы (6.7) и (6.8) аналогично получим:

. (6.10)

В общем случае поверхности любой формы давление, обусловленное кривизной поверхности, выражаются уравнением, известным под названием уравнения Лапласа:

, (6.11)

где и - главные радиусы кривизны для данного элемента поверхности.

В случае сферы = и формула (6.11) переходит в (6.9). В случае цилиндра один из главных радиусов равняется , а другой совпадает с радиусом цилиндра. Соответственно, формула (6.11) переходит в (6.10). Дополнительное давление, определяемое формулой (6.11) направлено к центру кривизны поверхности.