24. Диффузия

П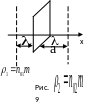 усть в некотором объеме газа имеет место неоднородность в отношении плотности , причем плотность убывает в направлении оси Х. Предположим,

что плотности на расстоянии влево и вправо от площади , равны соответственно и (Рис.9). Тогда > . Поскольку , где - масса молекулы, одинаковое для всех молекул газа, . Переносимой величиной в случае диффузии является масса, т.е. . Тогда в выражении (4.3)

, .

Окончательно имеем:

. (4.4)

- масса газа, переносимая благодаря диффузии через площадь , перпендикулярной направлению оси Х, за время . В термодинамике необратимых процессов уравнение диффузии определяется эмпирическим законом Фика:

, (4.5)

где D- коэффициент диффузии. Из уравнений (4.4) и (4.5) следует, что коэффициент диффузии определяется следующим выражением:

. (4.6)

Единица измерения коэффициента диффузии в системе СИ .

Рассмотрим, как зависит коэффициент диффузии от термодинамических параметров. Из формулы (4.6) следует, что , поскольку не зависит от давления, а . Таким образом, с ростом давления Р коэффициент диффузии уменьшается. Определим зависимость коэффициента диффузии от температуры. Так как длина свободного пробега практически не зависит от температуры, а , имеем . Кроме того, D зависит от сорта газа, эта зависимость определяется тем, что в выражении для коэффициента диффузии входит молярная масса газа .

25. Теплопроводность газов

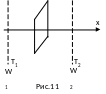
Пусть в некотором объеме газа температура Т убывает в направлении оси Х, т.е. (рис.11). Поскольку кинетическая энергия молекулы определяется как , . Поэтому в сторону убывания температуры будет происходить преимущественный перенос энергии, следовательно, и теплоты. В случае данной задачи переносимый молекулами физической характеристикой является

кинетическая энергия, т.е. . Будем считать, что одинакова во всем объеме. Тогда величины, входящие в уравнение переноса, выразятся следующим образом:

,

где ,

.

- количество внутренней энергии, переносимое за время через площадку перпендикулярно направлению переноса. Подставляя эти выражения в уравнение переноса (4.3), получим:

. (4.11)

Умножив числитель и знаменатель уравнения (4.11) на , где -масса молекулы, -число Авогадро и учитывая, что , перепишем (4.11) в виде:

, (4.12)

где -молярная теплоемкость при постоянном объеме, -молярная масса. Так как -удельная теплоемкость, из (4.11) окончательно получим уравнение теплопроводности:

. (4.13)

Эмпирически явление теплопроводности описывалось уравнением Фурье

, (4.14)

где называется коэффициентом теплопроводности. Из (4.13) и (4.14) следует, что выражение для коэффициента теплопроводности имеет вид:

. (4.15)

Рассмотрим зависимость коэффициента теплопроводности от давления и температуры. Из входящих в (4.15) величин, только плотность и длина свободного пробега зависят от давления, причем и  . Это приводит к заключению, что коэффициент теплопроводности не зависит от давления. Этот вывод находится в превосходном согласии с опытными данными, которые показывают, что при изменении давления в широких пределах коэффициент теплопроводности остается постоянной.

Из величин, входящих в коэффициент теплопроводности (4.15), только одна величина зависит от температуры, причем , соответственно .

Как показывает опыт, коэффициент теплопроводности растет с температурой несколько быстрее, чем . Это связано с тем, что коэффициент теплопроводности зависит от длины свободного пробега. Как показали раньше, не является постоянной величиной, а растет с температурой.