§3. Рассеяние молекулярного пучка в газе

Со столкновением молекул в газе связано ослабление молекулярного пучка при прохождении через газ.

Пусть некоторое число молекул, обладающих определенной скоростью, величина и направление которой одинакова для всех молекул, проходит через газ. Из-за столкновений с молекулами, часть молекул пучка изменит направление своего движения, и будет выбывать из пучка. По мере продвижения через газ число таких молекул, покинувших пучок, будет возрастать, а число частиц в пучке будет постепенно уменьшаться.

Пусть пучок движется в газе вдоль оси Х и в начале его пути при Х=0 число частиц в пучке равно . После прохождения отрезка пути , число частиц в пучке уменьшится на некоторую величину и станет равным . Отношение числа, выбывших из пучка частиц к числу, оставшихся равно отношению пройденного пучком пути к длине свободного пробега , так как чем больше это отношение, т.е. чем больше длин свободного пробега умещаются в длине , тем больше шансов у каждой молекулы быть отклоненной при столкновении. Поэтому . Знак минус указывает, что частиц в пучке уменьшается. Интегрируя обе части этого выражения, получим:

,

где - постоянная интегрирования. Ее можно определить из условия, что при х=0 . Поэтому .

Отсюда , или , тогда .

Эта формула показывает, что с ростом толщины слоя число частиц в молекулярном пучке уменьшается по экспоненциальному закону.

23. Явление переноса в газах. Уравнение переноса

Хаотичное движение газовых молекул ведет к непрерывному перемешиванию газа. С этим связано ряд важных явлений, происходящих в газах. Например, если в разных частях сосуда с газом плотность газа различная, то с течением времени она выравнивается. Точно также два различных газа, находящихся в соприкосновении перемешиваются между собой. Эти явление называются диффузией.

В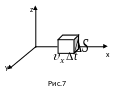 объеме газа, части которого имели первоначально различные температуры, происходит постепенное выравнивание температуры, за счет переноса молекулами своей энергии и обмена энергиями с другими молекулами при перемешивании. Это явление называется теплопроводностью. Рассмотрим еще одно явление. Пусть газ течет вдоль горизонтальной поверхности АВ. Ближайший к поверхности слой имеет меньшую скорость благодаря трению о поверхность. Скорости разных слоев газа показаны на рисунке 6. Между слоями газа возникает сила трения, обусловленная переносом молекулами из слоя в слой количества движения . Это явление называется внутренним трением или вязкостью. Благодаря внутреннему трению газ движется вблизи поверхности параллельными слоями, скорости которых убывают в направлении перпендикулярном к поверхности АВ. Все перечисленные явления обусловлены одной причиной - переносом молекулами газа своих физических характеристик: массы (диффузия), энергии (теплопроводность), количество движения (явление внутреннего трения). Поэтому механизм всех этих явлений является одинаковым, и все они объединены под общим названием - явление переноса.

Исходя из молекулярно-кинетической теории, выведем общее для всех явлений переноса уравнение переноса. В пространство, где находится газ с концентрацией , введем декартовую систему координат (рис.7).

Перпендикулярно оси Х поместим поверхность площадью . Определим количество молекул, проходящих через эту поверхность за время .

Рис.7

За время через пройдут часть всех молекул, находящихся внутри параллелепипеда с основанием и высотой . Число таких молекул будет равно

.

Эти молекулы переносят через площадку значения своих характеристик (масса, энергия, количество движения). Тогда количество физических характеристик, перенесенных молекулами в одном направлении через за время определится выражением:

.

Такое же количество физической характеристики будет перенесено и в обратном направлении, т.е. поток физической характеристики через будет равным нулю.

П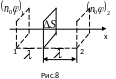 редположим, что рассматриваемый газ неоднороден по своим свойствам, т.е. различно в разных местах объема, а сами молекулы имеют неодинаковые значения . Тогда будет также различным в разных местах объема газа. Пусть убывает в положительном направлении оси Х.

Выберем две площади, находящиеся на одинаковых расстояниях от площади , равных длине свободного пробега (Рис.8). Тогда будет связано переносом физической характеристики по направлению оси Х.

Такой же поток физической характеристики в направлении оси Х будет и через площадь , так как эти площади находятся на расстоянии длины свободного пробега, и в этом промежутке обмен значениями и изменение не происходит, поскольку молекулы не испытывают столкновения. Также рассуждая, можно предположить, что через площадь в обратном направлении оси Х, будет поток физической характеристики , причем > . Тогда результирующий поток физической характеристики через будет равным:

.

Разделив и умножив правую часть полученного выражения на , перепишем в виде:

.

Поскольку представляет изменение на единицу длины, мы можем переписать выражение для в виде:

. (4.3)

Полученное выражение представляет уравнение переноса. Знак (-) обусловлен тем, что перенос физической величины происходит в направлении противоположном , определяет направление максимального роста .