4.4. Теорема Коши.

Теорема.

Пусть функции и непрерывны на и дифференцируемы на и пусть . Тогда существует точка такая, что .

Доказательство.

Введем вспомогательную функцию , которая удовлетворяет условиям теоремы Ролля: непрерывна на ; дифференцируема на , причем ; и . Тогда по теореме роля найдется точка , в которой , то есть .

Замечание. Теорема Лагранжа является частным случаем теоремы Коши, так как в теореме Лагранжа в качестве берется функция х.

4.5. Правило Лопиталя.

Теорема. Пусть функции и определены и дифференцируемы в некоторой окрестности точки и , . Тогда, если существует , то существует , причем .

Доказательство. На отрезке для и выполняются условия

теоремы Коши, тогда , где . Это равенство при учете условия принимает вид .

При также , поэтому .

Замечание.

Правило Лопиталя можно применять неоднократно.

Теорема остается в силе, если .

Правило Лопиталя можно применять, если , то есть оно позволяет раскрыть неопределенности , .

Если встречаются неопределенности , , то их надо свести к неопределенностям вида , путем тождественных преобразований. Например: .

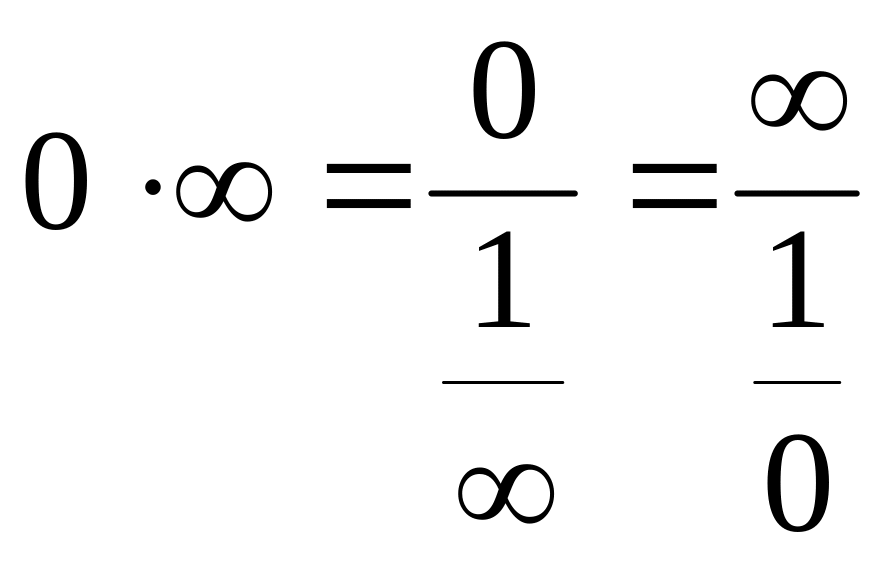Если отыскиваются пределы показательно-степенных выражений, имеющие неопределенности вида , то поступают следующим образом .

В показателе новой функции произведение даст неопределенность вида .

4.6. Формула Тейлора.

Теорема.

Пусть функция имеет в некоторой окрестности точки непрерывную производную до порядка включительно, тогда функцию можно представить в виде: , где при , - остаточный член в форме Лагранжа, .

Если в формуле Тейлора считать , то получим формулу Маклорена , где , .

Формула Тейлора позволяет представить в окрестности точки функцию в виде суммы многочлена n-й степени и остаточного члена . Она позволяет оценить ошибки в приближенных равенствах, получить приближенные равенства нового типа, вычислить приближённое значение функции с помощью арифметических операций.

Лекция 5. Применение производных к исследованию функций.

5.1.Условие монотонности функции. Определение максимума и минимума функции в точке.

5.2. Необходимое условие существования экстремума функции одной переменной.

5.3. Достаточное условие существования экстремума функции одной переменной.

5.4. Наибольшее и наименьшее значение функции на отрезке.

5.5. Определение выпуклости и вогнутости графика функции. Достаточное условие выпуклости и вогнутости графика. Необходимое и достаточное условие существования перегиба.

5.6. Асимптоты графика функции.

5.1. Условие монотонности функции. Определение максимума и минимума функции в точке.

Пусть функция определена и дифференцируема на .

Теорема 1. Если для , тогда постоянна на .

Теорема 2. Если , тогда возрастает на .

Теорема 3. Если , тогда убывает на .

Доказательство теоремы 3.

Пусть и , . Применим теорему Лагранжа к функции на : , где . Так как по условию , то и при - убывает.

Замечание. Положительность (отрицательность) производной на интервале не является необходимым условием возрастания (убывания) функции на . Так, функция возрастает на , но производная этой функции не является всюду положительной на этом интервале (в точке обращается в ноль).

Пусть функция определена на множестве X, и . Определение. Точка называется точкой локального max функции , если существует окрестность точки , для всех точек которой при .

О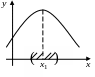 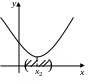пределение. Точка называется точкой локального min , если существует окрестность точки , для всех точек которой при .

Точки локального max и min функции называются экстремумами, а значение функции в этих точках - экстремальным.