Лекция 10. Интегрирование некоторых классов функций.
10.1. Интегрирование простейших рациональных дробей.
10.2. Интегрирование рациональных дробей методом разложения на простейшие дроби.
10.3. Интегрирование некоторых тригонометрических функций.
10.4. Интегрирование некоторых иррациональных выражений. Некоторые тригонометрические подстановки.
10.1. Интегрирование простейших рациональных дробей.
Отношение двух
алгебраических многочленов, называется
рациональной дробью. Простейшими
рациональными дробями называются дроби
четырех типов: 1)
;
2)
;
3)
;
4)
,
где
.
Коэффициенты
.
Простейшие дроби интегрируются в конечном виде следующим образом:
1)
;
2)
;
=
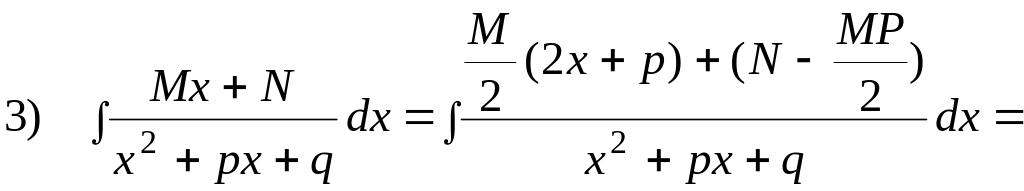
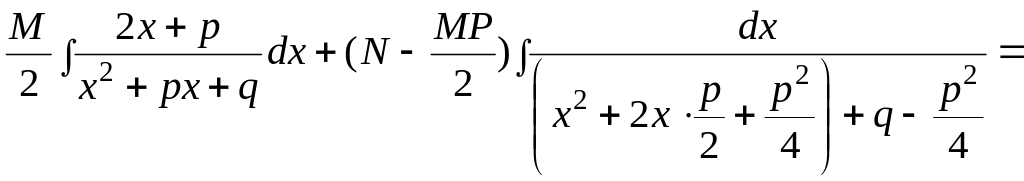
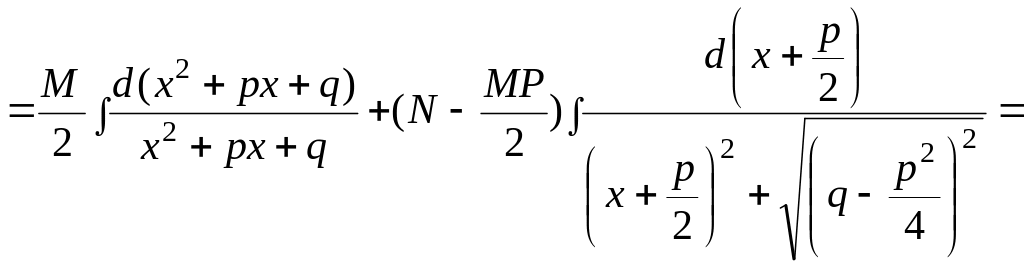
4) Дроби четвертого типа интегрируются с помощью реккурентных соотношений.
10.2. Интегрирование рациональных дробей методом разложения на простейшие дроби.
Определение. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.
Определение. Рациональная дробь называется неправильной, если степень числителя больше либо равно степени знаменателя.
Всякую неправильную дробь можно представить в виде суммы целой части и правильной дроби путем деления числителя на знаменатель. Интегрирование целой части не представляет труда. Рассмотрим случай интегрирования дробной части в зависимости от вида знаменателя.
Пусть рациональная
дробь имеет вид
.
Тогда возможны случаи. 1. Все корни
многочлена
действительные и простые, тогда
– корни
.
В этом случае правильная рациональная
дробь представляется в виде суммы дробей
первого типа следующим образом:
.
Пример.
.
2. Корни
– действительные, причем некоторые из
них кратные, тогда
,
и правильная рациональная дробь
представляется в виде суммы дробей
первого и второго типа:
.
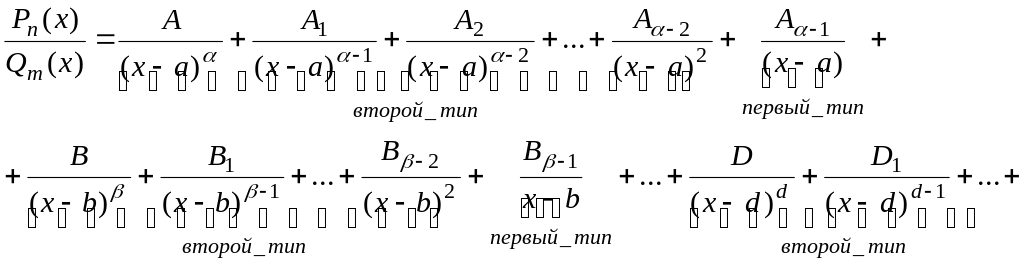
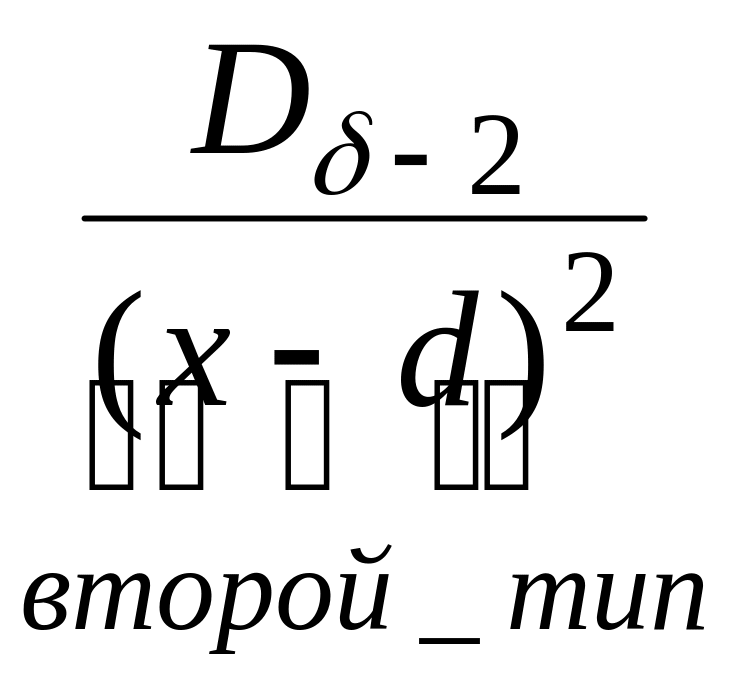
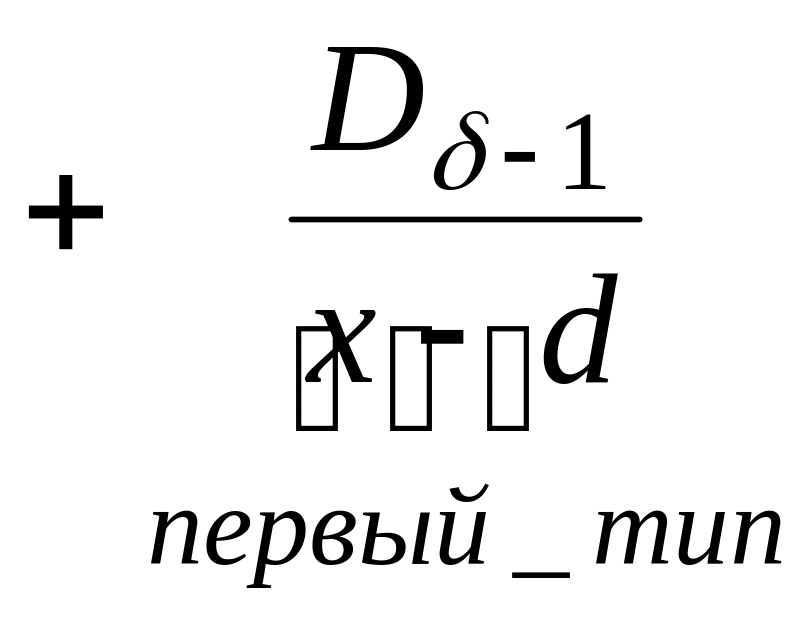Пример.
.
3. Среди корней
есть комплексно-сопряженные корни, то
есть
,
тогда каждому квадратному трехчлену с
соответствует дробь третьего типа:
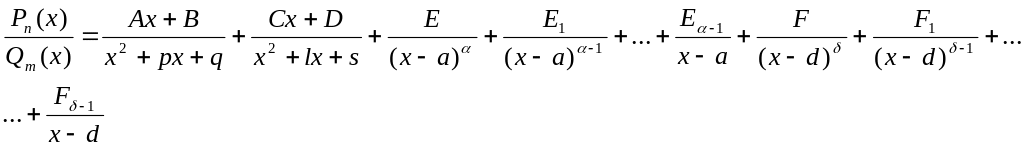
4. Среди корней
знаменателя есть комплексно-сопряженные
кратные корни, то есть
.
В этом случае рациональная дробь
представима в виде суммы дробей первого,
второго, третьего и четвертого типов.
Замечание.
Коэффициенты разложения
правильных рациональных
дробей на сумму простейших дробей находят методом неопределенных коэффициентов, который заключается в том, что сумма правых частей разложения с неизвестными коэффициентами приводится к общему знаменателю, а затем приравниваются числители левой и правой частей. Составляются уравнение или система уравнений, в которых приравниваются коэффициенты при соответствующих степенях x слева и справа.
10.3. Интегрирование некоторых тригонометрических функций.
Рассмотрим некоторые случаи интегрирования тригонометрических функций.
Универсальная
тригонометрическая подстановка для
используется, если sinx
и cosx
присутствуют в целых положительных
степенях. Подстановка
алгебраизирует тригонометрические
выражения следующим образом:
Пример.
.
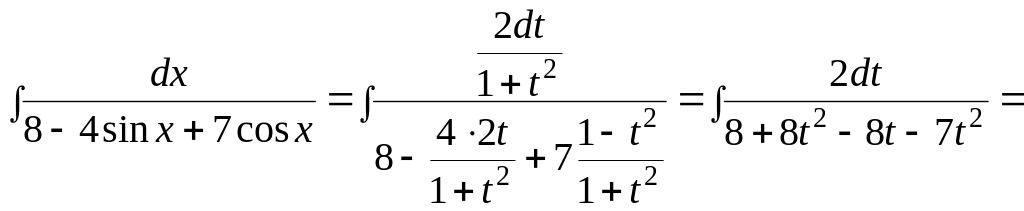
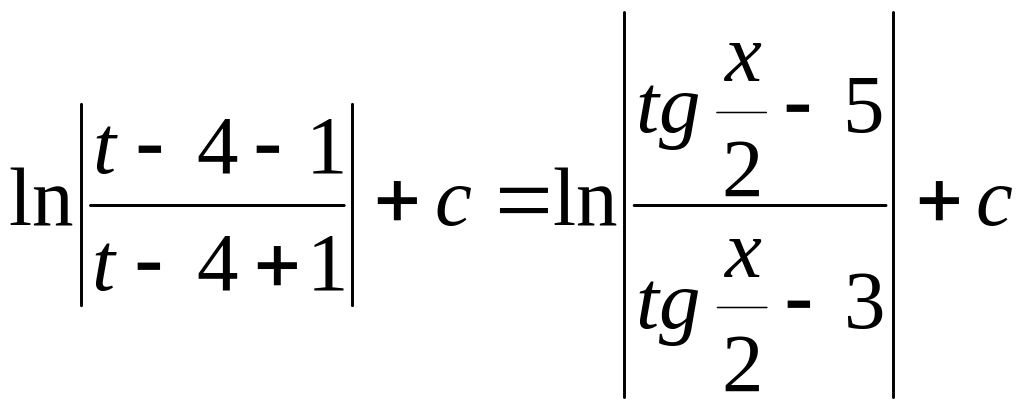При решении
интегралов вида
,
,
используются тригонометрические формулы
преобразующие
произведение тригонометрических функций в сумму.
Пример.
.
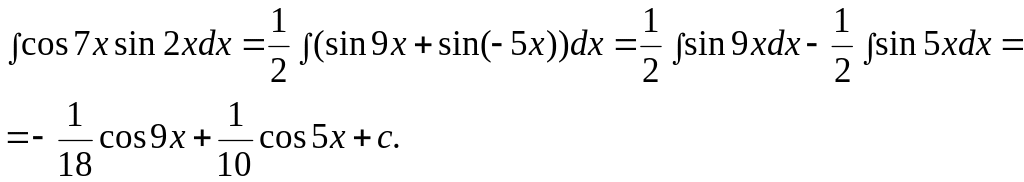Другие случаи, в которых используются алгебраические преобразования и тригонометрические формулы, а также замена переменной, рассмотрим на конкретных примерах.
Пример.
