3.3. Производные и дифференциалы высших порядков.

Пусть определена и дифференцируема на множестве , тогда сама является функцией от x и также может иметь производную.

Определение. Производной порядка функции называется производная от производной порядка, то есть .

Определение. Дифференциалом порядка функции называется дифференциал от дифференциала функции порядка, то есть

.

В частности

.

Замечание. Механический смысл второй производной состоит в том, что если точка движется прямолинейно по закону s=s(t), где s – путь, t – время, то представляет скорость изменения пути в момент , есть скорость изменения скорости или ускорение точки в момент .

Лекция 4. Основные теоремы дифференциального исчисления.

4.1. Теорема Ферма.

4.2. Теорема Ролля.

4.3. Теорема Лагранжа.

4.4. Теорема Коши.

4.5. Правило Лопиталя.

4.6.Формула Тейлора.

4.1. Теорема Ферма.

Теорема. Пусть функция определена на и в некоторой точке принимает наибольшее или наименьшее значение и дифференцируема в точке , тогда

Д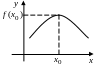 оказательство.

Для определенности положим, что в точке достигает наибольшего значения, то есть и . Тогда:

1) при и ;

2) при и

Из первого и второго следует, что .

Г еометрический смысл теоремы Ферма.

Касательная к графику функции в точках наибольшего и наименьшего значений параллельна оси абсцисс, если дифференцируема в этих точках.

4.2. Теорема Ролля.

Теорема.

Пусть функция непрерывна на , дифференцируема на и на концах отрезка в точках a и b принимает одинаковые значения , тогда , в которой .

Доказательство. Если , то , то есть в качестве точки c можно взять любую точку, принадлежащую .

Если не тождественна константе, то с учетом условия о непрерывности на по теореме Вейерштрасса можно утверждать, что принимает на этом отрезке наибольшее и наименьшее значения в точках и , у которых хотя бы одна попадёт внутрь . Пусть , . Так как функция дифференцируема на , то она дифференцируема в точке и по теореме Ферма , то есть в качестве точки c можно взять точку .

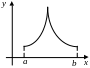
Геометрический смысл теоремы Ролля.

На найдется хотя бы одна точка, в которой касательная параллельна оси 0X.

Алгебраический смысл теоремы Ролля.

Между двумя последовательными корнями дифференцируемой функции

лежит хотя бы один корень её производной.

Замечание.

Все три требования теоремы Ролля существенны. При нарушении

х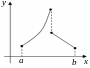 отя бы одного из них заключение теоремы может оказаться неверным.

4.3. Теорема Лагранжа.

Теорема.

Пусть функция непрерывна на и дифференцируема на , тогда существует точка такая, что .

Доказательство.

Введем вспомогательную функцию .

удовлетворяет всем условиям теоремы Ролля: непрерывна на , так как на непрерывны , и const;

дифференцируема на , так как на дифференцируемы , и const и существует ;

и .

Тогда по теореме Ролля на найдется точка c, в которой , то есть

.

Геометрический смысл.

Н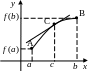 а интервале найдется хотя бы одна точка c, касательная в которой параллельна хорде, соединяющей точки и . Действительно. - угловой коэффициент касательной и - угловой коэффициент секущей. По теореме Лагранжа они равны, следовательно касательная параллельна секущей.