13.4. Линейные дифференциальные уравнения первого порядка.

Определение. Дифференциальное уравнение вида , где

, , - известные непрерывные на (а;в) функции, называется линейным дифференциальным уравнением первого порядка.

Это уравнение можно привести к виду (2) делением на , где . Это уравнение линейно, так как y и в первой степени. Если , то линейное уравнение называется однородным.

Рассмотрим способы решения уравнения (2).

Умножим обе части уравнения (2) на . Получим . Найдем производную функции , то есть = .

Проинтегрируем обе части последнего равенства: - общее решение уравнения (2).

Рассмотрим метод вариации произвольной постоянной на конкретном примере.

Пример. Решить уравнение .

Составим соответствующее однородное уравнение: .

Заменим и разделим переменные . Решение однородного уравнения: , то есть . Где с- постоянная. Общее решение исходного неоднородного уравнения будем искать в виде , где - неизвестная функция. Найдем или .

Подставим выражения для y и в исходное уравнение, тогда

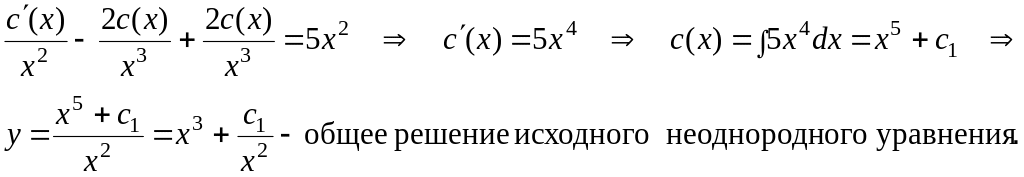
Следует отметить, что некоторые нелинейные уравнения приводятся к линейным соответствующими заменами неизвестных функций . К таковым относится уравнение Бернулли: , где p и g - непрерывные функции, . Для его решения вводят новую функцию и получают линейное дифференциальное неоднородное уравнение относительно функции : (2).

Пример. Если , то, согласно (2), имеем .

13.5. Однородные дифференциальные уравнения первого порядка.

Для рассмотрения однородных дифференциальных уравнений первого порядка введем понятие однородных функций.

Определение. Функция называется однородной n-го измерения по своим переменным х и у, если она удовлетворяет равенству .

Замечания:

1) Однородная функция нулевого измерения фактически зависит от отношения , так как, если в соотношении считать , то .

2) Отношение двух однородных функций одного и того же измерения

является однородной функцией нулевого измерения.

Пусть , где и однородные функции n-го измерения, то есть , тогда .

Определение. Однородным дифференциальным уравнением первого порядка называется уравнение вида (3), правая часть которого является однородной функцией нулевого измерения, то есть .

Для решения однородного уравнения используется подстановка , где - неизвестная функция и = , или . Подставим выражения у и в уравнение , получим (*) - уравнение с разделяющимися переменными. Так как , то и = - уравнение с разделенными переменными. Интегрируя последнее уравнение получим - общий интеграл уравнения (*).

После нахождения необходимо вернуться к функции и найти общий интеграл уравнения (3).

Замечания.

1. Уравнение является однородным, если правая часть:

1) зависит фактически от отношения ;

2) является отношением двух однородных функций одного измерения.

2. Уравнение вида является однородным, если P(x) и Q(y) - однородные функции одного измерения.

Пример. Решить уравнение .

Решение. . Так как , то . Так как , то ,

= , , .

Так как , то - общее решение уравнения.