16.5. Разложение элементарных функций в степенные ряды.

Запишем ряд Тейлора для функции :

.

1) Рассмотрим функцию

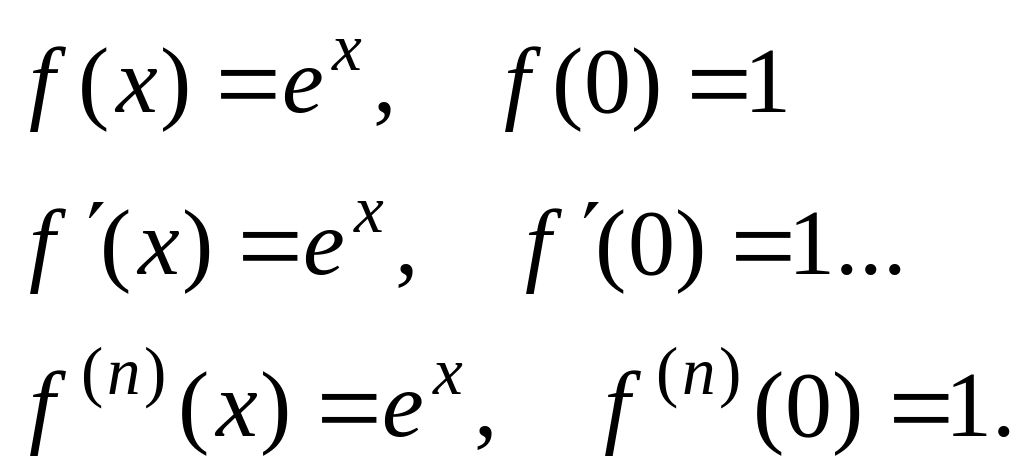Тогда

2) Для функции

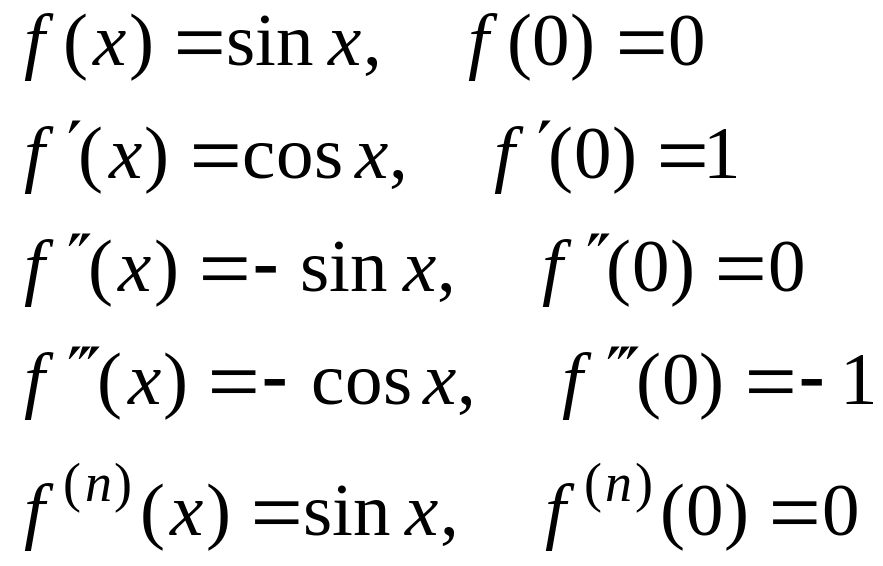Нечётная функция у= sinx разлагается в ряд по нечётным степеням х:

3) Ряд для cosx получим почленным дифференцированием ряда sinx:

4) Для функции у= разложение в ряд имеет вид:

5) Для функции получим разложение в степенной ряд почленно

интегрируя ряд , тогда

=

= , область сходимости этого ряда

Раздел VIII.

Экономико-математические модели.

В этом разделе рассматриваются простейшие приложения высшей математики в экономике, которые рассчитаны на уровень подготовки студентов первого курса и почти не требуют дополнительной экономической информации.

Лекция 17. Модели межотраслевого баланса.

17.1. Статическая модель межотраслевого баланса – модель Леонтьева.

17.2. Динамическая модель межотраслевого баланса.

17.3. Линейная модель торговли.

17.1. Статическая модель межотраслевого баланса – модель Леонтьева.

Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль с одной стороны, является производителем, а с другой – потребителем продукции, выпускаемой другими отраслями. Возникает довольно непростая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 году в трудах известного американского экономиста В.В. Леонтьева, который попытался проанализировать причины экономической депрессии США 1929 – 1932 гг. Эта модель основана на алгебре матриц и использует аппарат матричного исчисления.

Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.

Рассмотрим процесс производства за некоторый период времени (например, год).

Введем обозначения:

X_i – общий (валовой) объем продукции i-й отрасли (i= );

X_ij – объем продукции i-й отрасли, потребляемый j-й отраслью в процессе производства (i,j= );

Y_i – объем конечного продукта i-й отрасли для непроизводственного потребления (i= ).

Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i-й отрасли должен быть равным сумме объемов потребления в производственной и внепроизводственной сферах:

(i= ) (1)

Уравнения (1) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1), имеют стоимостное выражение.

Введем коэффициенты прямых затрат (i,j= ), показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли. Можно считать, что в некотором промежутке времени коэффициенты будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, то есть (i,j= ), вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Соотношения баланса теперь примут вид , (i= ) (2). Обозначим

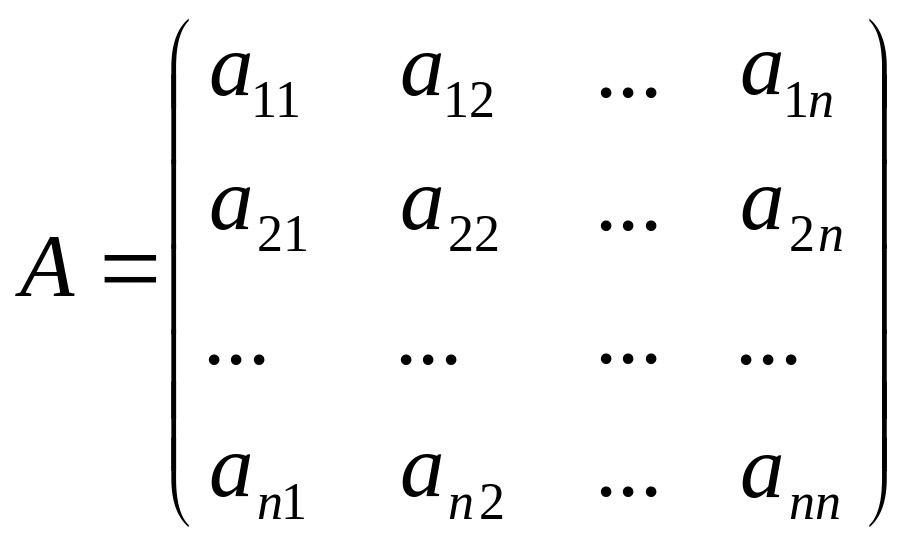, , , где X – вектор валового выпуска, Y – вектор конечного продукта, A - матрица прямых затрат.

Систему (2) можно записать в матричной форме (3)

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.

Перепишем уравнение (3) в виде: (4). Если , то - решение уравнения (3). Матрица называется матрицей полных затрат, каждый элемент которой является величиной валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли .

В соответствии с экономическим смыслом задачи значения при и .

Матрица называется продуктивной, если для любого вектора существует решение матричного уравнения (4).

Теорема (Критерий продуктивности матрицы).

Для того, чтобы матрица A была продуктивна, необходимо и достаточно, чтобы: 1) для любых ; 2) для любого ; 3)существует номер .

Пример.

В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.

Отрасль		Потребление		Конечный продукт	Валовой выпуск
		Энергетика	Машиностроение
Производство	Энергетика	14	42	144	200
	Машиностроение	24	30	246	300

Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится в 1,2 раза, а машиностроительной останется на прежнем уровне.

Решение.

Составим матрицу A прямых затрат 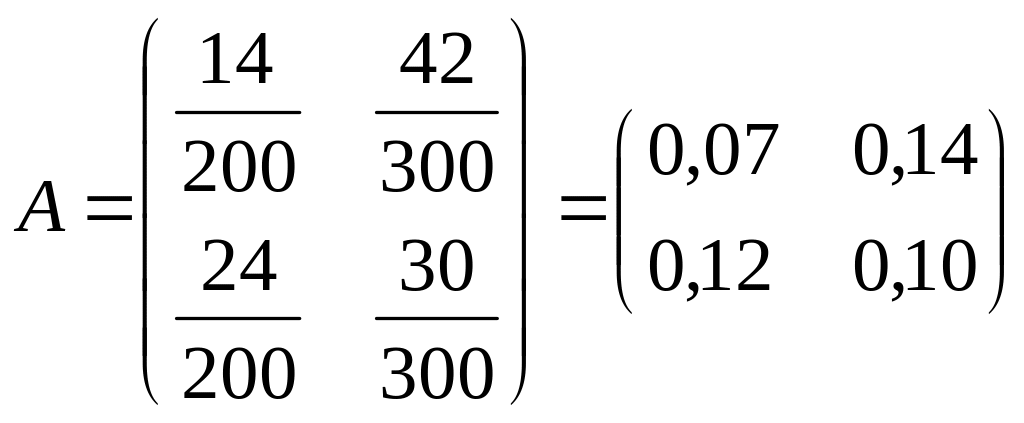, она имеет неотрицательные элементы и удовлетворяет критерию продуктивности: 0,07+0,12=0,19<1; 0,14+0,10=0,24 .

Для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска .

Найдем матрицу полных затрат .

, , .

По условию вектор конечного продукта , тогда , то есть валовой выпуск в энергетической отрасли надо увеличить до 314,56 усл. ед., а в машиностроительной – до 364,30 усл. ед..